Рассмотрим нелинейную задачу для дифференциального уравнения первого порядка, не разрешенного относительно производной
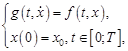(1)
где функции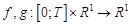 
и предполагается, что функция 
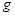непрерывна, функция 
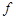удовлетворяет условию Каратеодори.
Пусть 
– пространство суммируемых в степени 
на отрезке 
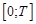функций, 
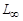– пространство измеримых ограниченных в существенном на отрезке 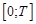функций, 
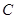- пространство непрерывных на отрезке 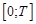функций, 
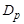- пространство абсолютно непрерывных на отрезке 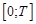функций с нормой: 
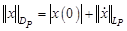. Под решением понимается такой элемент пространства 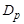, который почти всюду на отрезке 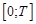удовлетворяет уравнению и начальному условию задачи (1).
В работе доказывается существование решения задачи (1) в шаре радиуса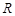 
с центром в точке 
пространства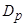 
. С помощью метода явной линеаризации задача (1) сводится к квазилинейной задаче с обратимым линейным оператором. В последующем, полученная задача заменяется эквивалентным ей операторным уравнением, к которому применяется теорема типа Лере-Шаудера [10]. При этом решение задачи (1) ищется в предположении, что существует функция 
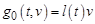, удовлетворяющая условию: для каждого фиксированного 
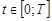на искомом шаре с центром в точке пространства 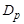выполняется неравенство
.
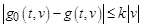Случай задачи (1) с периодическим краевым условием рассматривался ранее в работе [6].
Некоторые математические модели реальных процессов приводят к задачам для обыкновенных дифференциальных уравнений, не разрешенных относительно старшей производной и, в частности, к задаче (1). Обычно при исследовании нелинейных задач, в том числе и задачи (1), используется явная или неявная линеаризация. В частности, в работах [3,5,8] используется редукция нелинейной задачи к некоторой вспомогательной квазилинейной, к которой применяются известные схемы исследования на разрешимость квазилинейных или резонансных краевых задач. К числу методов, использующих неявную линеаризацию нелинейных задач можно отнести метод Ньютона-Канторовича, метод применения теорем о неявной функции, методы теории нелинейных фредгольмовых операторов. В этом случае нелинейный оператор аппроксимируется своей производной [1,2,4].
Обозначим через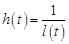 
, при этом будем предполагать, что функции 
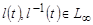на отрезке 
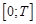. Существование такой функции позволяет задачу (1) переписать в виде
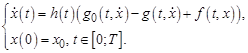(2)
Обозначим через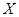 
и 
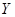пространства 
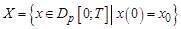и 
соответственно. Задачу (2) в пространстве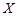 
запишем в виде операторного уравнения
,
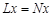где операторы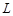 
,
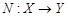определены равенствами
, 
,
.
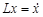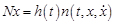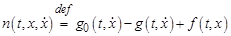Так как оператор 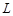является обратимым на пространстве 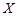, то краевая задача (2) эквивалентна интегральному уравнению
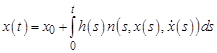. (3)
Соответствующее операторное уравнение тогда запишется в виде
,
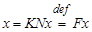где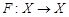
, 
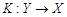- обратный к 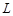оператор.
Ниже под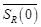 
и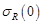 
понимается замкнутый шар и сфера радиусов 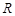с центрами в нуле.
Для нахождения условий существования решения уравнения (3) воспользуемся теоремой типа Лере – Шаудера [10] из книги [9, стр.406]:
Теорема 1. Пусть оператор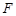 
действует из шара 
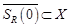в 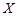и вполне непрерывен. Если 
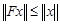для всех 
с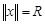 
, то оператор 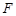имеет в 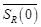неподвижную точку.
Для доказательства полной непрерывности произведения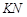 
рассмотрим расширение оператора 
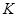на пространство 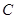, то есть будем считать, что оператор 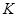действует из пространства в 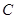. Тогда оператор 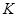вполне непрерывен, а, следовательно, произведение 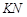также вполне непрерывно. Не трудно показать, что 
.
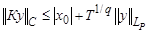Докажем существование решения уравнения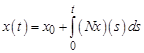 
на пространстве 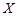, содержащегося в пространстве 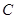. Тогда, вследствие непрерывности оператора 
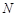, правая часть данного уравнения принадлежит 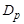и, следовательно, само решение 
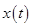также принадлежит 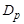. Это доказывает существование решения исходной задачи (1) в пространстве 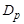. Подобный подход использовался в работе [7].
Для нахождения эффективных условий разрешимости, ценим оператор 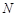в уравнении (3):
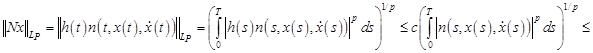
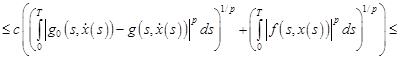
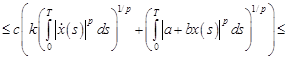
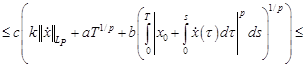
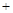
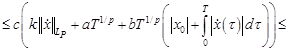
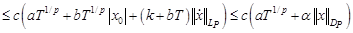
(где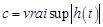 
, 
).
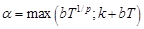Так как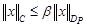 
, где 
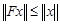, то условие Теоремы 1: для всех с 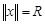, примет вид
.
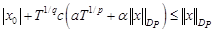Из данного неравенства находим радиус шара 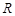, на котором существует решение уравнения (3):
.
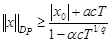Откуда следует, что если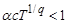 
, то на сфере 
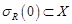радиуса 
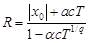выполнены условия теоремы 1.
Таким образом, доказано утверждение о существовании решения краевой задачи (1):
Теорема 2. Пусть функция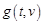 
непрерывна, функция 
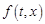удовлетворяет условию Каратеодори и существует функция 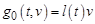(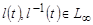), удовлетворяющая условию:
для каждого фиксированного 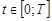выполняется неравенство
.
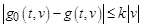Тогда если выполнены условия
1)
;
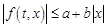2) ,
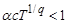где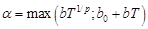 
, 
, 
,
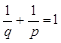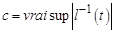то существует решение задачи (1) на шаре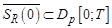 
с радиусом .
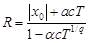Библиографическая ссылка
Колпаков И.Ю., Ефимов Н.А., Юдин Р.Ю. О ЗАДАЧЕ КОШИ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, НЕ РАЗРЕШЕННОГО ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ // Международный студенческий научный вестник. – 2017. – № 5. ;URL: https://eduherald.ru/ru/article/view?id=17798 (дата обращения: 19.04.2024).