Рассмотрим нелинейную задачу для дифференциального уравнения первого порядка, не разрешенного относительно производной
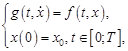 (1)
(1)
где функции 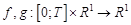 и предполагается, что функция
и предполагается, что функция 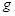 непрерывна, функция
непрерывна, функция 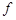 удовлетворяет условию Каратеодори.
удовлетворяет условию Каратеодори.
Пусть  – пространство суммируемых в степени
– пространство суммируемых в степени  на отрезке
на отрезке 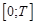 функций,
функций,  – пространство измеримых ограниченных в существенном на отрезке
– пространство измеримых ограниченных в существенном на отрезке 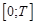 функций,
функций, 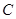 - пространство непрерывных на отрезке
- пространство непрерывных на отрезке 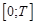 функций,
функций, 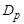 - пространство абсолютно непрерывных на отрезке
- пространство абсолютно непрерывных на отрезке 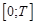 функций с нормой:
функций с нормой: 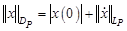 . Под решением понимается такой элемент пространства
. Под решением понимается такой элемент пространства 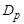 , который почти всюду на отрезке
, который почти всюду на отрезке 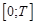 удовлетворяет уравнению и начальному условию задачи (1).
удовлетворяет уравнению и начальному условию задачи (1).
В работе доказывается существование решения задачи (1) в шаре радиуса 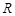 с центром в точке
с центром в точке  пространства
пространства 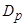 . С помощью метода явной линеаризации задача (1) сводится к квазилинейной задаче с обратимым линейным оператором. В последующем, полученная задача заменяется эквивалентным ей операторным уравнением, к которому применяется теорема типа Лере-Шаудера [10]. При этом решение задачи (1) ищется в предположении, что существует функция
. С помощью метода явной линеаризации задача (1) сводится к квазилинейной задаче с обратимым линейным оператором. В последующем, полученная задача заменяется эквивалентным ей операторным уравнением, к которому применяется теорема типа Лере-Шаудера [10]. При этом решение задачи (1) ищется в предположении, что существует функция 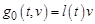 , удовлетворяющая условию: для каждого фиксированного
, удовлетворяющая условию: для каждого фиксированного 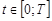 на искомом шаре с центром в точке
на искомом шаре с центром в точке  пространства
пространства 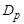 выполняется неравенство
выполняется неравенство
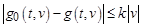 .
.
Случай задачи (1) с периодическим краевым условием рассматривался ранее в работе [6].
Некоторые математические модели реальных процессов приводят к задачам для обыкновенных дифференциальных уравнений, не разрешенных относительно старшей производной и, в частности, к задаче (1). Обычно при исследовании нелинейных задач, в том числе и задачи (1), используется явная или неявная линеаризация. В частности, в работах [3,5,8] используется редукция нелинейной задачи к некоторой вспомогательной квазилинейной, к которой применяются известные схемы исследования на разрешимость квазилинейных или резонансных краевых задач. К числу методов, использующих неявную линеаризацию нелинейных задач можно отнести метод Ньютона-Канторовича, метод применения теорем о неявной функции, методы теории нелинейных фредгольмовых операторов. В этом случае нелинейный оператор аппроксимируется своей производной [1,2,4].
Обозначим через 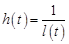 , при этом будем предполагать, что функции
, при этом будем предполагать, что функции 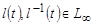 на отрезке
на отрезке 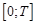 . Существование такой функции позволяет задачу (1) переписать в виде
. Существование такой функции позволяет задачу (1) переписать в виде
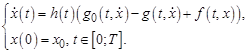 (2)
(2)
Обозначим через 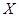 и
и  пространства
пространства  и
и  соответственно. Задачу (2) в пространстве
соответственно. Задачу (2) в пространстве 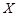 запишем в виде операторного уравнения
запишем в виде операторного уравнения
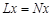 ,
,
где операторы 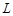 ,
,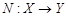 определены равенствами
определены равенствами
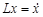 ,
, 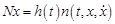 ,
,
 .
.
Так как оператор 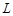 является обратимым на пространстве
является обратимым на пространстве 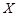 , то краевая задача (2) эквивалентна интегральному уравнению
, то краевая задача (2) эквивалентна интегральному уравнению
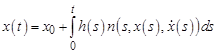 . (3)
. (3)
Соответствующее операторное уравнение тогда запишется в виде
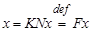 ,
,
где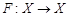 ,
, 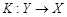 - обратный к
- обратный к 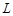 оператор.
оператор.
Ниже под 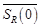 и
и 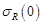 понимается замкнутый шар и сфера радиусов
понимается замкнутый шар и сфера радиусов 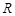 с центрами в нуле.
с центрами в нуле.
Для нахождения условий существования решения уравнения (3) воспользуемся теоремой типа Лере – Шаудера [10] из книги [9, стр.406]:
Теорема 1. Пусть оператор 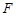 действует из шара
действует из шара 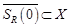 в
в 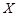 и вполне непрерывен. Если
и вполне непрерывен. Если 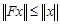 для всех
для всех  с
с 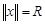 , то оператор
, то оператор 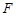 имеет в
имеет в 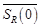 неподвижную точку.
неподвижную точку.
Для доказательства полной непрерывности произведения  рассмотрим расширение оператора
рассмотрим расширение оператора  на пространство
на пространство 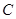 , то есть будем считать, что оператор
, то есть будем считать, что оператор  действует из пространства
действует из пространства  в
в 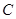 . Тогда оператор
. Тогда оператор  вполне непрерывен, а, следовательно, произведение
вполне непрерывен, а, следовательно, произведение  также вполне непрерывно. Не трудно показать, что
также вполне непрерывно. Не трудно показать, что 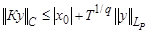 .
.
Докажем существование решения уравнения 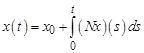 на пространстве
на пространстве 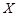 , содержащегося в пространстве
, содержащегося в пространстве 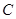 . Тогда, вследствие непрерывности оператора
. Тогда, вследствие непрерывности оператора 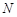 , правая часть данного уравнения принадлежит
, правая часть данного уравнения принадлежит 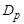 и, следовательно, само решение
и, следовательно, само решение 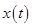 также принадлежит
также принадлежит 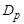 . Это доказывает существование решения исходной задачи (1) в пространстве
. Это доказывает существование решения исходной задачи (1) в пространстве 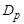 . Подобный подход использовался в работе [7].
. Подобный подход использовался в работе [7].
Для нахождения эффективных условий разрешимости, ценим оператор 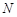 в уравнении (3):
в уравнении (3):
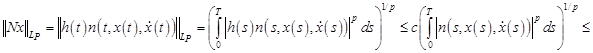
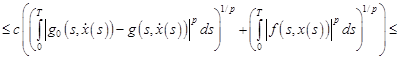
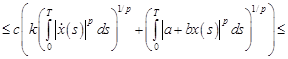
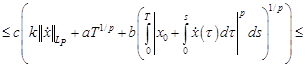
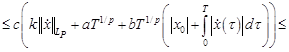
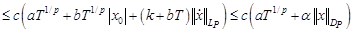
(где  ,
, 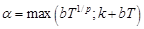 ).
).
Так как  , где
, где  , то условие Теоремы 1:
, то условие Теоремы 1: 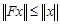 для всех
для всех  с
с 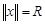 , примет вид
, примет вид
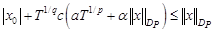 .
.
Из данного неравенства находим радиус шара 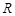 , на котором существует решение уравнения (3):
, на котором существует решение уравнения (3):
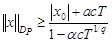 .
.
Откуда следует, что если 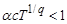 , то на сфере
, то на сфере 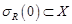 радиуса
радиуса  выполнены условия теоремы 1.
выполнены условия теоремы 1.
Таким образом, доказано утверждение о существовании решения краевой задачи (1):
Теорема 2. Пусть функция  непрерывна, функция
непрерывна, функция 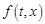 удовлетворяет условию Каратеодори и существует функция
удовлетворяет условию Каратеодори и существует функция 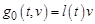 (
(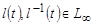 ), удовлетворяющая условию:
), удовлетворяющая условию:
для каждого фиксированного 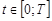 выполняется неравенство
выполняется неравенство
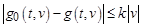 .
.
Тогда если выполнены условия
1)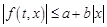 ;
;
2) 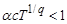 ,
,
где  ,
, 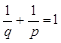 ,
, 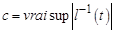 ,
,
то существует решение задачи (1) на шаре 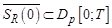 с радиусом
с радиусом  .
.

