По поводу вопроса о численном решении уравнений и их систем глобальная сеть Интернет, а именно Википедия, утверждает, что оно «состоит в приближённом определении корней уравнения или системы уравнений и применяется в случаях, когда точный метод решения неизвестен или трудоёмок» ([5]). Необходимость в численном решении уравнений может возникнуть у будущих инженеров электроэнергетиков и электротехников во время выполнения ими служебных обязанностей, поэтому так важно обучающимся знать методы решения подобных уравнений и систем, а также возможности их решения в математических средах, к примеру, MathCAD. Сузим вопрос до численного решения уравнений, точнее, нахождение корней заданной непрерывной на некотором интервале функции.
Численные методы решения уравнений (алгебраических, трансцендентных) достаточно глубоко проработаны и известны. Укажем наиболее простые и употребительные с точки зрения изучения их в высшей школе: метод Ньютона (метод касательных), метод хорд, комбинированный метод, метод итераций. Практически все эти методы используют принцип сжимающих отображений (Теорема Банаха), знать который обязаны все студенты энергетики.
В настоящей статье рассмотрим итерационный метод, который также использует принцип сжимающих отображений.
Нашей задачей мы считаем включение указанных методов вычисления корней уравнений в информационную образовательную среду (ИОС) кафедры в виде интерактивного обучающего документа ([1], [2]). Решения примеров, включаемых в документ, известны и стандартны, но методический подход к изучению методов и способов решения, включаемых в электронный документ носит элемент новизны.
В интерактивный обучающий документ помещается теория и примеры решения задач. Так, например, в документе обязательно будет пояснение проблемы нахождения корней функции.
Решая уравнение вида
f(x) = 0,
где f(x) определена и непрерывна на некотором конечном или бесконечном интервале a lt; x lt; b, мы практически решаем следующие задачи:
1) отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен только один корень уравнения (так называемый изолированный корень);
2) вычисление корней с заданной точностью.
Отделение корней будем осуществлять графическим способом. Вычисление же корней будем проводить с помощью указанных выше методов.
Итерационный метод является, по сути, методом последовательных приближений или методом простой итерации. Скорость сходимости метода довольна низка, при этом высока наглядность происходящего процесса поиска корней, поэтому мы так подробно на нём останавливаемся. Тем более что обучающиеся могут самостоятельно подготавливать интерактивный обучающий документ, встраивать новое содержание (новое условие) в документ, добавлять информацию.
В качестве примера рассмотрим следующий фрагмент интерактивного обучающего документа.
Вычислить численными методами корни функции: f(x) = x2 – 3x + 2.
Довольно часто можно встретить решение подобных примеров в виде последовательных рассуждений с достаточно большим количеством повторений – до тех пор, пока не выполнится поставленное в задаче условие окончания вычислений. Наша цель максимально автоматизировать процесс вычисления корней функции с заданной степенью точности. Решение можно выполнить в любой вычислительной среде, например, Excel, MathCAD, Mathematika.
Решим поставленную задачу в математической среде MathCAD методом половинного деления. Обучающиеся под руководством преподавателя составляют в математической среде MathCAD программу (функцию пользователя). Программа даёт полностью автоматизированное вычисление корня для любой заданной непрерывной функции. Но сначала на экран выводится значение корней заданной функции с помощью встроенной в математическую среду процедуры root. Далее для получения грубого приближения корня строится график заданной функции. В примере ниже задана функция, имеющая точные корни в точках 1 и 2 по оси х. По этой причине мы сможем установить насколько точно работает составленная нами программа (функция пользователя).
Вначале задаётся сама функция. Затем строится её график (рисунок).
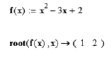
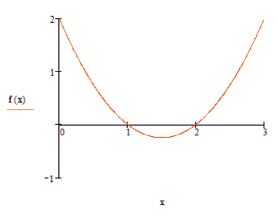
График функции в среде MathCAD
Учитывая сказанное выше (задана простая функция), решение максимально понятно, а результат – может быть легко проинтерпретирован. Процедура (или функция) root, заданная с параметрами, и график дают два известных корня функции соответствующих ручным вычислениям. Далее составляем функцию пользователя с учётом точности вычислений и отрезка, на котором ищется корень. Даже при первом взгляде на программу сразу становится заметным насколько просто и очевидно решение. Несколько сложнее будут выглядеть решения для методов Ньютона (метод касательных), хорд, комбинированного метода.
Очевидно, что вычислительный процесс продолжается только с такими значениями концов отрезка, в которых значения функции получаются разных знаков. При желании в данную функцию пользователя легко встроить счётчик проведённых итераций. Понятно, что чем сложнее метод вычисления корней функции, тем быстрее будет найден результат.
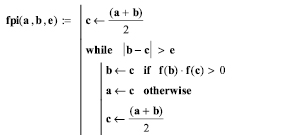
Подошло время опробовать нашу программу.
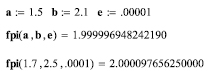
Найден только второй из корней. Полученный результат можно проинтерпретировать следующим образом: при заданной точности вычислений количество верных цифр результата соответствует этой точности. Округление как раз и даст требуемый (уже известный нам) результат. При необходимости, задав другие значения для интервала поиска, можем получить и первый корень.
Приведём формулы других методов вычисления корней функции.
1) Метод хорд. Если выполняются соответствующие условия, то левый конец интервала не движется и формула принимает вид:
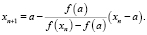
2) Метод касательных. Формула принимает вид:
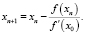
3) Комбинированный метод. Заключается в том, что применяются обе указанные выше формулы, при этом при выполнении соответствующих условий по одной из формул будет вычисляться корень по недостатку, по другой – по избытку.
Для того чтобы применять приведённые выше методы вычисления корней функции, студент должен уверенно ориентироваться в теоретическом материале. Указанная тема одна из самых трудных в численных методах. Поэтому без каких-либо усилий, без самостоятельной работы над учебным материалом данная тема «пройдёт» мимо студента. Как следствие, только подготовка интерактивного обучающего документа по изучению вопроса может помочь студенту освоить численные методы.
Студенты работают с данным интерактивным обучающим документом с большим интересом, т.к. такой сложный вопрос, как поиск корней уравнения, решается так просто, очевидно и понятно, да ещё и с использованием компьютера. Учебный процесс и самоподготовка с подобным интерактивным обучающим документом проходит в активной и интерактивной формах ([4], [3]), мотивирует обучающихся принимать участие в подготовке аналогичных учебных материалов.
Библиографическая ссылка
Садков К.О., Часов К.В. ИССЛЕДОВАНИЕ ЧИСЛЕННОГО РЕШЕНИЯ УРАВНЕНИЙ В ИНФОРМАЦИОННОЙ ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ // Международный студенческий научный вестник. 2017. № 4-6. ;URL: https://eduherald.ru/ru/article/view?id=17569 (дата обращения: 09.04.2025).

