1
Темирбулатова М.О.
1
Магомедова Э.Г.
1
1 ФГБОУ ВО «Ставропольский государственный аграрный университет»
Применение статистических методов обработки данных стало общепринятым и широко распространенным в финансовой сфере, в том числе в банковской деятельности, страховании, инвестировании. В статье рассматриваются особенности использования методов математической статистики в инвестиционной деятельности. Изучено их применение на основе оценки рисков инвестирования с помощью использования дисперсии доходности. Проанализировано применение выборочной и генеральной совокупности при оценке дисперсии. Для наглядного представления произведена оценка рисков приобретения акций двух условных компаний АО «ПРОМСТРОЙМЕТАЛЛ» и АО «АРМСТИЛЬКАМПАНИ». Использовано графическое представление в виде многоугольника распределения. Рассчитана ожидаемая доходность акций обеих компаний и их дисперсии и на основе сравнительного анализа обнаружено, что риски инвестирования в АО «ПРОМСТРОЙМЕТАЛЛ» при практически одинаковой ожидаемой доходности. Таким образом, в статье рассмотрены теоретические аспекты применения методов математической статистики и на примере рассмотрено их практическое применение.
математическая статистика
оценка рисков инвестирования
дисперсия доходности
ожидаемая ценность актива
1. Гулай Т.А., Литвин Д.Б., Долгополова А. Ф. Использование математических методов для анализа динамических свойств управляемого объекта // Моделирование производственных процессов и развитие информационных систем. 2012. С. 167–170.
2. Долгополова А.Ф., Гулай Т.А., Литвин Д. Б. Математическое моделирование социально-экономических систем // Учетно-аналитические и финансово-экономические проблемы развития региона : Ежегодная 76-я науч.-практ. конф. СтГАУ «Аграрная наука – Северо-Кавказскому региону». 2012. С. 283–286.
3. Гулай Т.А., Долгополова А.Ф., Литвин Д. Б. Личностно-ориентированное обучение математике студентов экономических направлений как средство повышения качества обучения // Теоретические и прикладные проблемы современной педагогики. 2012. С. 28–33.
4. Субоптимальное оценивание вектора угловой скорости объекта по измерениям распределенной акселерометрической системы / Д. Б. Литвин, А. Н. Хабаров, И. П. Шепеть, В. Г. Бондарев, Е. В. Озеров. Вестник АПК Ставрополья. 2013. № 3 (11). С. 60–63.
5. Литвин Д.Б., Гулай Т.А., Долгополова А. Ф. Применение операционного исчисления в моделировании экономических систем // Аграрная наука, творчество, рост. 2013. С. 263–265.
6. Литвин Д. Б., Гулай Т. А., Долгополова А. Ф. Коррекция динамического диапазона статистических данных // Статистика вчера, сегодня, завтра : Междунар. научно-практ. конф., посвященная 155-летию образования Ставропольского губернского комитета статистики, 150-летию образования в России Центрального статистического комитета и Международному году статистики. 2013. С. 148–152.
7. Метод повышения точности измерения векторных величин / Д. В. Бондаренко, С. М. Бражнев, Д. Б. Литвин, А.А. Варнавский. НаукаПарк. 2013. № 6 (16). С. 66–69.
8. Долгополова А.Ф., Гулай Т.А., Литвин Д. Б. Совершенствование экономических механизмов для решения проблем экологической безопасности // Информационные системы и технологии как фактор развития экономики региона: II Междунар. науч.-практ. конф. 2013. С. 68–71.
9. Литвин Д. Б., Шепеть И. П. Моделирование роста производства с учетом инвестиций и выбытием фондов // Социально-экономические и информационные проблемы устойчивого развития региона: Междунар. науч.-практ. конф. 2015. С. 114–116.
10. Litvin D., Ghazwan R Q. Thinking skills product in mathematics among the students of the university // Экономические, инновационные и информационные проблемы развития региона. : материалы Междунар. науч.-практ. конф. 2014. С. 5–9.
11. Устройство для решения дифференциальных уравнений / И. П. Шепеть, С. М. Бражнев, Д. Б. Литвин, Е. Д. Литвина, А. В. Захарин, С. В. Слесаренок патент на изобретение RUS 2538945 26.12.2013.
12. Литвин Д. Б., Таволжанская О. Н. Элементы математической статистики : учебное пособие. Ставрополь, 2015.
13. Litvin D. B. Mathematical self-concept among university students // Аграрная наука, творчество, рост : сб. науч. тр. по материалам IV Междунар. науч.-практ. конф. 2014. С. 326–329.
14. Применение дифференциального исчисления функций нескольких переменных к разработке алгоритма определения координат объекта / Д. Б. Литвин, И. П. Шепеть, В. Г. Бондарев, Е. Д. Литвина // Финансово-экономические и учетно-аналитические проблемы развития региона : материалы Ежегодной 78-й науч.-практ. конф. 2014. С. 242–246.
15. Литвин Д. Б., Дроздова Е. А. Математическое моделирование в среде визуального программирования. Современные наукоемкие технологии. 2013. № 6. С. 77–78.
В современном мире уделяется все большее внимание использованию математических методов в различных сферах экономики. Применение статистических методов обработки данных стало общепринятым и широко распространенным в финансовой сфере, в том числе в банковской деятельности, страховании, инвестировании [6, 10]. Использование различных статистических методов анализа данных, в первую очередь их точечных оценок – математического ожидания и дисперсии – позволяет грамотно управлять финансовыми рисками, осуществлять банковский менеджмент и другие виды деятельности [5, 12].
Рассмотрим применение методов математической статистики на основе оценки рисков инвестирования. В портфельной теории меры риска, связанные с инвестированием в определенный актив или портфель активов, рассчитываются с использованием дисперсии доходности. В математической статистике дисперсия является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания [7, 11].
Если известен полный набор вероятностей исхода события, что достаточно редко встречается на практике, для расчета величины дисперсии используется следующая формула:
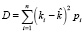
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;
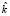 – ожидаемая доходность ценной бумаги или актива;
– ожидаемая доходность ценной бумаги или актива;
pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования финансовый аналитик обычно располагает статистическими данными о доходности ценной бумаги или актива [1,14]. Если ему доступен весь массив информации, то есть он оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
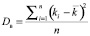
где ki – i-ое значение доходности ценной бумаги;
n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1 [4, 15]. В этом случае формула для ее оценки будет выглядеть следующим образом:
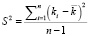
Полученное значение дисперсии характеризует разброс доходности актива или портфеля активов относительно его ожидаемой доходности [9]. Чем больше значение дисперсии, тем выше будет уровень риска. И напротив, низкие значения характеризуют низкий уровень рисков, связанных с осуществлением инвестиций [2, 8].
Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций АО «ПРОМСТРОЙМЕТАЛЛ» и АО «АРМСТИЛЬКАМПАНИ». Предположим, что известен полный набор случайных событий – доходностей с соответствующими им вероятностями, который представлен в таблице.
|
Варианты
|
1
|
2
|
3
|
4
|
5
|
|
АО «ПРОМСТРОЙМЕТАЛЛ»
|
|
ki %
|
5
|
12
|
23
|
33
|
51
|
|
pi
|
0,07
|
0,4
|
0,13
|
0,3
|
0,1
|
|
АО «АРМСТИЛЬКАМПАНИ»
|
|
ki %
|
-11
|
-5
|
20
|
35
|
58
|
|
pi
|
0,07
|
0,4
|
0,13
|
0,3
|
0,1
|
Изобразим многоугольники распределения, которые дадут приближенное наглядное представление о характере распределения случайной величины. На оси абсцисс отложим доходности активов при i-ом варианте исхода событий, а на оси ординат вероятности i-го варианта исхода событий.
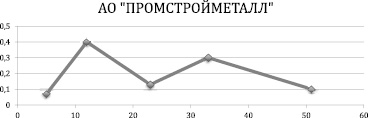
Рис. 1. Многоугольник распределения для АО «ПРОМСТРОЙМЕТАЛЛ»
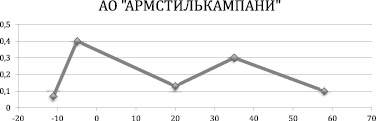
Рис. 2. Многоугольник распределения для АО «АРМСТИЛЬКАМПАНИ»
Ожидаемая доходность для акций АО «ПРОМСТРОЙМЕТАЛЛ» составит 23,14 %, а для акций АО «АРМСТИЛЬКАМПАНИ»16,13 %.
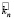 = 5*0,07 + 12*0,4 + 23*0,13 +
= 5*0,07 + 12*0,4 + 23*0,13 +
+ 33*0,3 + 51*0,1 = 23,14 %
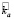 = (-11)*0,07-5*0,4 +
= (-11)*0,07-5*0,4 +
+ 20*0,13 + 35*0,3 + 58*0,1 = 16,13 %
В свою очередь, дисперсия доходности акций АО «ПРОМСТРОЙМЕТАЛЛ» будет равна 179,46 %, а акций АО «АРМСТИЛЬКАМПАНИ» 514,19 %
D = (5 – 23,14)2*0,07 + (12 – 23,14)2*0,4 +
+ (23 – 23,14)2*0,13 +
(33 – 23,14)2*0,3 +(51 – 23,14)2*0,1 = 179,46 %
D = ((-11)-16,13)20,07 + ((-5)-16,13)2*0,4 +
+ (20-16,13)2*0,13 + (35-16,13)2*0,3 +
+ (58-16,13)2*0,1 = 514,19 %.
Хотя ожидаемая доходность акций компаний отличается незначительно, риски инвестирования в акции АО «АРМСТИЛЬКАМПАНИ будут существенно выше.
Рассмотрев применение методов математической статистики на примере оценки доходности активов и оценки рисков инвестирования в них, мы убедились в практической значимости математической статистики как науки и необходимости ее изучения для дальнейшего использования в различных сферах деятельности, в том числе и финансовой сфере [3, 13].
Библиографическая ссылка
Темирбулатова М.О., Магомедова Э.Г. МЕТОДИКА КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ИНВЕСТИЦИОННЫХ РИСКОВ // Международный студенческий научный вестник. 2017. № 4-4.
;
URL: https://eduherald.ru/ru/article/view?id=17439 (дата обращения: 04.04.2025).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
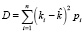
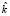 – ожидаемая доходность ценной бумаги или актива;
– ожидаемая доходность ценной бумаги или актива;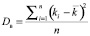
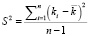


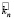 = 5*0,07 + 12*0,4 + 23*0,13 +
= 5*0,07 + 12*0,4 + 23*0,13 + 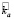 = (-11)*0,07-5*0,4 +
= (-11)*0,07-5*0,4 + 
