В современном мире уделяется все большее внимание использованию математических методов в различных сферах экономики. Применение статистических методов обработки данных стало общепринятым и широко распространенным в финансовой сфере, в том числе в банковской деятельности, страховании, инвестировании [6, 10]. Использование различных статистических методов анализа данных, в первую очередь их точечных оценок – математического ожидания и дисперсии – позволяет грамотно управлять финансовыми рисками, осуществлять банковский менеджмент и другие виды деятельности [5, 12].
Рассмотрим применение методов математической статистики на основе оценки рисков инвестирования. В портфельной теории меры риска, связанные с инвестированием в определенный актив или портфель активов, рассчитываются с использованием дисперсии доходности. В математической статистике дисперсия является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания [7, 11].
Если известен полный набор вероятностей исхода события, что достаточно редко встречается на практике, для расчета величины дисперсии используется следующая формула:
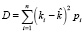
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;
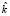– ожидаемая доходность ценной бумаги или актива;
pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования финансовый аналитик обычно располагает статистическими данными о доходности ценной бумаги или актива [1,14]. Если ему доступен весь массив информации, то есть он оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
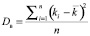
где ki – i-ое значение доходности ценной бумаги;
n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1 [4, 15]. В этом случае формула для ее оценки будет выглядеть следующим образом:
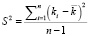
Полученное значение дисперсии характеризует разброс доходности актива или портфеля активов относительно его ожидаемой доходности [9]. Чем больше значение дисперсии, тем выше будет уровень риска. И напротив, низкие значения характеризуют низкий уровень рисков, связанных с осуществлением инвестиций [2, 8].
Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций АО «ПРОМСТРОЙМЕТАЛЛ» и АО «АРМСТИЛЬКАМПАНИ». Предположим, что известен полный набор случайных событий – доходностей с соответствующими им вероятностями, который представлен в таблице.
|
Варианты |
1 |
2 |
3 |
4 |
5 |
|
АО «ПРОМСТРОЙМЕТАЛЛ» |
|||||
|
ki % |
5 |
12 |
23 |
33 |
51 |
|
pi |
0,07 |
0,4 |
0,13 |
0,3 |
0,1 |
|
АО «АРМСТИЛЬКАМПАНИ» |
|||||
|
ki % |
-11 |
-5 |
20 |
35 |
58 |
|
pi |
0,07 |
0,4 |
0,13 |
0,3 |
0,1 |
Изобразим многоугольники распределения, которые дадут приближенное наглядное представление о характере распределения случайной величины. На оси абсцисс отложим доходности активов при i-ом варианте исхода событий, а на оси ординат вероятности i-го варианта исхода событий.
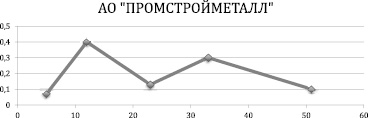
Рис. 1. Многоугольник распределения для АО «ПРОМСТРОЙМЕТАЛЛ»
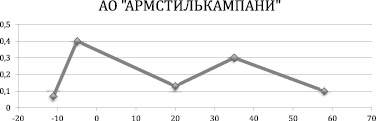
Рис. 2. Многоугольник распределения для АО «АРМСТИЛЬКАМПАНИ»
Ожидаемая доходность для акций АО «ПРОМСТРОЙМЕТАЛЛ» составит 23,14 %, а для акций АО «АРМСТИЛЬКАМПАНИ»16,13 %.
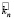= 5*0,07 + 12*0,4 + 23*0,13 +
+ 33*0,3 + 51*0,1 = 23,14 %
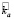= (-11)*0,07-5*0,4 +
+ 20*0,13 + 35*0,3 + 58*0,1 = 16,13 %
В свою очередь, дисперсия доходности акций АО «ПРОМСТРОЙМЕТАЛЛ» будет равна 179,46 %, а акций АО «АРМСТИЛЬКАМПАНИ» 514,19 %
D = (5 – 23,14)2*0,07 + (12 – 23,14)2*0,4 +
+ (23 – 23,14)2*0,13 +
(33 – 23,14)2*0,3 +(51 – 23,14)2*0,1 = 179,46 %
D = ((-11)-16,13)20,07 + ((-5)-16,13)2*0,4 +
+ (20-16,13)2*0,13 + (35-16,13)2*0,3 +
+ (58-16,13)2*0,1 = 514,19 %.
Хотя ожидаемая доходность акций компаний отличается незначительно, риски инвестирования в акции АО «АРМСТИЛЬКАМПАНИ будут существенно выше.
Рассмотрев применение методов математической статистики на примере оценки доходности активов и оценки рисков инвестирования в них, мы убедились в практической значимости математической статистики как науки и необходимости ее изучения для дальнейшего использования в различных сферах деятельности, в том числе и финансовой сфере [3, 13].