1
Попова В.Е.
1
Куршева Т.И.
1
1 ФГБОУ ВО «Ставропольский государственный аграрный университет»
В данной работе мы изучили статистические гипотезы. Мы выяснили, что существует два вида статистических гипотез и различают их по предложению: однозначно определяющая распределение P и утверждающая распределение P. Для определения статистических гипотез используют критические области, которые в свою очередь представляют собой двустороннюю критическую область, левостороннюю критическую область, правостороннюю критическую область. Для изучения статистических гипотез на практике требуется изучать конкретную гипотезу. Так, на практике мы взяли однотипные предприятия региона и проводили анализ по дебиторской задолженности. В ходе работы, мы должны были выявить точечную оценку математического ожидания дебиторской задолженности, определить дисперсию дебиторской задолженности, изучить исправленную выборочную дисперсию, проанализировать статистику критерия и критические значения статистики, а также интервальную оценку дебиторской задолженности однотипных предприятий региона.
статистические гипотезы
математическое ожидание
дисперсия
интервальная оценка
выборочная дисперсия
1. Гулай Т.А., Литвин Д.Б., Долгополова А.Ф. Использование математических методов для анализа динамических свойств управляемого объекта // Моделирование производственных процессов и развитие информационных систем. 2012. С. 167–170.
2. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Математическое моделирование социально-экономических систем // Учетно-аналитические и финансово-экономические проблемы развития региона : Ежегодная 76-я науч.-практ. конф. СтГАУ «Аграрная наука – Северо-Кавказскому региону». 2012. С. 283–286.
3. Гулай Т.А., Долгополова А.Ф., Литвин Д.Б. Личностно-ориентированное обучение математике студентов экономических направлений как средство повышения качества обучения // Теоретические и прикладные проблемы современной педагогики. 2012. С. 28–33.
4. Субоптимальное оценивание вектора угловой скорости объекта по измерениям распределенной акселерометрической системы / Д. Б. Литвин, А. Н. Хабаров, И. П. Шепеть, В. Г. Бондарев, Е. В. Озеров. Вестник АПК Ставрополья. 2013. № 3 (11). С. 60–63.
5. Литвин Д.Б., Гулай Т.А., Долгополова А.Ф. Применение операционного исчисления в моделировании экономических систем // Аграрная наука, творчество, рост. 2013. С. 263–265.
6. Литвин Д.Б., Гулай Т.А., Долгополова А.Ф. Коррекция динамического диапазона статистических данных // Статистика вчера, сегодня, завтра : Междунар. научно-практ. конф., посвященная 155-летию образования Ставропольского губернского комитета статистики, 150-летию образования в России Центрального статистического комитета и Международному году статистики. 2013. С. 148–152.
7. Метод повышения точности измерения векторных величин / Д. В. Бондаренко, С. М. Бражнев, Д. Б. Литвин, А.А. Варнавский. НаукаПарк. 2013. № 6 (16). С. 66–69.
8. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Совершенствование экономических механизмов для решения проблем экологической безопасности // Информационные системы и технологии как фактор развития экономики региона : II Междунар. науч.-практ. конф. 2013. С. 68–71.
9. Литвин Д.Б., Шепеть И.П. Моделирование роста производства с учетом инвестиций и выбытием фондов // Социально-экономические и информационные проблемы устойчивого развития региона: Междунар. науч.-практ. конф. 2015. С. 114–116.
10. Litvin D., Ghazwan R Q. Thinking skills product in mathematics among the students of the university // Экономические, инновационные и информационные проблемы развития региона. : материалы Междунар. науч.-практ. конф. 2014. С. 5–9.
11. Устройство для решения дифференциальных уравнений / И. П. Шепеть, С. М. Бражнев, Д. Б. Литвин, Е.Д. Литвина, А. В. Захарин, С. В. Слесаренок патент на изобретение RUS 2538945 26.12.2013.
12. Литвин Д.Б., Таволжанская О.Н. Элементы математической статистики : учебное пособие. Ставрополь, 2015.
13. Litvin D.B. Mathematical self-concept among university students // Аграрная наука, творчество, рост : сб. науч. тр. по материалам IV Междунар. науч.-практ. конф. 2014. С. 326–329.
14. Применение дифференциального исчисления функций нескольких переменных к разработке алгоритма определения координат объекта / Д. Б. Литвин, И. П. Шепеть, В. Г. Бондарев, Е. Д. Литвина // Финансово-экономические и учетно-аналитические проблемы развития региона : материалы Ежегодной 78-й науч.-практ. конф. 2014. С. 242–246.
14. Литвин Д.Б., Дроздова Е.А. Математическое моделирование в среде визуального программирования. Современные наукоемкие технологии. 2013. № 6. С. 77–78.
Согласно проведенным исследования, статистическая гипотеза – предложение о виде распределения и свойствах случайной величины, которое можно подтвердить или опровергнуть применением статистических методов к данным выборки [2, 9].
Статистические гипотезы различают по виду предложений, содержащихся в них:
- Статистическая гипотеза, однозначно определяющая распределение P, т. е. Hо : {P = P0}, где P0 какой-то конкретный закон, называется простой;
- Статистическая гипотеза, утверждающая принадлежность распределения P к некоторому семейству распределений, то есть вида Hо:{P∈P1}, где P1 – семейство распределений, называется сложной [6, 14].
На практике обычно требуется проверить какую-то конкретную и, как правило, простую гипотезу H0. Такую гипотезу принято называть нулевой [4, 7]. При этом параллельно рассматривается противоречащая ей гипотеза H1, называемая конкурирующей или альтернативной [5, 11].
В большинстве случаев статистические критерии основаны на случайной выборке (X1, X2, … , Xn) фиксированного объема n ≥ 1 для распределения P. В последовательном анализе выборка формируется в ходе самого эксперимента и потому ее размер является случайной величиной [15].
Выделяют три вида критических областей:
- Двусторонняя критическая область определяется двумя интервалами (-∞ ; x α/2) (x1 – α/2; +∞), где xα/2 и x1 – α/2 находят из условий P(φ < xα/2 ) = α/2, P(φ < x1-α/2 ) = 1-α/2;
- Левосторонняя критическая область определяется интервалами (-∞ ; xα), где xα находят из условий P(φ < xα) = α;
- Правосторонняя критическая область определяется интервалом (x1- α ; +∞), где x1- α находят из условия P(φ < x1-α) = 1 – α. [1, 13].
Необходимо проверить с надежностью 0,95 статистическую гипотезу о равенстве средней дебиторской задолженности однотипных предприятий региона значению α₀ = 2 тыс. руб. Для этого была проведена выборочная проверка 15 предприятий региона и их дебиторских задолженностей. Результаты проверки представлены в таблице.
|
i
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
xi (тыс. руб.)
|
1,2
|
0,6
|
1,5
|
0,3
|
0,8
|
1,2
|
2,2
|
1,5
|
2,6
|
5,1
|
0,5
|
1,9
|
1,6
|
8,1
|
3,4
|
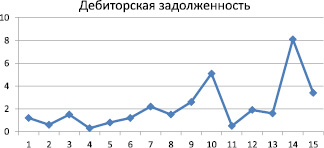
Дебиторская задолженность 15-ти предприятий
Здесь обозначена дебиторская задолженность i-го предприятия через хi.
Найдем точечную оценку математического ожидания дебиторской задолженности, как выборочное среднее [8, 12]:
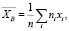
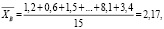 тыс. руб.
тыс. руб.
Найдем выборочную дисперсию дебиторской задолженности:
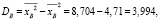 (тыс. руб.)2
(тыс. руб.)2
где 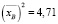 , (тыс. руб.)2;
, (тыс. руб.)2;
 , (тыс. руб.)2 .
, (тыс. руб.)2 .
Найдем исправленную выборочную дисперсию:
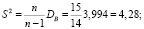
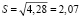 , тыс. руб.
, тыс. руб.
Проверяемая гипотеза H0: 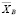 = α₀ = 2 тыс. руб. В качестве альтернативной возьмем гипотезу H1: α0 > 2. Так как генеральная дисперсия σ2 неизвестна, то используем t – критерий Стьюдента [3, 10].
= α₀ = 2 тыс. руб. В качестве альтернативной возьмем гипотезу H1: α0 > 2. Так как генеральная дисперсия σ2 неизвестна, то используем t – критерий Стьюдента [3, 10].
Статистика критерия равна
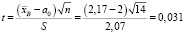 .
.
Критическое значение статистики
 .
.
Так как  , то гипотеза H0 принимается (нет оснований ее отвергнуть). Т.е. на 5 %-ном уровне значимости средняя дебиторская задолженность однотипных предприятий региона равна значению α = 2 тыс. руб.
, то гипотеза H0 принимается (нет оснований ее отвергнуть). Т.е. на 5 %-ном уровне значимости средняя дебиторская задолженность однотипных предприятий региона равна значению α = 2 тыс. руб.
Отыщем интервальную оценку дебиторской задолженности однотипных предприятий региона по имеющимся выборочным данным с надежностью 0,99.
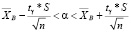
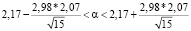
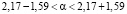
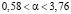
Таким образом, математическое ожидание дебиторской задолженности однотипных предприятий региона с надежностью 0,99 принадлежит интервалу  .
.
Вывод: По имеющимся выборочным данным о проверке дебиторской задолженности предприятий региона отличие выборочного среднего значения задолженности от значения 2000 рублей является статистически не значимым. По этому полагаем среднее значение задолженности принять равным 2 тыс. руб. С надежностью 0,99 математическое ожидание задолженности предприятий региона находятся в интервале 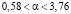 .
.
Библиографическая ссылка
Попова В.Е., Куршева Т.И. ПРОВЕРКА СТАТИСТИЧЕСКОЙ ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНЕЙ ДЕБИТОРСКОЙ ЗАДОЛЖЕННОСТИ ПРЕДПРИЯТИЙ РЕГИОНА // Международный студенческий научный вестник. 2017. № 4-4.
;
URL: https://eduherald.ru/ru/article/view?id=17436 (дата обращения: 06.04.2025).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

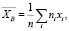
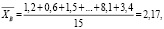 тыс. руб.
тыс. руб.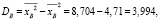 (тыс. руб.)2
(тыс. руб.)2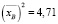 , (тыс. руб.)2;
, (тыс. руб.)2; , (тыс. руб.)2 .
, (тыс. руб.)2 .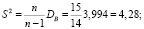
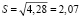 , тыс. руб.
, тыс. руб.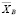 = α₀ = 2 тыс. руб. В качестве альтернативной возьмем гипотезу H1: α0 > 2. Так как генеральная дисперсия σ2 неизвестна, то используем t – критерий Стьюдента [3, 10].
= α₀ = 2 тыс. руб. В качестве альтернативной возьмем гипотезу H1: α0 > 2. Так как генеральная дисперсия σ2 неизвестна, то используем t – критерий Стьюдента [3, 10].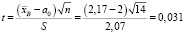 .
. .
. , то гипотеза H0 принимается (нет оснований ее отвергнуть). Т.е. на 5 %-ном уровне значимости средняя дебиторская задолженность однотипных предприятий региона равна значению α = 2 тыс. руб.
, то гипотеза H0 принимается (нет оснований ее отвергнуть). Т.е. на 5 %-ном уровне значимости средняя дебиторская задолженность однотипных предприятий региона равна значению α = 2 тыс. руб.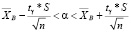
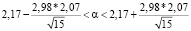
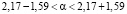
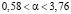
 .
.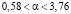 .
.
