Решение полной системы уравнений Навье-Стокса методом сеток
Рассматривается полная система уравнений Навье Стокса, решения которой описывают течения сжимаемого вязкого теплопроводного идеального газа. В системе выполнен переход от переменной плотности и температуры к удельному объему и давлению. Это позволяет решать систему уравнений с частными производными в нормальной форме относительно производных по времени.
В двухмерном случае для безразмерных переменных эта система имеет вид [1]:
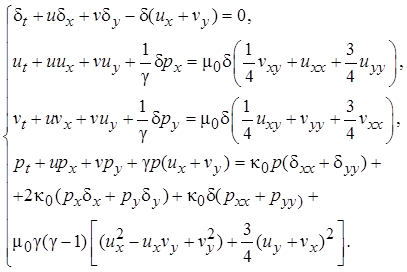 (1)
(1)
Здесь ![]() – время,
– время, ![]() – независимые пространственные переменные. Далее,
– независимые пространственные переменные. Далее, ![]() – удельный объем газа,
– удельный объем газа, ![]() – плотность газа,
– плотность газа, ![]() – давление,
– давление, ![]() – вектор скорости газа с его проекциями на декартовы оси координат
– вектор скорости газа с его проекциями на декартовы оси координат ![]() . Постоянные коэффициенты в уравнениях
. Постоянные коэффициенты в уравнениях ![]() – коэффициенты вязкости и теплопроводности,
– коэффициенты вязкости и теплопроводности, ![]() – показатель политропы идеального газа с уравнениями состояния, записанными в безразмерных переменных
– показатель политропы идеального газа с уравнениями состояния, записанными в безразмерных переменных ![]() Для системы (1) рассматривается начально-краевая задача. В области
Для системы (1) рассматривается начально-краевая задача. В области ![]() задаются начальные условия вида
задаются начальные условия вида
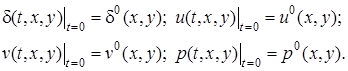 (2)
(2)
А также краевые условия
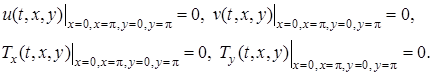 (3)
(3)
Первые из краевых условий (3) обеспечивает прилипание газа на границах области, а вторые – обеспечивает теплоизоляцию на границах. В соответствии с уравнением состояния ![]() , тогда
, тогда ![]() Поэтому для обеспечения теплоизоляции достаточно принять
Поэтому для обеспечения теплоизоляции достаточно принять
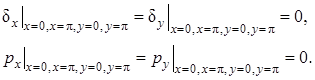
При построении решений с помощью разностных схем по пространственным переменным вводится равномерная сетка ![]() ,
, ![]() . Для дискретизации производных выбираются следующие стандартные выражения (4).
. Для дискретизации производных выбираются следующие стандартные выражения (4).
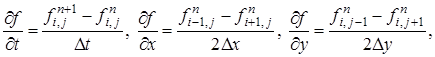
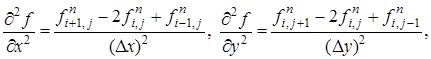 (4)
(4)
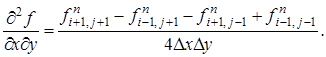
Равенство нулю производной температуры на границах области аппроксимируется уравнениями:
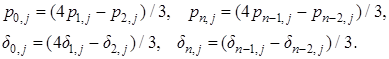
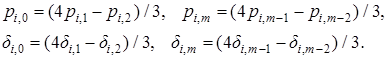 (5)
(5)
Схема решения задачи на GPU c распараллеливанием
Некоторые понятия[2].
· хост (host) = центральный процессор (CPU);
· устройство (device) = графический процессор (GPU);
· поток (stream) - логическая последовательность зависимых асинхронных операций, независимая от операций в других потоках;
· нить (thread) - элементарный параллельный процесс. Все нити группируются в иерархию - grid/block/thread
· грид(grid) - множество процессов, порождаемых запуском ядра
· блок (block) - множество нитей, в рамках блока нити могут быть синхронизованы, и могут иметь общую разделяемую (shedder) память.
Нити в блоках и блоки в гриде могут быть представлены в виде одно-, двух- или трёхмерной решетки, мы будем рассматривать одномерный грид и блок.
· варп (warp) - группа нитей, размер варпа 32 нити. Все нити одного варпа выполняются одновременно и синхронно (SIMD) на своём мультипроцессоре.
· ядро (kernel) - функция, параллельно выполняемая потоками на GPU;
Программа состоит из двух частей:
· host-кода (управляющего кода) написанного на обычном С/С++, выполняется на CPU
· device-кода (аппаратного кода) на GPU исполняются специальные функции – ядра(kernel) и функции, вызываемые внутри них.
Ядро является потоковой (stream) функцией – большое количество нитей (threads) параллельно исполняют тело ядра(kernel). Ядро вызывается со стороны CPU, при этом указывается количество блоков и количество нитей в каждом блоке, которые будут его исполнять, а так же номер потока в котором будет выполняться ядро. Если номер потока не указан, то ядро будет выполнено в нулевом потоке. Нулевой поток всегда синхронен.
Потоки бывают синхронные и асинхронные. Синхронный поток означает, что после вызова ядра, CPU будет ждать, когда GPU завершит работу и после продолжит алгоритм. Если поток асинхронен, то CPU после вызова ядра, продолжит выполнять алгоритм, не дожидаясь завершения работы GPU.
Имеем слой ![]() элементов с шагом
элементов с шагом ![]() и
и ![]() соответственно[3,4]. На основании пяти элементов данного слоя с шагом по времени
соответственно[3,4]. На основании пяти элементов данного слоя с шагом по времени ![]() вычисляются элементы следующего слоя. На CPU задача решается введением двойного цикла. Идея решения задачи с распараллеливанием заключена в том, чтобы все элементы слоя были вычислены одновременно, то есть на GPU в рамках первого этапа запускается один поток с количеством нитей равном
вычисляются элементы следующего слоя. На CPU задача решается введением двойного цикла. Идея решения задачи с распараллеливанием заключена в том, чтобы все элементы слоя были вычислены одновременно, то есть на GPU в рамках первого этапа запускается один поток с количеством нитей равном ![]() , которые параллельно вычисляют элементы следующего слоя с шагом
, которые параллельно вычисляют элементы следующего слоя с шагом ![]() . Процесс продемонстрирован на рисунке 1. По цветам, черные – вычисленные, белые – необходимо вычислить, желтые – вычисляются.
. Процесс продемонстрирован на рисунке 1. По цветам, черные – вычисленные, белые – необходимо вычислить, желтые – вычисляются.
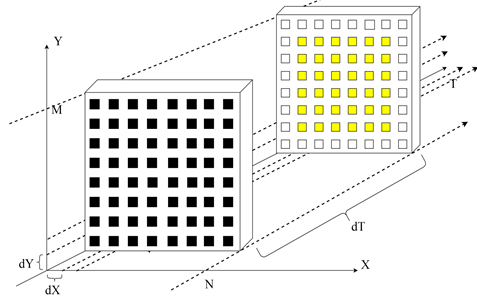
Рис.1 Первый этап - нахождение элементов в следующем слое на GPU.
2 этап заключается в вычислении граничных элементов. Граничные элементы вычисляются в два асинхронных потока (зеленым выделен первый поток, красным второй поток), первый имеет ![]() нитей и каждая нить вычисляет два элемента, второй поток имеет
нитей и каждая нить вычисляет два элемента, второй поток имеет ![]() нитей и каждая нить также вычисляет два элемента. Для наглядности процесс показан на рисунке 2.
нитей и каждая нить также вычисляет два элемента. Для наглядности процесс показан на рисунке 2.
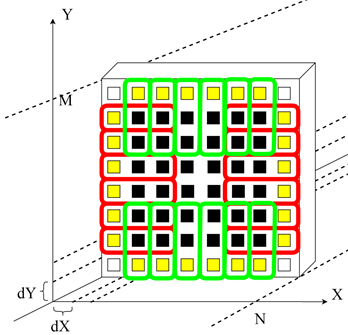
Рис.2 Второй этап – нахождение краевых элементов на GPU.
Угловые элементы вычисляются в конце второго этапа нитью с глобальным индексом “0”.
Приведем листинг вызова ядер (рис. 3)[5,6], для нахождения элементов слоя. Как видно из листинга первый вызов ядра проходит в нулевом потоке, нулевой поток синхронен, как если бы cudaDeviceSynchronize() (функция синхронизации) вставлен до и после каждой CUDA операции. Второй и третий вызов ядра происходит в асинхронных потоках, то есть они выполняются одновременно.
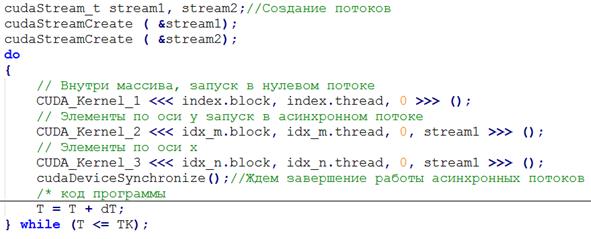
Рис. 3 – Листинг организации вызова ядер.
Эффективность использования CPU и CPU+GPU
В Табл. 1 приведено программно-аппаратное обеспечение, на котором производились расчеты. В Табл. 2 полученные результаты расчетов.
Программно-аппаратная часть. Таблица 1
|
Аппаратное обеспечение |
|
|
Видео адаптер |
Nvidia Geforce GTX 650, 1024 Мб DDR5 |
|
Центральный процессор |
Intel Pentium G3260 3,3 ГГц |
|
Оперативная память |
2 ГБ 2хDDR3-1333 ГГц |
|
Программное обеспечение |
|
|
Операционная система |
Windows 7 64 bit |
|
Драйвер |
NVIDIA Driver for Windows 381.65 |
|
Среда программирования |
Microsoft Visual Studio 2015 Enterprise |
|
Версия CUDA Toolkit |
CUDA Toolkit 8.0.61 for Windows |
Сравнение скорости вычислений Таблица 2
|
N,M |
GPU+CPU, мс |
CPU, мс |
Во сколько раз быстрей |
|
256 |
0,6 |
19,9 |
33,13 |
|
512 |
2,1 |
117,6 |
56,00 |
|
768 |
5,1 |
397,6 |
77,96 |
|
1024 |
8,5 |
746,48 |
87,82 |
|
1280 |
14,1 |
1204,0 |
85,39 |
|
1536 |
20,4 |
1810,5 |
88,75 |
|
1792 |
27,8 |
2584,4 |
92,96 |
|
2048 |
34,1 |
3432,8 |
100,67 |
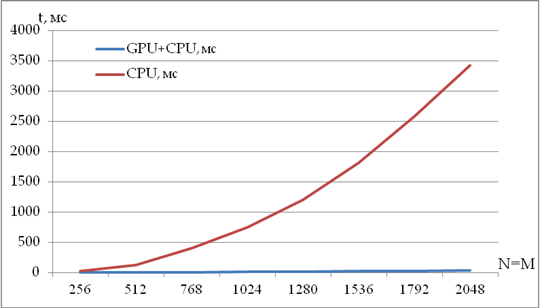
Рис.4 График затраченного времени на вычисление одного слоя.
Как видно из результатов (рис 4), при параллельной работе графического адаптера ускорение обработки данных увеличивается в десятки раз. Отношение времени обработки данных на графическом адаптере и центральном процессоре не постоянно, а зависит от размера задачи. Чем больше объем задачи, тем выгоднее использовать графический процессор.
Результаты моделирования
В соответствии с системой (1), начальными (2) и граничными (3) условиями записываются разностные уравнения. Для конкретного расчета выберем значения переменных для момента времени t=0, ![]() и значения констант
и значения констант ![]() и шага по времени
и шага по времени ![]() .
.
Расчет произведен при следующих параметрах. Размер сетки - ![]() шаг моделирования -
шаг моделирования - ![]() Коэффициенты вязкости и теплопроводности.
Коэффициенты вязкости и теплопроводности. ![]() ,
, ![]() Для контроля адекватности модели и точности вычислений был проведены расчеты на больших промежутках времени до достижения состояния однородного покоя. При
Для контроля адекватности модели и точности вычислений был проведены расчеты на больших промежутках времени до достижения состояния однородного покоя. При ![]() этот промежуток приближенно равен
этот промежуток приближенно равен ![]() .
.
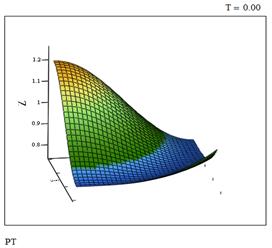
Рис. 5 Давление в момент времени t=0
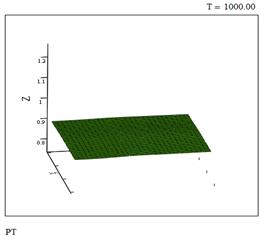
Рис. 6 – Давление в момент времени t=1000
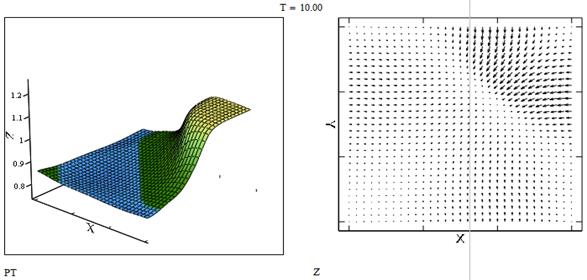
Рис. 7 Давление и распределение скоростей в момент времени t=10
Разница колебаний между минимумом и максимумом давления на покое составляет менее 0,016 (рисунок 6).
Затраченное машинное время на моделирование с использованием GPU 15 часов 30 минут. Всего было найдено 100 млн слоев, такая задача на CPU решалась бы около 3-х недель.
Видео моделирования доступно по ссылке: https://cloud.mail.ru/public/LTLz/BQyLMM3Jf
Библиографическая ссылка
Маркин Е.Е., Скачков П.П. ГЕТЕРОГЕННЫЕ ПАРАЛЛЕЛЬНЫЕ ВЫЧИСЛЕНИЯ НА ПРИМЕРЕ РЕШЕНИЯ ПОЛНОЙ СИСТЕМЫ УРАВНЕНИЙ НАВЬЕ-СТОКСА МЕТОДОМ СЕТОК // Международный студенческий научный вестник. 2017. № 5. ;URL: https://eduherald.ru/ru/article/view?id=17349 (дата обращения: 06.04.2025).

