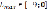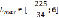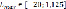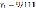Каждый студент задаётся вопросом: ″Для чего нужно линейное программирование?″ Рассмотрим значимость линейного программирования с точки зрения производства и предпринимательства.
Используя методы графического решения линейного программирования, производитель может найти оптимальный производственный план, при котором будет достигаться максимум прибыли при минимуме издержек, а также проследить за тем, как будет изменяться прибыль при изменении величины ресурсов. Приведём следующий пример.
Дана функция: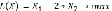 
, с ограничениями:
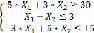
Проанализируем функцию на устойчивость. График нашей функции будет выглядеть следующим образом:
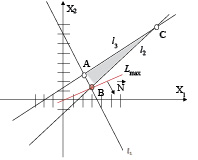
Интересующая нас область является фигурой ABC.
После изменения коэффициентов целевой функции и анализа изменений констант в правой части неравенств ограничений мы получим стоимость ресурсов, которая выглядит следующим образом:
|
Стоимость ресурсов |
||
|
Дефицитные ресурсы |
Недефицитные ресурсы |
|
|
|
|
|
|
Интервал устойчивости |
||
|
[0;111] |
[-30/17;6] |
[-5,25;50] |
|
Оптимальное значение целевой функции |
||
|
|
|
|
|
Мера устойчивости (условная стоимость) |
||
|
|
|
|
В итоге, мы получаем максимальное значение Lmax =1,125, достигающееся при величинах Х1 = 39/8 и Х2 = 15/8. Интервалы устойчивости активных запасов:
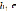[0;111]; 
,
; 
.
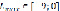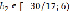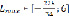Для пассивных запасов:
.
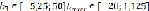Стоимость ресурсов:
; 
; 
.
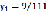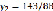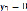С учётом проведения анализа устойчивости, производитель будет производить продукцию на основании полученного плана, что, несомненно, будет положительно сказываться на его ведении дел.
Библиографическая ссылка
Карнавская Н.В., Яшина Ю.Е., Чехута В.А., Зотова С.А., Матвеева Т.А. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. ГРАФИЧЕСКОЕ РЕШЕНИЕ И АНАЛИЗ УСТОЙЧИВОСТИ НАЙДЕННОГО ОПТИМУМА // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14167 (дата обращения: 21.11.2024).