В настоящее время ведутся исследования во многих перспективных научно-технических направлениях, которые относятся к функциональной микроэлектронике [1-3]. Наиболее известными среди них являются акустоэлектроника, которая использует распространение акустических волн в твердом теле, пьезоэлектрический, магнитострикционный эффекты и акустико-оптические явления. Малая скорость распространения акустических волн и малая длина их волны позволяют реализовать миниатюрные линии задержки, фильтры с заданными свойствами, усилители СВЧ [4-5].
В данной работе мы предлагаем теоретическое исследование спектра собственных частот упругих колебаний в тонких пластинах и пленках железо-иттриевого граната (ЖИГ).
Теоретическое исследование спектра собственных частот упругих колебаний будем выполнять в рамках феноменологического подхода на основе решения линеаризованного уравнения движения вектора упругого смещения при учете граничных условий на поверхностях пластины или пленки ЖИГ.
Рассмотрим тонкую пластину и пленку ЖИГ толщиною S (рис. 1)
Рисунок 1. Тонкая пластина или пленка ЖИГ
Будем полагать, что ось z направлена перпендикулярно к поверхности пластины или пленки ЖИГ и совпадает с кристаллографической осью кубического кристалла [111], так как упругие свойства ЖИГ считаются анизотропными.
В данном случае задача по определению спектра собственных частот упругих колебаний сводится к следующему уравнению
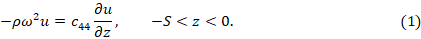
Здесь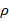 
– плотность ЖИГ, 
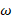– угловая частота, 
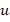– упругое смещение в ЖИГ, 
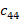– компонента тензора упругости (упругая постоянная ЖИГ).
Введем следующее обозначение:
Теперь уравнение (1) можно записать в виде:
Корни характеристического уравнения дифференциального уравнения (3) можно записать в виде:
Выражение (4) показывает, что в тонкой пластине или пленке ЖИГ могут существовать две моды. Они соответствуют двум поперечным упругим волнам, каждая из которых может распространяться в положительном и отрицательном направлениях оси z.
Учтя выражение (4), решение уравнения (3) теперь можно представить в виде:
Рассмотрим следующие граничные условия:
Подставим выражение (5) в граничные условия (6)-(7) получим следующую систему линейных алгебраических уравнений:
Приравняем определитель из выражений при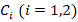 
после ряда преобразований получим уравнение, которое определяет возможные значения волнового вектора 
:
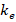Отсюда
и спектр собственных частот упругих колебаний в тонких пластинах и пленках ЖИГ:
Из выражения (12) видно, что собственные частоты упругих колебаний в тонких пластинах и пленках ЖИГ зависят от упругих свойств, плотности и толщины пластины и пленки. Следует отметить, что по формуле (12) можно определить спектр собственных частот упругих колебаний можно определить в тонких упругих пластинах любой толщины и изготовленных из любых материалов.