Актуальность выбранной темы исследования заключается в том, что в связи с введением ФГОС НОО, обучающимся необходимо развивать универсальные учебные действия, которые направлены на достижение личностных, метапредметных и предметных результатов. Личностные, регулятивные, коммуникативные и познавательные универсальные учебные действия являются основными видами универсальных учебных действий начального общего образования. В соответствии со стандартами второго поколения, познавательные универсальные учебные действия включают в себя общеучебные и логические действия.
Мы рассмотрим логические универсальные действия, которые включают в себя следующее:
- анализ объектов с целью выделения признаков (существенных, несущественных);
- синтез - составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов;
- выбор оснований и критериев для сравнения, сериации, классификации объектов;
- подведение под понятие, выведение следствия; установление причинно-следственных связей;
- построение логической цепи рассуждении;
- доказательство, выдвижение гипотез и их обоснование.
Согласно определению В. В. Давыдова, «логическое мышление – это способность и умение ребенка младшего школьного возраста, самостоятельно производить логические действия: анализ, синтез, сравнение, обобщение, решение составных словесно-логических задач, индуктивные и дедуктивные логические схемы» [2]. Мыслительные операции, представленные в данном определении, отражают необходимость развития у младших школьников способности к решению словесно-логических задач. В современных образовательных учреждениях от обучающихся требуется не просто решать текстовые задачи, задачи на сравнение и задачи с выбором арифметических действий, а требуется также производить логические действия, учиться мыслить нестандартно, находить причинно-следственные связи. Всё вышеперечисленное, по нашему мнению, можно достичь с помощью решения логических задач. От текстовых задач логические задачи отличаются тем, что они не требуют арифметических вычислений, а решаются с опорой на определение и анализ отношений между всеми объектами задачи.
Из нашего опыта и опроса учителей г. Красноярска, мы можем говорить о том, что на уроках математики недостаточно времени уделяется решению логических задач.
Нами был проведен сравнительный анализ учебников по математике для 3-го класса. Первое учебное пособие относится к развивающей системе обучения Занкова Л. В. – авторы учебника Аргинская И. И., Иванова Е. И., Кормишина С. Н. [1]. Второе учебное пособие относится к традиционной системе обучения, а именно программе «Школа России» - авторы учебника Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. [3].
Сравнив материалы данных учебных пособий, и календарно-тематическое планирование мы установили, что в развивающей системе Занкова Л. В. для решения задач уделяется 18 часов в течение года, из них 1 час – на решение словесно-логических задач с помощью таблицы. В традиционной системе обучения программы «Школа России» на решение задач уделяется 28 часов, на решения словесно-логических задач как отдельного вида задачи, количество времени не уточняется.
Кроме того, на основе проведенного нами анализа вышеуказанных учебных пособий, мы установили, что в учебнике Аргинской И. И. основным видом логической задачи является словесно-логическая, которая требует от младшего школьника способности к нестандартному мышлению, умению находить различные пути решения задач, использовать доказательные рассуждения. В учебном пособии Моро М. И. представлены разные виды логических задач и упражнений, а именно: задачи на развитие умения определять геометрические фигуры и узнавать их по описанию, задачи на выявление существенных признаков предмета и исключения лишнего, решение математических ребусов, судоку и цепочек последовательностей.
Нами был разобран пример решения задач вышеуказанных учебных пособий. Из первого пособия развивающей системы Занкова Л.В., нами представлена словесно-логическая задача, а из учебного пособия традиционной системы обучения программы «Школа России» представлено задание «магический квадрат».
Пример 1. В кувшин, бутылку и стакан налили сок, молоко и компот. Известно, что молоко находится не в стакане, а сок налит не в бутылку и не в стакан. Какой напиток, в каком стакане находится? [1. C.72].
Решение.
Составим таблицу, где учитывались бы все возможные варианты, предложенные для рассуждения. Нам известно из первого условия, что молоко находится не в стакане, а из второго, что сок налит не в бутылку и не в стакан. Значит, можно ставить знак «-» в соответствующих клетках [5].
Таблица 1
|
|
Сок |
Молоко |
Компот |
|
Кувшин |
+ |
- |
- |
|
Бутылка |
- |
+ |
- |
|
Стакан |
- |
- |
+ |
Начнем рассуждение с того, что определим, что сок у нас налит в кувшине, так как не налит в бутылку и стакан по условию, ставим знак «+» в соответствующей клетке. Далее рассуждаем так: молоко не налито в стакан по условию, а кувшин занят соком, делаем вывод о том, что молоко налито в бутылку, ставим знак «+». Остается стакан, в котором налит компот, так как свободных емкостей не осталось, ставим знак «+». Записываем ответ задачи: сок налит в кувшине, молоко в бутылке, а компот в стакане.
Пример 2. Проверь, магические ли это квадраты. [3.C29].
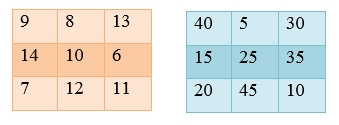
Рис. 1. Магические квадраты
Для решения такого задания, необходимо установить то, чем является магический квадрат и как его решать. Магический квадрат - это квадрат, в котором если складывать три числа по вертикали, горизонтали, диагонали, то значение должно быть равным.
Рассмотрим первый квадрат, первую строку:
9+8+13=30
Аналогично рассуждая, проверим остальные строки и столбцы:
14+10+6=30
7+12+11=30
9+14+7=30
8+10+12=30
13+6+11=30
9+10+11=30
После проведенных действий делаем вывод о том, что во всех выражениях значение равно 30, значит, квадрат является магическим.
Затем рассмотрим второй магический квадрат и проводим с ним аналогичные действия. Определяем, являются ли квадраты магическими. Данное задание на смекалку предусматривает развитие логического мышления, но этого недостаточно для его качественного развития потому, что проводится работа с операцией сложения, которая не подразумевает выполнение действий с использованием сложных мыслительных операций, как например, при решение словесно-логической задачи.
Проанализировав вышеуказанные пособия, нами было установлено, что в развивающей системе обучения Занкова Л. В. – 9 логических задач, а в традиционной системе программы «Школа России» – 8 логических задач. Также в учебном пособии автора Моро М. И. представлены логические задачи, которые не являются обязательными для решения обучающимися на уроках математики, так как выступают в качестве дополнительного материала к занятиям, это приводит к недостаточному развитию логического мышления обучающихся. Мы рекомендуем учителям начальных классов включать решения логических задач в образовательный процесс, наравне с решением текстовых задач, для которых необходим выбор арифметических действий, в связи с тем, что это будет способствовать полноценному развитию логического мышления младших школьников.
Проведя сравнительный анализ вышеуказанных пособий, нами были сделаны следующие выводы:
- Задачи на развитие логического мышления в учебниках математики присутствуют, но в недостаточном количестве, по сравнению с текстовыми задачами, для которых обязателен выбор арифметического действия.
- Логические задачи однотипны и неразнообразны. На уроках математики в 3 классе стандартно используются словесно-логические задачи, другие виды логических задач необязательны к решению обучающимися, и задачи не входят в календарно-тематическое планирование.
- Для продуктивного и полноценного развития логического мышления у младших школьников, необходимо комплексно включать в программу обучения математики логические задачи.

