В машиностроении расчету на прочность и жесткость пластин предшествует определение напряженно-деформированного состояния при соответсвующих граничных условиях. Расчету предшествует математическая модель, основанная на гипотезах и методах теории упругости.
Постановка задачи с точки зрения теории упругости. Рассматривается упругое равновесие однородной анизотропной пластинки под действием внешних поверхностных усилий 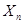 ,
, 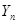 и
и 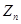 . Материал пластинки слабо анизотропен и ортотропен. Через все точки тела проходят три взаимоперпендикулярные плоскости упругой симметрии, относительно которых наблюдается симметрия в упругих свойствах (плоскости ортотропии). Геометрические оси совпадают с осями анизотропии.
. Материал пластинки слабо анизотропен и ортотропен. Через все точки тела проходят три взаимоперпендикулярные плоскости упругой симметрии, относительно которых наблюдается симметрия в упругих свойствах (плоскости ортотропии). Геометрические оси совпадают с осями анизотропии.
Обобщенный закон Гука для ортотропной среды в случае обобщенного плоского напряженного состояния имеет вид [6]:
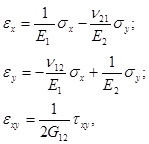 (1)
(1)
где 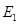 и
и 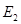 модули упругости в направлении оси x и y соответственно,
модули упругости в направлении оси x и y соответственно, 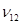 и
и 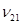 – коэффициенты Пуассона (
– коэффициенты Пуассона (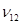 – коэффициент, характеризующий сокращение в направлении х при растяжении в направлении y,
– коэффициент, характеризующий сокращение в направлении х при растяжении в направлении y, 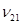 – коэффициент, характеризующий сокращение в направлении y при растяжении в направлении x), причем
– коэффициент, характеризующий сокращение в направлении y при растяжении в направлении x), причем 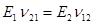 ,
, 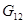 – модуль сдвига в плоскости xy.
– модуль сдвига в плоскости xy.
Для решения задачи применяется метод малого параметра [9], основанный на представлении искомых функции в виде ряда, расположенного по степеням некоторых малых параметров, что позволяет свести задачу для анизотропной среды к плоской задачи для изотропной среды.
Закон Гука для случая изотропной среды может быть представлен в виде [7]:
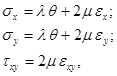 (2)
(2)
где 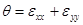 – объемная деформация,
– объемная деформация, 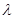 и
и 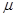 – параметры Ламе, причем
– параметры Ламе, причем 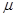 – модуль сдвига в изотропной среде.
– модуль сдвига в изотропной среде.
Придадим соотношениям (1) для ортотропной среды вид зависимостей (2) для изотропной среды. После преобразований получим:
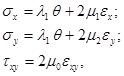 (3)
(3)
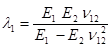 ;
; 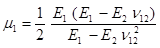 ;
; 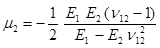 ;
; 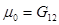 ,
,
где 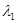 ,
, 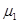 ,
, 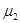 и
и 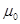 – параметры, зависящие от упругих свойств материала.
– параметры, зависящие от упругих свойств материала.
Для построения решения необходимо определить параметры изотропной среды основываясь на известных параметрах ортотропной среды.
Модуль упругости 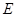 примем как среднее значение:
примем как среднее значение: 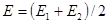 .
.
Коэффициент Пуассона 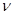 примем равным таковому в анизотропной среде
примем равным таковому в анизотропной среде 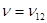 .
.
Модуль сдвига 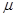 определится зависимостью [6]
определится зависимостью [6] 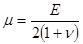 .
.
Параметр Ламе 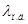 вычисляем сначала для случая плоской деформации [7]
вычисляем сначала для случая плоской деформации [7] 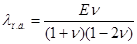 , затем для случая обобщенного плоского напряженного состояния [6]
, затем для случая обобщенного плоского напряженного состояния [6] 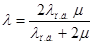 .
.
Введем малые параметры 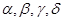 :
:
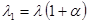 ;
; 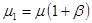 ;
; 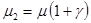 ;
; 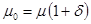 . (4)
. (4)
Можно убедиться, что при любых значениях технических постоянных, параметры 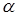 и
и 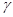 равны, поэтому примем
равны, поэтому примем 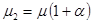 и варьировать будем три параметра.
и варьировать будем три параметра.
Окончательно закон Гука (3) для слабо анизотропной среды можно рассматривать с учетом (4) как «возмущение» изотропной среды.
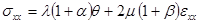 ;
;
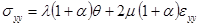 ; (5)
; (5)
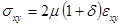 .
.
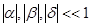 ;
; 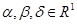 .
.
При 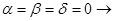 линейная изотропия.
линейная изотропия.
Для кратности здесь и далее обозначим:
1) 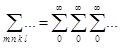 ;
;
2) в записи 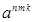 верхний составной индекс идентифицирует элемент в асимптотическом разложении
верхний составной индекс идентифицирует элемент в асимптотическом разложении
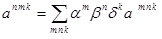 ,
,
а не степень.
Асимптотические ряды:
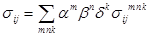 ;
;
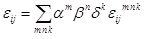 ; (6)
; (6)
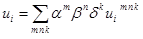 ;
;
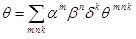 .
.
Такое представление унифицирует все индексы в 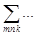 , поэтому все слагаемые можно определить внутри единой суммы и, далее, каждую скобку внутри
, поэтому все слагаемые можно определить внутри единой суммы и, далее, каждую скобку внутри 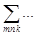 приравнять нулю (декомпозиция).
приравнять нулю (декомпозиция).
Декомпозиция определяющих соотношений:
1. Закон Гука:
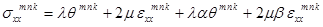 ;
;
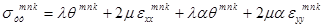 ; (7)
; (7)
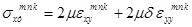 .
.
2. Соотношения Коши:
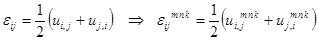 . (8)
. (8)
3. Уравнения равновесия:
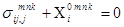 , (9)
, (9)
где 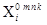 – массовые силы.
– массовые силы.
Нахождение частного решения от произвольно заданных массовых сил представляет некоторую трудность, однако в случае многочленов принципиальных трудностей нет.
Система уравнений (7), (8) и (9) по форме отвечает всем соотношения изотропной теории упругости. На каждом шаге 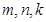 решается традиционная задача теории упругости для изотропного тела, причем всегда при одном и том же наборе параметров упругости
решается традиционная задача теории упругости для изотропного тела, причем всегда при одном и том же наборе параметров упругости 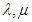 .
.
Таким образом, для решения слабо анизотропной задачи во втором приближении необходимо решить 8 задач о распределении напряжений в изотропной пластинке той же формы.
Заданные граничные условия (включая массовые силы) сразу учитываются в нулевом приближении; затем поправки в граничных условиях от 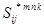 вычитаются из «нулевых» граничных условий. Необходимо вносить поправки в механические поля и от «фиктивных» массовых сил
вычитаются из «нулевых» граничных условий. Необходимо вносить поправки в механические поля и от «фиктивных» массовых сил 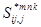 . Например, граничные условия на позиции
. Например, граничные условия на позиции 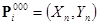 , а на позиции
, а на позиции 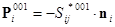 .
.
Полученные поля напряжений 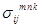 , деформаций
, деформаций 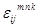 и перемещений
и перемещений 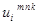 суммируются согласно (7).
суммируются согласно (7).
В работе [4] рассматривалось равновесие круговой пластинки под действием усилий распределенных по боковой поверхности вызывающие однородное напряженное состояние. В работе [5] исследовалось равновесие призматического тела под действием усилий распределенных по торцам.
Решение задачи. Рассматривается прямоугольная пластинка (рис. 1) из поликристаллического алюминия [1] 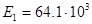 МПа;
МПа; 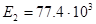 МПа;
МПа; 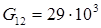 МПа;
МПа; 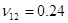 .
.
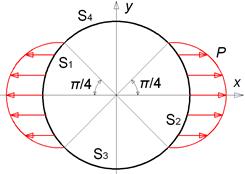
Рис. 1. Ортотропная плпстинка
Граничные условия:
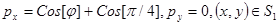 ;
;
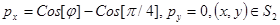 ;
;
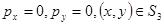 ;
;
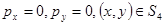 .
.
Массовые силы отсутствуют, 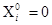 . Геометрическая и физическая стороны задачи рассматриваются в обезразмеренном виде с размерным коэффициентом
. Геометрическая и физическая стороны задачи рассматриваются в обезразмеренном виде с размерным коэффициентом 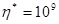 Па.
Па.
Решение задачи в целом, проводится с помощью метода малого параметра по методике, описанной выше, а изотропная задача теории упругости для пластинки на каждом приближении решается методом граничных состояний (МГС) [8].
Параметры изотропной среды:
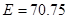 ,
, 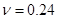 ,
, 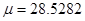 ,
, 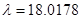 .
.
Согласно (3), (4) и (5) малые параметры:
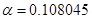 ,
, 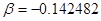 ,
, 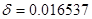 .
.
Полученные в результате решения во втором приближении компоненты вектора перемещения слишком громоздки для полной обозримости, поэтому представим лишь их структуру (высшие степени и произведения малых параметров, начиная с 3-го порядка, отброшены):
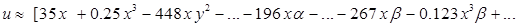
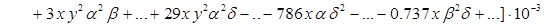 ;
;
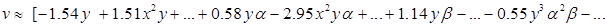
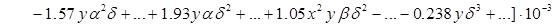 .
.
Для получения окончательных выражений, содержащих технические константы необходимо из (5) выразить малые параметры, подставить их в полученные выражения и провести обратную параметризацию.
Таким образом, мы получили механические характеристики как функции координат и малых параметров. Изменяя последние в определенных пределах, мы имеем возможность получать механические поля, не проводя каждый раз заново решение анизотропной задачи, что порой при сложных граничных условиях и геометрии тела, составляет непростую задачу, особенно если они имеют технологические отверстия [2], [3].

