Современные материалы, применяемые в авиастроении, строительстве, машиностроении с точки зрения теории упругости характеризуются как анизотропные, то есть материалы, у которых наблюдается различие в упругих свойствах для разных направлений. Если различия в упругих свойствах материала невелики, то такие среды называются слабо анизотропными, т.е. мало отличающихся от изотропных. Такая форма анизотропии наводится, например, в результате механической обработки, термообработки и других технологических процессов. С точки зрения математического моделирования, основным методом решения задач теории упругости для тел из таких материалов, является метод малого параметра (метод Пуанкаре). Немаловажную часть этого метода составляет способ введения малых параметров и их количество.
В настоящей работе предлагается приближенный способ решения пространственной статической задачи теории упругости для транверсально-изотропного тела со слабо выраженной анизотропией.
1. Обзор известных работ. Данной проблеме посвятил ряд работ С.Г. Лехницкий [6]. Он рассматривал плоскую ортотропную задачу и предложил метод разложения функции напряжений в ряд по двум параметрам, за которые он принимал малые отклонения от комплексных параметров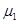 
и 
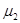равных 
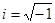для изотропной среды.
, 
,
, 
,
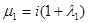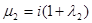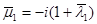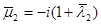где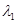 
и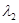 
– параметры, малые по сравнению с единицей настолько, что пренебрегаются высшие степени и произведения этих величин, начиная от 3-го порядка. Функция напряжений, через которую определяются напряжения, деформации и перемещения имеет вид:
,
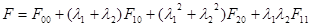где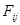 
– функции координат x и y.
В работе А.В. Саченкова и В.И. Дарагана [8] рассматривались два способа представления уравнения совместности деформаций для ортотропного материала при совщении осей с главными направлениями упругости.
В первом из них уравнение совместности имело вид:
,
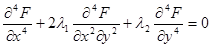где
, 
.
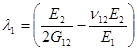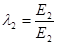Здесь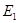 
, 
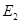– модули упругости по главным направлениям x и y; 
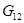– модуль сдвига; 
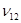– коэффициент Пуассона (обозначение технических констант в [8] отличается от выше приведенного).
Далее вводится новая переменная:
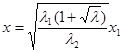, где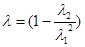 
.
Уравнение (1.1) принимает вид:
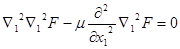, (1.1)
где
, 
.
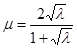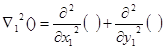И решение уравнения (1.1) ищется в виде:
.
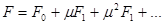Во втором способе, уравнение (1.1) преобразуется с помощью переменных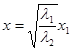 
, 
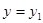и приводится к уравнению:
,
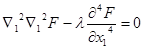решение которого:
.
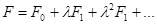Причем следует отметить, что в первом, что и во втором способах, чем меньше параметры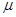 
и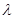 
, тем сходимость наблюдается быстрее.
2. Постановка задачи и теоретическое обоснование. Рассматривается упругое равновесие однородного анизотропной тела под действием внешних поверхностных усили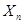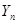й 
, 
и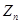 
. Материал тела слабо анизотропен и трансверсально-изотропен. Через все точки тела проходят параллельные плоскости упругой симметрии, в которых все направления являются упруго-эквивалентными (плоскости изотропии).
Для решения задачи применяется метод малого параметра [9], основанный на представлении искомых функции в виде ряда, расположенного по степеням некоторых малых параметров, что позволяет свести решение задачи для анизотропной среды к решению ряда плоских задач для изотропной среды.
Придадим обобщенному закону Гука для транстропной среды [6] следующий вид:
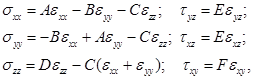(2.1)
где А, B, С, D, E, F – константы, зависящие от упругих свойств трансверсально-изотропного материала.
; 
; 
; 
; 
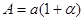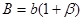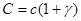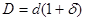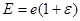; (2.2)
,
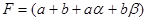где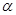 
, 
, 
, 
, 
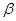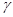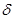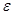– малые параметры, характеризующие отклонение слабо анизотропной среды от некоторой изотропной среды.
Таким образом, вариации подлежат пять малых параметров 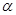, , 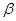, , 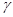, 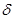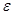которые соответствуют пяти независимым константам упругости для транстропной среды.
Окончательно закон Гука (2.1) для слабо анизотропной среды можно рассматривать с учетом (2.2) как «возмущение» изотропной среды.
; 
;
; 
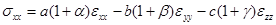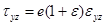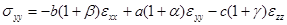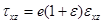; (2.3)
; 
.
; 
.
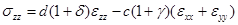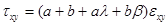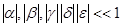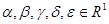При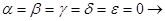 
линейная изотропия.
Для кратности здесь и далее обозначим:
1) 
;
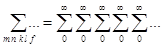2) в записи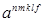 
верхний составной индекс идентифицирует элемент в асимптотическом разложении
,
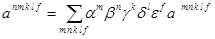а не степень.
Асимптотические ряды:
;
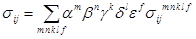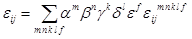; (2.4)
.
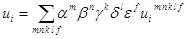Такое представление унифицирует все индексы в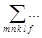 
, поэтому все слагаемые можно определить внутри единой суммы и, далее, каждую скобку внутри 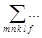приравнять нулю (декомпозиция).
Декомпозиция определяющих соотношений:
1. Закон Гука:
;
;
;
;
;
.
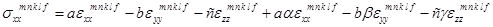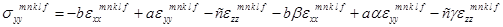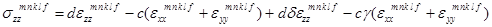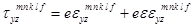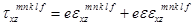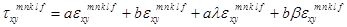2. Соотношения Коши:
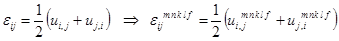. (2.5)
3. Уравнения равновесия:
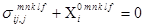, (2.6)
где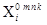 
– массовые силы.
Необходимо организовать перебор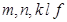 
так, чтобы кроме полей характеристик на определенной позиции, в уравнениях участвовали поля, ранее уже полученные.
Нахождение частного решения от произвольно заданных массовых сил представляет некоторую трудность, однако в случае многочленов принципиальных трудностей нет.
На каждом шаге 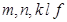решается традиционная задача теории упругости для изотропного тела, причем всегда при одном и том же наборе параметров упругости 
.
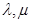В работах [2] и [3], рассмотрены задачи для призматического в плане тела с неоднородными нагрузками, приложенными к торцам тела. В работе [5] реализована методика построения параметрического решения для круговой пластинки; выписано явное решение для конкретной краевой задачи.
3. Решение задачи. Рассматривается первая основная задача для стержня прямоугольной формы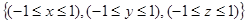 
из меди [1] 
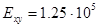МПа; 
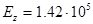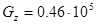МПа, 
МПа;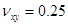 
, 
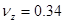. На боковой поверхности заданы усилия:
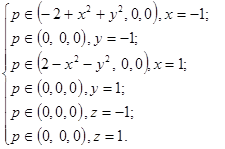
Постоянные, характеризующие изотропную среду: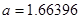 
, 
, 
, 
, 
.
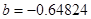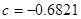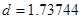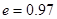Малые параметры, «отклоняющие» слабо анизотропную среду от изотропной: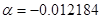 
, 
, 
, 
, 
.
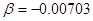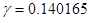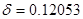Массовые силы отсутствуют,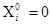 
. Геометрическая и физическая стороны задачи рассматриваются в обезразмеренном виде с размерным коэффициентом 
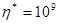Па.
Решение задачи в целом, проводится методом малого параметра по методике, описанной выше, а изотропная задача теории упругости на каждом приближении решается методом граничных состояний (МГС) [7].
Полученные результаты решения во втором приближении слишком громостки, поэтому приведем лишь структуру компонент вектора перемещения (высшие степени и произведения малых параметров отброшены):
;
;
.
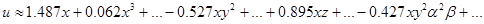
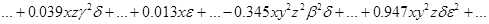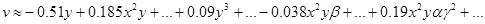
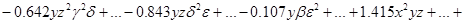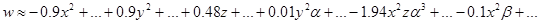
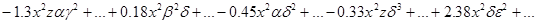Таким образом, механические характеристики есть функции координат и малых параметров. Изменяя последние в определенных пределах, мы имеем возможность получать механические поля для различного (близкого по свойствам к меди) материала, не проводя каждый раз заново решение анизотропной задачи, что порой при сложных граничных условиях и геометрии тела, составляет непростую задачу [4].