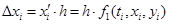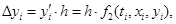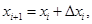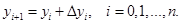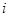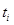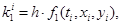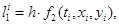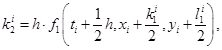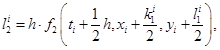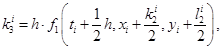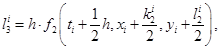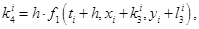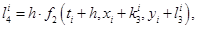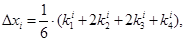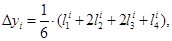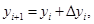Аналитическое решение той или иной прикладной задачи является чаще исключением в силу сложного и приближенного характера исследуемых моделей реальных процессов. В связи с этим численный анализ математический моделей является актуальным и эффективным аппаратом конструктивного исследования прикладных проблем. Численное решение решения задачи Коши для обыкновенного дифференциального уравнения первого порядка:
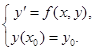
состоит в том, что на отрезке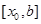 
вводится сетка 
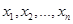узлов интегрирования. Для равномерной сетки 
, 
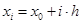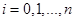, при этом величина 
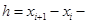шаг сетки (интегрирования). В узлах сетки интегрирования находятся приближенные значения 
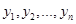точного решения 
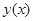. Результатом численного решения является таблица 
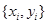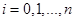, (сеточная функция) приближенных значений искомого решения 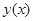в узлах сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом.
Метод Эйлера занимает ключевую позицию в теории численных методов интегрирования обыкновенных дифференциальных уравнений. Построение численного решения по методу Эйлера реализуется с помощью расчетной формулы [1]:
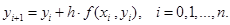(1)
Расчет ошибки метода Эйлера происходит путем разложения функции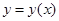 
в ряд Тейлора. В окрестности начальной точки имеем [1]:
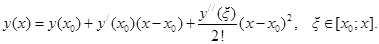
При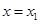 
:
,
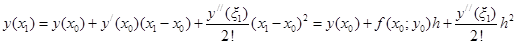или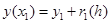 
, где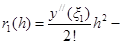 
остаточный член, 
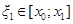, характеризующий локальную (шаговую) ошибку метода Эйлера, т.е. ошибку, совершаемую на одном шаге. При многократном применении формулы происходит наложение ошибок и образуется глобальная ошибка. Локальная ошибка 
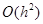метода Эйлера – это бесконечно малая величина от 
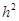, а глобальная 
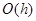– бесконечно малая от 
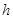. Следовательно, метод Эйлера имеет глобальную ошибку на каждом шаге на единицу по порядку хуже, чем локальная погрешность.
Существуют несколько способов построения численных методов решения задачи Коши более высокой по порядку относительно 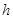точности. На практике наиболее распространен метод Рунге-Кутты четвертого порядка точности, в котором используется не линейная аппроксимация, а аппроксимация с помощью квадратурных формул Симпсона. Искомые значения 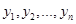на каждом шаге итерационного процесса последовательно вычисляются по формулам [1]:
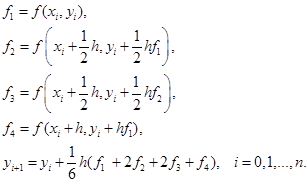(2)
Локальная погрешность метода Рунге-Кутты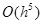 
– это бесконечно малая величина относительно 
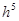, а глобальная 
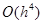– бесконечно малая от 
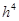. Таким образом, метод Рунге-Кутты является более точным по сравнению с методом Эйлера. Проиллюстрируем сравнение и применение данных численных методов решения задачи Коши на примере.
Пример. Решить дифференциальное уравнение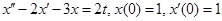 
на интервале 
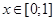с шагом 
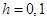методом Эйлера, методом Рунге-Кутты.
Решение. Проведем решение поставленной задачи в несколько этапов.
1. Найдем общее решение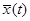 
линейного однородного дифференциального уравнений второго порядка (ЛОДУ) с постоянными коэффициентами:
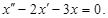
Сделаем замену: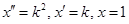 
. Тогда 
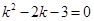– характеристическое уравнение ЛОДУ и 
, 
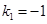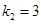. Следовательно, 
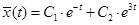– общее решение ЛОДУ.
2. Найдем частное решение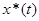 
данного линейного неоднородного дифференциального уравнений второго порядка (ЛНДУ) с постоянными коэффициентами:
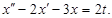
Определим вид частного решения. По условию правая часть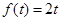 
. Тогда 
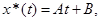где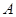 
, 
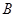– неопределенные коэффициенты. Для определения значений коэффициентов 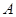, 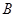вычислим производные: 
, 
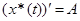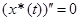и подставим их в данное уравнение: 
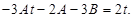Следовательно, 
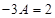и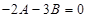 
откуда 
, 
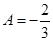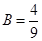и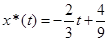 
– частное решение данного ЛНДУ.
3. По теореме [5] о структуре общего решения ЛНДУ получаем общее решение данного дифференциального уравнения: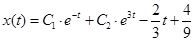 
.
4. Используя начальные условия: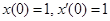 
определим значения 
:
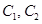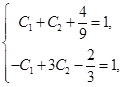
где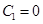 
, 
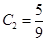. Следовательно, 
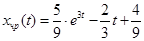– частное (точное) решение данной задачи Коши. В таблице 1 столбец 
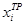содержит значения точного решения данного дифференциального уравнения в расчетных точках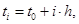 
.
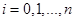5. Найдем численное решение методом Эйлера. Сведем данное дифференциальное уравнение второго порядка к системе дифференциальных уравнений. Для этого сделаем замену: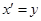 
, 
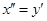. Тогда одновременно должны выполняться равенства
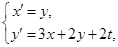
при этом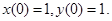 
Численное решение системы двух дифференциальных уравнений первого порядка с двумя искомыми функциями:
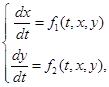(3)
где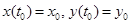 
, по методу Эйлера (1) для каждой неизвестной функции строится по формулам [1]:
|
|
|
|
|
|
В таблице 1 столбцы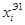 
, 
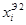содержат значения численных решений данного дифференциального уравнения, полученных методом Эйлера с шагом интегрирования 
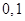и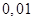 
соответственно.
Таблица 1
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0,1 |
1,128 |
1,1 |
1,124 |
1,128 |
|
2 |
0,2 |
1,323 |
1,25 |
1,315 |
1,323 |
|
3 |
0,3 |
1,611 |
1,465 |
1,593 |
1,611 |
|
4 |
0,4 |
2,022 |
1,765 |
1,99 |
2,022 |
|
5 |
0,5 |
2,601 |
2,174 |
2,547 |
2,601 |
|
6 |
0,6 |
3,405 |
2,726 |
3,318 |
3,405 |
|
7 |
0,7 |
4,515 |
3,464 |
4,377 |
4,514 |
|
8 |
0,8 |
6,035 |
4,443 |
5,823 |
6,034 |
|
9 |
0,9 |
8,111 |
5,736 |
7,789 |
8,11 |
|
10 |
1 |
10,936 |
7,437 |
10,455 |
10,935 |
Реализовать численное решение можно с помощью вычислительной техники, позволяющей проводить сложные расчеты с применением различных компьютерных программ. Достаточно удобной программой для обучения, вычислений и визуализации результатов математического моделирования инженерных расчетов является Mathcad [3]. В [4] приведены примеры документов Mathcad, реализующих алгоритм задачи Коши по методу Эйлера.
6. Найдем численное решение методом Рунге-Кутты. Сведем данное дифференциальное уравнение второго порядка к системе дифференциальных уравнений:
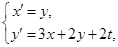
при этом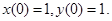
Численное решение системы (3) двух дифференциальных уравнений первого порядка с двумя искомыми функциями по методу Рунге-Кутты (2) строится для каждой функции отдельно по формулам [1]:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где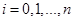 
. В таблице 1 столбец 
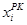содержит значения численного решения данного дифференциального уравнения, полученного методом Рунге-Кутты с шагом интегрирования 
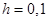. Вычисления можно реализовать в программе Mathcad с помощью команды 
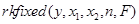[4].
6. По данным таблицы 1 на рис. 1 представим совместное графическое решение данного дифференциального уравнения рассмотренными методами. В силу своей наглядности графическое решение может способствовать актуализации познавательного интереса обучающихся, а значит обеспечению условий, направленных на формирование и поддержку мотивов учения у студентов [2].
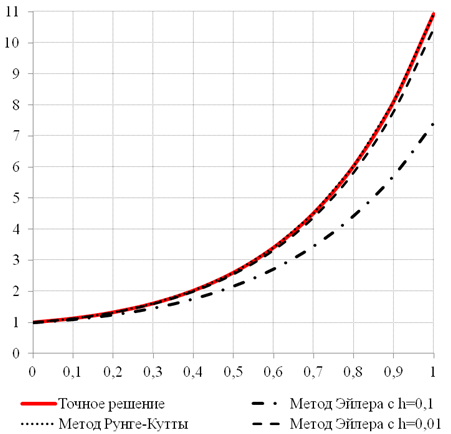
Рис. 1. Совместное графическое решение
Таблица 2
|
|
|
Абсолютные погрешности |
Относительные погрешности (%) |
||||
|
|
|
|
|
|
|
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0,1 |
0,028 |
0,004 |
0 |
2,482 |
0,355 |
0 |
|
2 |
0,2 |
0,073 |
0,008 |
0 |
5,518 |
0,605 |
0 |
|
3 |
0,3 |
0,146 |
0,018 |
0 |
9,063 |
1,117 |
0 |
|
4 |
0,4 |
0,257 |
0,032 |
0 |
12,71 |
1,583 |
0 |
|
5 |
0,5 |
0,427 |
0,054 |
0 |
16,417 |
2,076 |
0 |
|
6 |
0,6 |
0,679 |
0,087 |
0 |
19,941 |
2,555 |
0 |
|
7 |
0,7 |
1,051 |
0,138 |
0,001 |
23,278 |
3,056 |
0,022 |
|
8 |
0,8 |
1,592 |
0,212 |
0,001 |
26,379 |
3,513 |
0,017 |
|
9 |
0,9 |
2,375 |
0,322 |
0,001 |
29,281 |
3,97 |
0,012 |
|
10 |
1 |
3,499 |
0,481 |
0,001 |
31,995 |
4,398 |
0,009 |
7. Рассчитаем абсолютную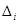 
и относительную 
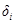погрешности метода Эйлера и метода Рунге-Кутты для каждого шага 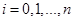соответственно по формулам [1]:
, 
,
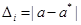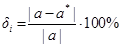где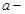 
точное значение величины, 
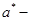приближенное значение величины. Значения погрешностей представлены в таблице 2.
Сравнивая значения абсолютных и относительных погрешностей вычислений из таблицы 2, а также с помощью рис. 1, делаем вывод о том, что более точными являются вычисления по методу Рунге-Кутты четвертого порядка точности. Повысить точность метода Эйлера можно, уменьшив шаг интегрирования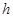 
.
Таким образом, в работе описаны основные численные методы решения задачи Коши для обыкновенных дифференциальных уравнений: метод Эйлера и метод Рунге-Кутты. Сравнительный анализ и оценка погрешностей данных численных методов реализованы на примере решения задачи Коши для обыкновенного дифференциального уравнения второго порядка. Аналитическое и численные решения данной задачи Коши выписаны в явном виде. Составлены таблицы абсолютных и относительных погрешностей вычислений на каждом шаге интегрирования. Для наглядности сравнения результатов вычислений представлено совместное графическое решение данной задачи всеми рассмотренными методами.