Постановка задачи
Тестирование учебных достижений студентов распространено в ВУЗах повсеместно. «Компетентностный подход», закрепленный федеральными государственными нормативными правовыми актами и стандартами, фиксирует важную роль тестируемых достижений, и систематическое тестирование занимает важное место в деятельности студентов, преподавателей и администрации, для него привлекаются значимые ресурсы.
В структуре Уральского государственного университета путей сообщения (УрГУПС) имеется постоянно действующий Центр тестирования (ЦТ) с основным залом на 100 компьютеризированных мест, специально предназначенный для проведения тестовых процедур. Основной способ организации тестирования предполагает резервирование некоторого количества мест, соответствующего количеству направляемых в ЦТ студентов, на период 105 минут, соответствующий паре занятий и двум переменам в общевузовской сетке расписания. Это гарантирует студенту возможность явиться в ЦТ в составе своей учебной группы, занять без очереди свое место и выполнить задание, вовремя вернувшись к другим учебным занятиям. Однако, очевидно, что количество студентов, которых может обслужить ЦТ в таком режиме, достаточно ограничено, а компьютеры большую часть времени (после окончания индивидуального теста до следующего группового захода) простаивают.
В период массового тестирования приходится привлекать дополнительные ресурсы в виде небольших компьютерных классов и труда квалифицированных преподавателей из числа доцентов и профессоров для наблюдения за порядком при тестировании. Возникает интерес к альтернативным способам организации тестирования в ЦТ (может быть, не столь удобным для организованных в учебные группы студентов), и сравнительной оценке его пропускной способности, а также комбинированным решениям, ориентированным на разные потребности студентов. Для этого применяются методы сбора и обработки статистической информации и математического моделирования, результаты представлены в данной работе.
Дизайн исследования
Первоначально предполагалось: а) статистическими методами выявить обобщенные характеристики (среднее, дисперсию) продолжительности индивидуального тестирования; б) рассмотреть и сравнить по производительности модельную ситуацию реализации индивидуальных тестов с аналогичным временем при условии случайной явки студентов, то есть при организации тестирования по живой очереди, с помощью математического аппарата «Теории очередей». Этот раздел теории вероятностей известен в отечественной литературе как «теория массового обслуживания» [1] и широко используется в качестве инструмента прогнозирования для таких систем [4], [5]. В результате реализации этой программы были получены некоторые практически значимые результаты и выявлен сложный характер распределения продолжительности индивидуального тестирования, что привело к пониманию необходимости дальнейших исследований. Вычисления проводились с помощью процессора электронных таблиц MS Excel.
1. Распределения величин, характеризующих процесс тестирования
На первом этапе были использованы фактические данные о 2,2 тыс. индивидуальных тестов из 190 протоколов тестирования, проведенных преподавателями УрГУПС с помощью Единого портала интернет-тестирования в сфере образования [3]: время начала и окончания теста, количество заданий в тесте и назначенное на тест преподавателем время. Были определены продолжительности индивидуальных тестов и отношения этих продолжительностей к количеству заданий в тесте, то есть оценка среднего времени, использованного студентом для ответа на единичное задание к тесте. Указанные величины имеют случайный характер, поэтому для их изучения были построены статистические распределения.
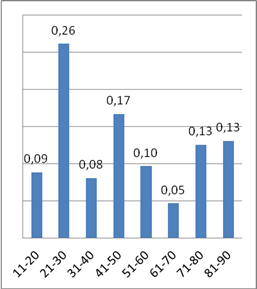
Назначенная продолжительности теста имеет распределение сложного вида. В подавляющем количестве случаев это значение от 10 до 90 минут. Наблюдаются максимумы в районе 30 и 45 минут, которые можно интерпретировать психологическими факторами. Последние столбцы соответствуют тестам остаточных знаний проекта ФЕПО, где время тестирования фиксировано и не может меняться по усмотрению преподавателя, организующего тест.
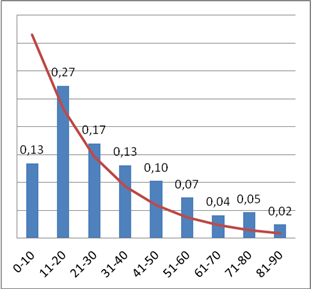
Фактическая продолжительность теста демонстрирует распределение, имеющее более плавную форму по сравнению с предыдущим. Характерно спадание вероятности наблюдения больших значений. Однако очевидны значительные отклонения этого распределения от показательного закона (на графике изображен кривой линией), что подтверждается применением статистических процедур: наблюдается существенный минимум вероятности в первой категории, а остальные категории заполнены больше, чем предсказано. Такие отклонения приводят, в дальнейшем, к некоторым сомнениям в правомерности применения математического аппарата «Теории очередей» для математического моделирования работы Центра тестирования.
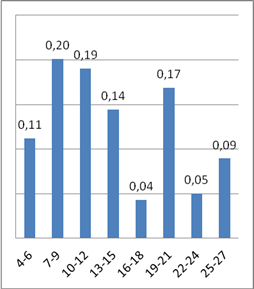
По количеству заданий теста выделяется основная группа первых четырех категорий (4–15 заданий), охватывающая 2/3 рассмотренных случаев, а пятой категории (16–18 заданий) соответствует заметный минимум распределения. Большие по количеству заданий тесты (19–27 заданий) отражают использование ФЕПО, где возможности выбора заданий ограничены. Таким образом, количество заданий теста – более удобная для анализа характеристика по сравнению с назначенным преподавателем временем тестирования. На основании таких особенностей распределения принято решение в дальнейшей работе сконцентрировать внимание на массовой ситуации и провести математическое моделирование для случаев 4–15 заданий. Среднее значение фактической продолжительности индивидуального теста для этой группы оказалось равным 22 минуты.
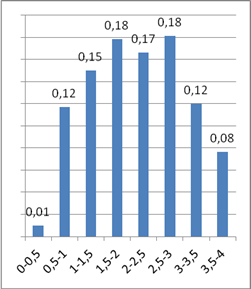
Среднее время на единичное задание, (точнее, отношение фактического времени тестирования к количеству заданий) имеет распределение наиболее простого вида по сравнению с другими производными характеристиками. Это подтверждает предыдущий вывод о преимуществе «количества заданий» над «назначенным временем тестирования» при анализе данных. Ещё заметим, что время на тест определяется в режиме интернет-тренажера из расчета 2 минуты на задание (но может быть увеличено по решению преподавателя); с этим, скорее всего, связан небольшой локальный минимум вероятности, соответствующий категории 2–2,5 минут.
Подводя промежуточные итоги, отметим, что средняя продолжительность индивидуального тестирования в массовой группе случаев до 15 заданий составляет 22 минуты, а с учетом потерь времени на начало теста и фиксацию результата, среднее время обслуживания студента в ЦТ можно принять приближенно равным 0,5 часа.
2. Аналитическое моделирование работы ЦТ как системы массового обслуживания
На втором этапе исследования была использована модель открытой СМО с N каналами обслуживания и неограниченной очередью в форме марковской цепи специального вида с бесконечным числом состояний, соответствующих количеству занятых мест в ЦТ и очереди

В соответствии с [1, 2], стационарная (по эргадической теореме, она совпадает с предельной) вероятность начального (нулевого) состояния этой марковской цепи может быть найдена из соотношения
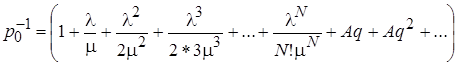 ,
, 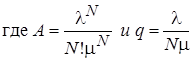
Используя известную формулу для ряда геометрической прогрессии, для слагаемых суммы, соответствующих очереди, получаем
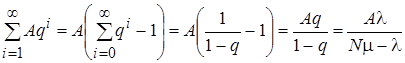
Что позволяет преобразовать исходное выражение
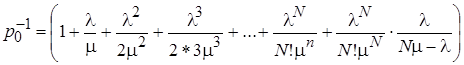
Таким образом, наличие неограниченной очереди без включения в работу новых каналов обслуживания оказывает на вероятность начального состояния такое же влияние, как единственное состояние с 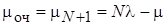 и в дальнейшей работе были использованы марковские цепи, соответствующие графу (при разном значении N)
и в дальнейшей работе были использованы марковские цепи, соответствующие графу (при разном значении N)


С помощью этой модели определяются вероятности всех состояний, отражающие заполненность ЦТ и вероятность очереди в зависимости от двух параметров: интенсивности входящего потока студентов λ и среднего времени обслуживания одного студента, присутствующей в модели в виде номинальной интенсивности обслуживания заявок одним каналом  . По результатам первого этапа исследования, среднее время обслуживания студента составило 0,5 часа, поэтому было принято значение µ=2 человека в час. Собственно, расчетный алгоритм для вероятностей состояний марковской цепи включает три шага: предварительное рекуррентное вычисление коэффициентов
. По результатам первого этапа исследования, среднее время обслуживания студента составило 0,5 часа, поэтому было принято значение µ=2 человека в час. Собственно, расчетный алгоритм для вероятностей состояний марковской цепи включает три шага: предварительное рекуррентное вычисление коэффициентов 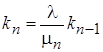 при
при 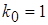 и
и 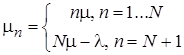 ; суммирование этих коэффициентов для определения вероятности начального состояния
; суммирование этих коэффициентов для определения вероятности начального состояния 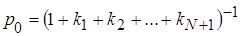 ; итогового определения вероятностей всех состояний СМО
; итогового определения вероятностей всех состояний СМО 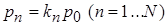 и вероятности очереди
и вероятности очереди 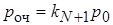 .
.
Для получения практически значимых результатов был поставлен вопрос о пропускной способности ЦТ с разным количеством эксплуатируемых мест N = 10, 20, … 100. В природе модели заложена ненулевая вероятность очереди при любой интенсивности входного потока, поэтому, для конкретности, удовлетворительной работой ЦТ было решено считать случаи с вероятностью очереди меньше 10% и сконцентрировать внимание на поиске таких значений λкр(N), при которых вероятность очереди составила ровно 10%. Расчетный алгоритм (для каждого значения N) с варьируемыми значениями λ и μ был реализован на листе MS Excel, после чего ячейке, выделенной для μ, было присвоено значение 2, а значение λ подбиралось, исходя из условия роч=0,1. Полученная зависимость представлена на следующем графике.
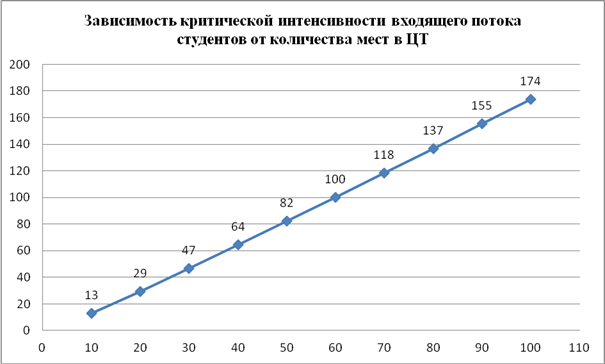
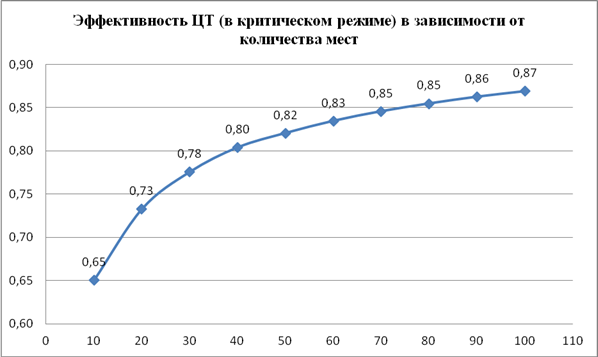
С помощью такого графика можно легко ответить на вопрос, сколько мест в ЦТ требуется задействовать для обслуживания живой очереди студентов известной интенсивности (с учетом безвозвратных потерь времени при простое машин), например, для обслуживания входящего потока с интенсивностью 100 человек в час оказывается достаточно 60 мест.
Пропускная способность ЦТ варьируется с 13 человек в час (при использовании 10 мест) до 174 человек в час (при использовании 100 мест), хотя номинальная производительность каждого места составляет 2 человека в час и, с учетом количества мест, должна достигать 200 человек в час. Отношения производительности ЦТ к количеству мест, показанные на следующем графике, демонстрируют, что с увеличением количества каналов обслуживания (мест) он работает эффективней и доля безвозвратных потерь компьютерного времени, связанная со стохастичностью входного потока, заметно снижается, достигая 13% при эксплуатации 100 мест.
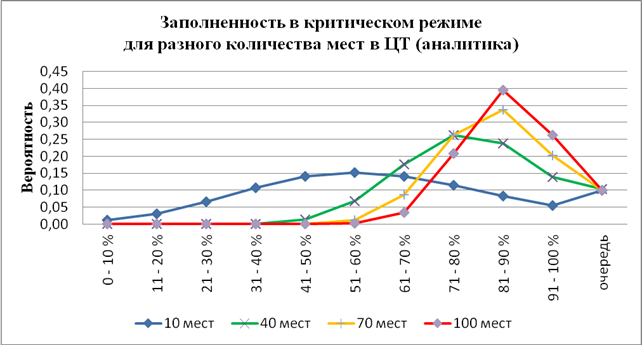
Для более глубокого понимания этого эффекта сравним относительную заполненность ЦТ в виде распределений вероятности, при разных количествах мест. Характерные графики, приведённые ниже, демонстрируют, что увеличение количества мест сопровождается заметным смещением максимума в распределении занятых мест вправо, что объясняет соответствующее возрастание эффективности использования ЦТ.
Основные выводы
1. Выяснилось, что резервирование машинного времени (по 1,5 часа на студента) позволяет достичь интенсивности в 2 – 3 раза меньшей, чем работа в режиме «живой очереди» на том же количестве компьютеров. Групповое тестирование при количестве заданий больше 15 необходимо, всё же, проводить «по записи» для совмещения с сеткой расписания, с учетом прогнозируемого трафика: места, невостребованные для более производительного режима работы, могут быть отданы организованным группам тестируемых.
2. Полученные в проведенном исследовании зависимость λкр(N) позволяет, при привлечении данных о трафике в ЦТ, определять количество мест, которые можно выделить для тестирования организованных групп без существенного ущерба для более производительной работы «по живой очереди», а выработанная техника расчета – корректировать аналитическую модель с учетом уточняемых в опыте параметров.
3. Для более глубокого влияния отклонений входного потока заявок от показательного закона на производительность ЦТ надо предпринять имитационное моделирование исследуемого процесса, к чему мы вернемся в дальнейшей публикации.
4. Работа ЦТ была рассмотрена как квазистационарный процесс, переходные эффекты, возникающие при изменении трафика в ЦТ, считаются несущественными. Вне внимания так же остались вопросы работы персонала ЦТ по распределению большого количества студентов по компьютерным местам и фиксации результатов теста, влияние неравномерностей входящего потока студентов, налагаемых расписанием занятий.

