Введение
Любые решения, принимаемые в настоящем, приведут к результатам и последствиям только в будущем, при этом достоверно и точно спрогнозировать к какому именно результату приведет принятое ранее решение практически невозможно. Помимо проблемы неопределенности и непредсказуемости будущего необходимо принимать во внимание и тот факт, что в любом процессе принятия решения в значительной степени присутствует человеческие фактор, который оказывает влияние на окончательное решение лица, принимающего решение (ЛПР): выбор критериев, наилучшей, для данного ЛПР, альтернативы, вынесение суждений и оценок, и пр. Психология вынесения суждений и оценок человеком [9], свидетельствует о том, что как суждения, так и оценки даются не в точечном, а интервальном виде [2, 3, 5]. При этом любое значение оценки внутри интервала ее изменения равновероятно, то есть имеют равномерное распределение вероятностей. Поэтому модель интервально неопределенных оценок является интервально стохастической и представляет собой случайные равномерно распределенные величины в интервале своего изменения [1, 3, 6].
Среди большого количества существующих методов принятия многокритериальных решений [1], метод аналитической иерархии (МАИ) является на сегодняшний день наиболее универсальным и научно обоснованным методом, позволяющим принимать наилучшие решения при многих критериях как качественных, так и количественных [7]. Однако классический метод МАИ [1, 4, 8] имеет дело лишь с однозначными, точечными оценками и не позволяет принимать решение в условиях интервальной неопределенности суждений и оценок, отвечающей психологии вынесения оценок и суждений человеком..
В статье рассматривается интервально стохастический метод аналитической иерархии (ИС-МАИ), развитый в работах проф. А.Г. Мадеры [3, 5], позволяющий принимать наилучшие решения в многокритериальных проблемах при интервально стохастической неопределенности суждений и оценок. Применение метода продемонстрировано на конкретной многокритериальной неопределенной проблеме принятия решения о закупке руководством фирмы грузового автомобиля.
Интервально стохастический метод аналитической иерархии ИС-МАИ
Теоретическое обоснование метода ИС-МАИ приведено в [3], детерминированный классический метод МАИ – в [1, 4, 8]. Алгоритм применения метода ИС-МАИ для произвольной матрицы попарных сравнений содержит следующие шаги:
1. Строится интервально стохастическая матрица попарных сравнений (оценок критериев и сравниваемых альтернатив по каждому критерию), вида:
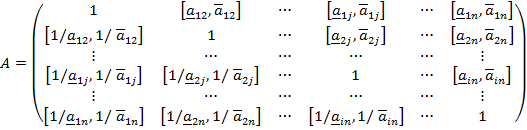 .
.
где 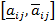 - интервальная оценка значимости фактора по фундаментальной шкале [1, 3];
- интервальная оценка значимости фактора по фундаментальной шкале [1, 3]; 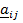 и
и 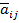 - нижняя и верхняя границы интервала изменения. Оценки в матрице попарных сравнений являются статистически независимыми равномерно распределенными случайными величинами
- нижняя и верхняя границы интервала изменения. Оценки в матрице попарных сравнений являются статистически независимыми равномерно распределенными случайными величинами 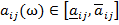 ,
, 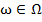 , где
, где 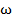 - элементарные события из пространства элементарных событий
- элементарные события из пространства элементарных событий 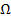 [7].
[7].
2. Определение нормированных статистических мер (математических ожиданий (МО), дисперсий (Д), среднеквадратических отклонений СКО)) элементов 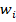 собственных векторов
собственных векторов 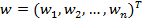 , или векторов приоритетов (коэффициентов важности):
, или векторов приоритетов (коэффициентов важности):

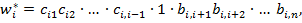
- если элемент в столбце 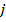 и -й строке матрицы А имеет вид [
и -й строке матрицы А имеет вид [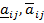 ], то компонент в произведении
], то компонент в произведении 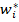 равен
равен
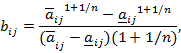
- если элемент в столбце 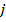 и
и 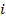 -й строке матрицы А имеет вид
-й строке матрицы А имеет вид 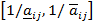 , то компонент
, то компонент 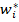 в произведении равен
в произведении равен
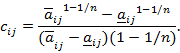

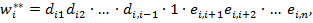
- если элемент в столбце 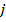 и -й строке матрицы А имеет вид [
и -й строке матрицы А имеет вид [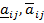 ], то компонент в
], то компонент в 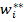 произведении равен
произведении равен
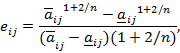
- если элемент в столбце 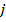 и
и 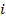 -й строке матрицы А имеет вид [
-й строке матрицы А имеет вид [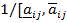 ], то компонент
], то компонент 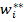 в произведении равен
в произведении равен
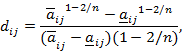

3. Определение нормированных МО, Д и СКО векторов приоритетов для критериев и альтернатив по каждому критерию.
В точечном детерминированном методе МАИ [8] составляются несколько матриц попарного сравнения: одна матрица (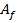 ) для критериев
) для критериев 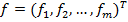 и m матриц (
и m матриц (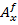 ) для альтернатив
) для альтернатив 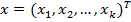 относительно каждого критерия из вектора
относительно каждого критерия из вектора 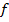 . Затем для каждой матрицы попарных сравнений критериев определяются их собственные векторы, являющиеся векторами приоритетов критериев
. Затем для каждой матрицы попарных сравнений критериев определяются их собственные векторы, являющиеся векторами приоритетов критериев 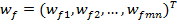 и векторами приоритетов альтернатив
и векторами приоритетов альтернатив 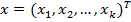 относительно каждого критерия
относительно каждого критерия 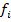 (
(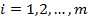 ), то есть
), то есть 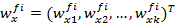 .
.
В рассматриваемом интервально стохастическом методе Мадеры ИС-МАИ, в отличие от классического МАИ, элементы матриц попарных сравнений являются интервально стохастическими и имеют случайные собственные векторы. Вычислим их статистические меры - МО по (1), Д по (2) и СКО по (3) - для векторов приоритетов критериев 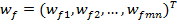 :
: 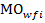 ,
, 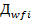 ,
, 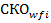 , и векторов приоритетов альтернатив
, и векторов приоритетов альтернатив 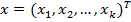 относительно каждого критерия
относительно каждого критерия 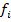 (
(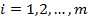 ), то есть
), то есть 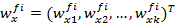 :
: 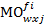 ,
, 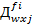 ,
, 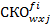 .
.
4. Определение нормированных МО, Д и СКО для вектора глобальных приоритетов альтернатив каждой альтернативы (решения).
Значения глобальных приоритетов (ГП) альтернатив в детерминированном МАИ [8], по величине которых производится окончательный выбор наилучшего решения в многокритериальной проблеме, вычисляются как сумма произведений приоритетов данной альтернативы относительно каждого критерия на приоритеты соответствующих критериев.
В интервально стохастическом методе Мадеры (ИС-МАИ) приоритеты как критериев 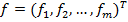 , так и альтернатив
, так и альтернатив 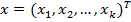 относительно каждого критерия
относительно каждого критерия 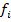 (
(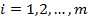 ), то есть
), то есть 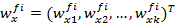 , представляют собой случайные величины. Поэтому глобальные приоритеты
, представляют собой случайные величины. Поэтому глобальные приоритеты 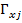 альтернатив
альтернатив 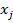 (
(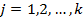 ) также будут случайными и независимыми между собой. Вычислим их статистические меры:
) также будут случайными и независимыми между собой. Вычислим их статистические меры: 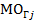 , и
, и 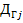 ,
, 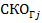 (
(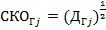 ):
):
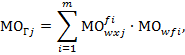
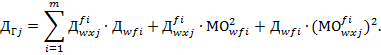
5. По вычисленным значениям 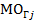 ,
, 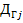 и
и 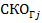 для значений
для значений 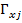 относительно каждой альтернативы
относительно каждой альтернативы 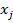 (
(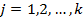 ), строятся
), строятся 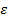 -интервалы, внутри которых с доверительной вероятностью
-интервалы, внутри которых с доверительной вероятностью 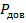 будут лежать значения ГП, а именно,
будут лежать значения ГП, а именно, 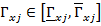 . При этом нижние и верхние границы
. При этом нижние и верхние границы 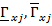 интервалов ГП альтернатив
интервалов ГП альтернатив 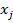 равны
равны 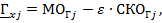
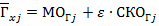 , или значения
, или значения 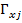 для альтернативы
для альтернативы 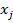 заключены в интервале
заключены в интервале 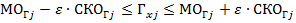 . Целесообразно выбирать
. Целесообразно выбирать 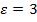 , при котором вероятность обнаружить ГП вне
, при котором вероятность обнаружить ГП вне 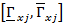 менее 0,1 [7].
менее 0,1 [7].
6. Построение диаграммы интервальных глобальных приоритетов и принятие наилучшего решения в интервально стохастическом методе Мадеры (ИС-МАИ) [3, 5].
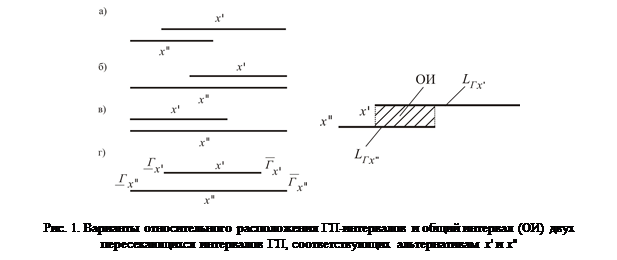
Полученные в п. 5 интервалы возможных значений ГП служат для выбора наилучшей альтернативы, который осуществляется посредством анализа относительного расположения нижних и верхних границ интервалов ГП различных альтернатив. Целесообразно выбирать такое интервальное решение, для которого нижняя и верхняя границы интервала ГП имеют максимальные значения среди границ интервалов ГП других альтернатив. Так, на рис. 1,а таковым является интервал ГП альтернативы x'. Худшей будет альтернатива x' (рис. 1,а), для которой границы ГП минимальны и сдвинуты влево. Сказанное справедливо и для тех случаев, когда у двух сравниваемых между собой ГП-интервалов совпадают либо верхняя (рис. 1,б), либо нижняя (рис. 1,в) границы. Так, если верхние границы двух интервалов ГП совпадают, то выбирается то решение, у которого значение нижней границы больше (x', рис. 1,б), а если нижние границы ГП совпадают, то лучшим будет решение с большим значением верхней границы (x'', рис. 1,в). Когда у двух альтернатив нижняя и верхняя границы совпадают, то оба решения равноценны по всем критериям и принятие одного из них определяется только мнением и пристрастиями ЛПР.
7. Оценка интервальной устойчивости альтернатив.
Ввиду того, что наилучшее решение в интервально стохастическом АНР определяется на основании интервальных оценок, необходимо также оценить устойчивость интервальной альтернативы [3, 5], которая характеризует область интервала ГП, в пределах которой принятое решение остается неизменным, а при выходе за ее пределы области (оставаясь внутри ГП-интервала) изменяется на иное решение (рис. 1). Интервальная устойчивость альтернативы 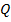 (
(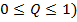 определяется как
определяется как 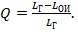 Если
Если 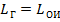 , то интервальная устойчивость данной альтернативы
, то интервальная устойчивость данной альтернативы 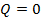 и данная альтернатива в границах внутри ОИ будет ничем не лучше другой. Когда интервалы ГП двух альтернатив не пересекаются, длина
и данная альтернатива в границах внутри ОИ будет ничем не лучше другой. Когда интервалы ГП двух альтернатив не пересекаются, длина 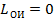 , интервальная устойчивость обеих альтернатив будет максимальной и равной
, интервальная устойчивость обеих альтернатив будет максимальной и равной 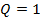 . Вообще, чем больше
. Вообще, чем больше 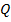 у данной альтернативы, тем в большем диапазоне ГП-интервала она будет сохранять свое преимущество перед остальными. И наоборот, чем
у данной альтернативы, тем в большем диапазоне ГП-интервала она будет сохранять свое преимущество перед остальными. И наоборот, чем 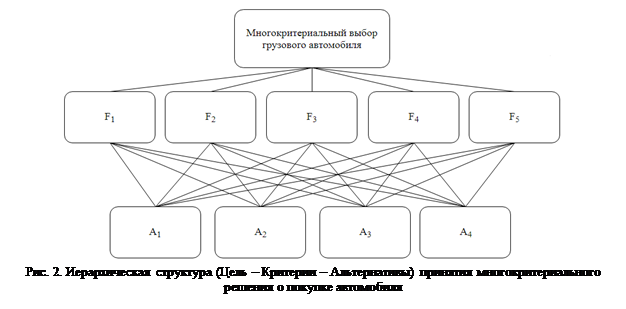 меньше величина
меньше величина 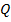 альтернативы, тем меньше у нее преимуществ перед другими и она может быть заменена другой альтернативой.
альтернативы, тем меньше у нее преимуществ перед другими и она может быть заменена другой альтернативой.
Применение метода для многокритериального выбора грузового автомобиля
Логистическая компания планирует расширить парк седельных тягачей с колесной формулой 4×2 и с этой целью намеревается приобрести новый грузовой автомобиль, руководствуясь пятью критериями: 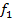 – цена автомобиля, руб;
– цена автомобиля, руб; 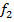 – средний расход топлива на 100 км;
– средний расход топлива на 100 км; 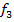 – подверженность деталей износу;
– подверженность деталей износу; 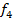 – вероятность поломки;
– вероятность поломки; 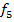 – максимально нагрузка (максимальное количество тонн продукта, которое машина может перевезти за 1 рейс). Критерий
– максимально нагрузка (максимальное количество тонн продукта, которое машина может перевезти за 1 рейс). Критерий 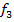 должен принимать как можно большее значение, критерии
должен принимать как можно большее значение, критерии 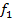 ,
, 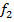 ,
, 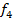 ,
, 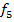 – меньшие. Рассматриваемые альтернативы: Volvo (
– меньшие. Рассматриваемые альтернативы: Volvo (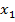 ); Scania (
); Scania (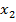 ); МАЗ (
); МАЗ (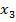 ); Mercedes (
); Mercedes (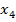 ).
).
Интервальные матрицы попарных сравнений важности критериев 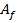 и альтернатив
и альтернатив 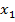 ,
, 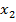 ,
, 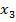 ,
, 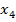 по каждому критерию
по каждому критерию 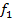 ,
, 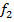 ,
, 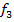 ,
, 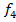 ,
, 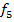 , то есть
, то есть 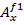 ,
, 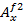 ,
, 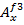 ,
, 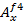 , имеют вид.
, имеют вид.
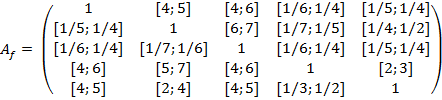
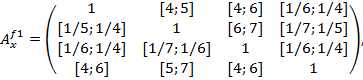
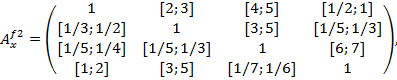
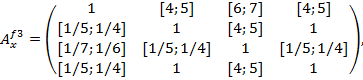
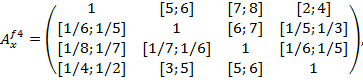
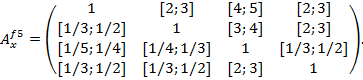
Вычисления по вышеизложенной методике приводят в следующим интервалам ГП:
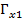 ∈ [0,397; 0,516];
∈ [0,397; 0,516]; 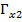 = ∈ [0,113; 0,141];
= ∈ [0,113; 0,141]; 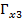 = ∈ [0,108; 0,141];
= ∈ [0,108; 0,141]; 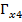 = ∈ [0,134; 0,177].
= ∈ [0,134; 0,177].
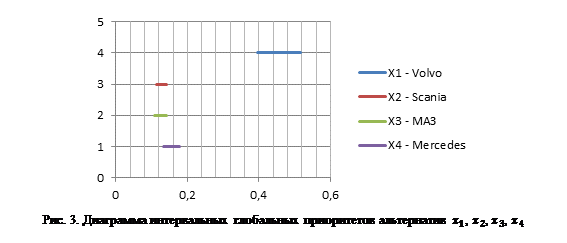
Из диаграммы интервальных глобальных приоритетов (рис. 3) следует, что левая и правая границы ГП-интервала альтернативы 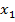 принимают наибольшие значения и поэтому является наилучшей. Таким образом, основываясь на интервально методе Мадеры ИС-МАИ руководству компании следует купить грузовой автомобиль марки Volvo. Кроме того, ГП-интервал альтернативы
принимают наибольшие значения и поэтому является наилучшей. Таким образом, основываясь на интервально методе Мадеры ИС-МАИ руководству компании следует купить грузовой автомобиль марки Volvo. Кроме того, ГП-интервал альтернативы 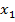 не пересекается с ГП-интервалами других альтернатив (рис. 3), поэтому интервальная устойчивость у
не пересекается с ГП-интервалами других альтернатив (рис. 3), поэтому интервальная устойчивость у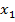 максимальна
максимальна 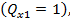 что также свидетельствует в пользу выбора альтернативы
что также свидетельствует в пользу выбора альтернативы 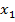 .
.
Заключение
В статье рассмотрен алгоритм применения на практике интервально стохастического метода ИС-МАИ [3, 5], позволяющего принимать наилучшие, научно обоснованные решения в многокритериальных проблемах при неопределенности оценок и суждений ЛПР. В отличие от классического метола МАИ [8], в методе ИС-МАИ учитывается психология принятия решений и вынесения субъективных суждений и оценок, присущих человеку, что существенно повышает достоверность принятия многокритериальных решений. А введенные в [3, 5] диаграммы интервальных глобальных приоритетов альтернатив и интервальная устойчивость, позволяют принимать наилучшее, обладающее максимальной устойчивостью к замене его другим, многокритериальное решение. Применение метода рассмотрено на примере многокритериальной проблемы выбора грузового автомобиля.
Выражаю благодарность своему научному руководителю профессору, доктору наук Мадере А.Г. за постановку задачи, руководство и обсуждение полученных результатов.

