Постановка задачи. В телешоу участвует один игрок и ведущий. Перед игроком представлены три закрытые двери, за двумя из которых находятся козы, а за оставшейся − автомобиль. Задача игрока угадать дверь за которой находится автомобиль.[4]
Например, игрок выбирает одну из трех дверей, после чего ведущий, который знает, где находятся козы и автомобиль, открывает одну из двух дверей с козой. Тем самым перед игроком будут представлены не три двери, как изначально, а уже две. Возникает вопрос: "Стоит ли игроку изменить свой первоначальный выбор?".
Чтобы обосновать задачу математически, применим аппарат теории вероятностей, решим ее, используя следствия формулы полной вероятности (1) − формулу для переоценки гипотез – формулу Байеса (2).[1],[2]
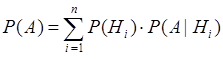 , (1)
, (1)
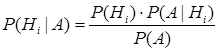 (2)
(2)
где событие А = {выигрыш автомобиля}, n = 2, гипотезы: H1 = {первоначальный выбор не был изменен}, H2 = { изменили первоначальный выбор}, условные вероятности: P(A|H1) − условная вероятность того, что будет выигран автомобиль, при первоначальном выборе, P(A|H2) − условная вероятность того, что будет выигран автомобиль при смене первоначального выбора.![]()
Рассмотрим парадокс Монти Холла для случая с тремя дверями. [4] Схематично данную ситуацию иллюстрирует рис.1
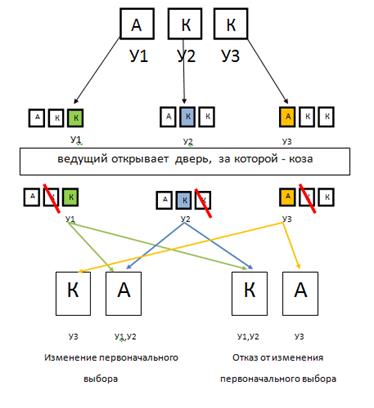
рис.1. Дерево принятия решений для трех дверей
Найдем вероятность наступления события А, если произошла одна из гипотез
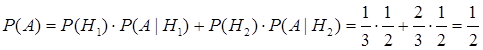 .
.
Вероятность того, что, не меняя свой выбор, можно выиграть автомобиль, равна 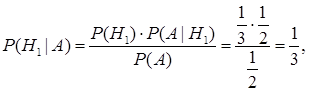
а вероятность того, что при смене выбора, можно выиграть автомобиль, равна 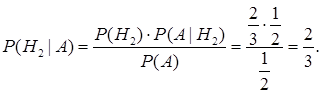
Для случая с тремя дверями была проведена симуляция парадокса Монти Холла с помощью программирования в Microsoft Excel.[3],[5]
Выполнено 1000 итераций. Чем больше раз повторять эксперимент, тем точнее результат покажет 333 шанса на выигрыш, если придерживаться первоначального выбора и 667 шансов на победу при изменении решения. Фрагмент работы программы представлен на рис.2.
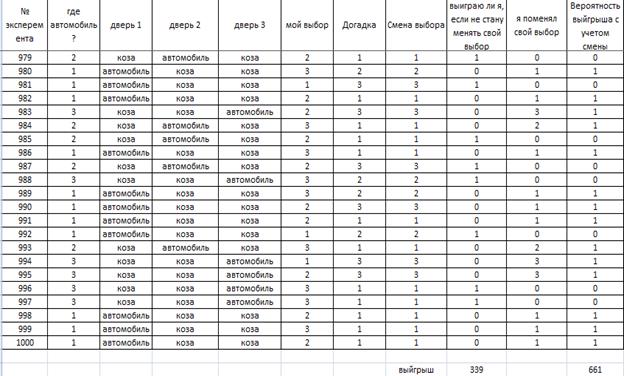
рис.2. Программа парадокса Монти Холла для трёх дверей в Excel
Таким образом, игроку следует изменить свой первоначальный выбор т. к вероятность выигрыша в этом случае будет в два раза выше в отличие от того, если же он не изменит свой выбор.
Анализ случая увеличения числа дверей.
Формулировка соответствующей задачи остается без изменения, единственное изменение – число дверей, открытых ведущим. Так для случая четырех дверей (рис. 3) ведущий должен открывать две двери (за которыми находятся козы), в случае пяти дверей (рис. 5) − три, и так далее, чтобы всегда оставалась одна неоткрытая дверь кроме той, которую изначально выбрал игрок. И это, возможно, будет некоторой подсказкой для игрока, чтобы изменить первоначальный выбор. Если ведущий будет открывать меньшее количество дверей, то задача уже не будет аналогична оригинальной задаче Монти Холла.
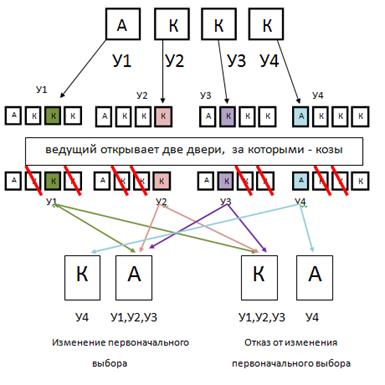
рис.3. Дерево принятия решений для четырёх дверей
Проведем математический расчет.[1],[2]
![]() .
.
Вероятность того, что, автомобиль выигран без смены двери, равна 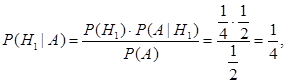
а вероятность того, что при смене выбора можно выиграть автомобиль, равна 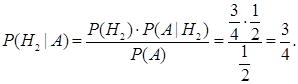
Помимо математического обоснования, была составлена экспериментальная модель, используя программу Microsoft Excel, для случая четырех дверей. [4], [5]
Для наглядности и удобства совершено 1000 экспериментов. Фрагмент работы программы представлен на рис.4.
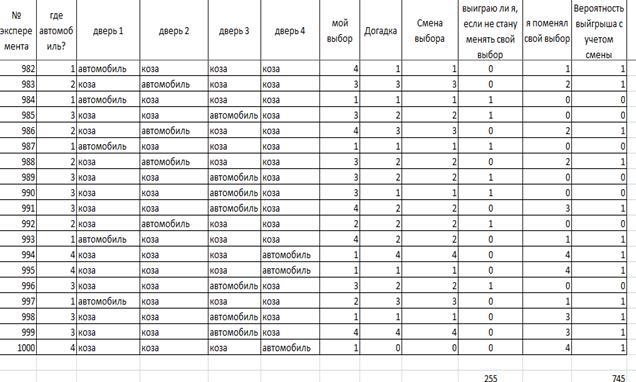
рис.4. Программа парадокса Монти Холла для четырёх дверей в Excel
Как видно, вероятность выигрыша не изменив первоначальный выбор, будет составлять 255 случаев из 1000, что составляет около 25% от общего количества. А если же игрок изменит свой первоначальный выбор, то вероятность выигрыша составит 745 случаев из 1000, что составляет 75% . Чем больше раз повторять эксперимент, тем точнее результат покажет 250 шансов на выигрыш, если придерживаться первоначального выбора и 750 шансов на победу при изменении решения.
Представим схему и математические вычисления [1] для случая пяти дверей.
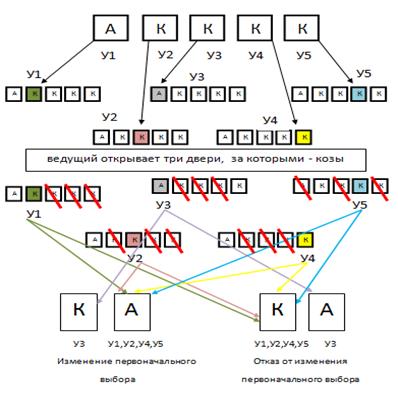
рис.5. Дерево принятия решений для пяти дверей
Вероятность того, что автомобиль выигран без смены двери, равна 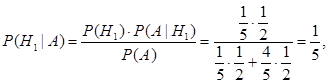
а вероятность того, что при смене выбора можно выиграть автомобиль, равна 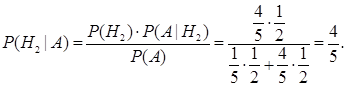
Вывод. Математически обосновав решение задачи Монти Холла и, проведя наглядный эксперимент, можно сказать, что все-таки нужно изменять свой первоначальный выбор, ибо вероятность успеха будет значительно больше.
Знание рассмотренного парадокса позволяет, например, грамотно взглянуть на спортивные стратегии, ставки и прогнозы для успешной игры в букмекерской конторе онлайн, чтобы угадать исход спортивного события.
Парадоксальность ситуации: кажется, что всё происходящее случайно, нет никакой разницы, поменяете вы своё решение или нет, но это не так. Конечно, у Вас остаётся шанс проиграть, но, тем не менее, смена выбора в условиях частичной осведомлённости увеличивает ваши шансы на выигрыш!

