Фондовый рынок как часть финансового рынка – место, где контрагенты имеют возможность продать и купить долгосрочные долговые и долевые ценные бумаги. Роль данного рынка заключается в концентрации и направлении сбережений от домохозяйств и других участников, имеющих возможности для инвестиций, к структурам, которые испытывают недостаток в денежных средствах – компаниям и государствам. Таким образом, «долгие» деньги аккумулируются и находят применение через данный механизм. Финансовый рынок имеет достаточное влияние на благосостояние государств, оказывая помощь сторонам сделок в выборе предмета инвестиций.
Эффективно функционирующий финансовый рынок является необходимой предпосылкой осуществления государственной монетарной политики, а также основой долгосрочной экономической стабильности и роста.
Конкурентоспособные финансовые рынки предоставляют своим участникам доступ к возможностям привлечения денежных средств и управления собственными рисками. Более того, они поддерживают передачу монетарной политики, собирают информацию об участниках и способствуют определению цен на финансовые активы.
Целью данной работы является проанализировать часть модели финансовых рынков на примере ряда развитых стран.
Модель финансового рынка можно представить в следующем виде:
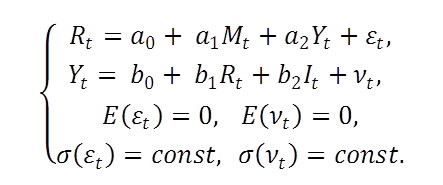
Первое уравнение системы говорит о том, что процентная ставка (
) в экономике зависит от двух показателей: предложение денег (
) на денежном рынке и валовый внутренний продукт (
). Случайная переменная (
) также должна быть включена в уравнение для отражения других факторов, не учитываемых моделью. Мы предполагаем, что ожидание случайной переменной равно нулю, а стандартное отклонение постоянно.
Второе уравнение предполагает, что валовый внутренний продукт () зависит от ставки процента () и инвестиций (
). Как и в первом уравнении системы, мы должны включить случайную переменную.
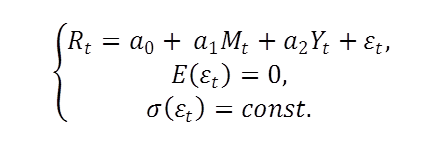Для целей данной работы мы будем использовать первое уравнение системы, которое можно переписать в следующем виде:
В данной модели предложение денег () и валовый внутренний продукт () являются экзогенными или независимыми переменными, ставка процента () является зависимой переменной данной системы.
Для того, чтобы проверить соответствие теоритической модели практическим данным, была собрана информация по пяти развитым странам. В большинстве случаев под «развитой» страной понимается определенный уровень экономического развития, уровня образованности населения, уровень доходов и качество предоставляемых внутри страны услуг со стороны как компаний, так и государства. С целью охватить этот обширный круг вопросов была выбрана классификация стран на основе Индекса развития человеческого потенциала (Human Development Index, HDI). Среди стран, занимающих первые места в данном рейтинге, были выбраны следующие: Австралия, Канада, Сингапур, США, Швейцария.
Была собрана информация по следующим показателям:
• Валовый внутренний продукт
• Ставка процента – реальная процентная ставка
• Предложение денег на денежном рынке – агрегат М3
На основе полученных данных мы построили точечные диаграммы для каждой страны, отражающие зависимость между эндогенной и экзогенными переменными (Диаграмма 1). Для примера мы берем Соединенные Штаты Америки.
Диаграмма 1. Зависимость между реальной ставкой процента и суммой валового внутреннего продукта и широкого показателя денежной массы
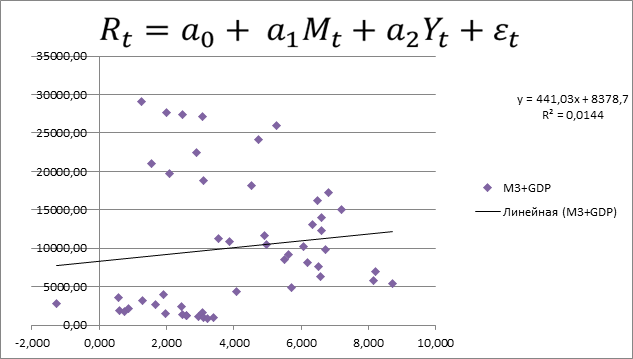
На диаграмме изображена зависимость переменных модели: каждому значению реальной ставки процента соответствует сумма экзогенных переменных, что обозначено точкой на графике. Также добавлены линия тренда, описывающая данную линейную зависимость, и значение достоверности аппроксимации.
Затем с помощью регрессионного анализа модель была оценена, результат выглядит следующим образом:
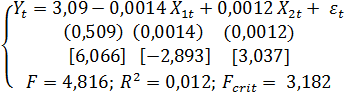
Затем модель была протестирована на соответствие условиям теоремы Гаусса-Маркова и на адекватность, аналогичные процедуры были проведены с данными по другим четырем странам.
Данные всех пяти стран продемонстрировали слабую корреляцию между реальной процентной ставкой и экзогенными переменными при сравнительно высокой корреляции между независимыми переменными. Это говорит о том, что модель не объясняет достаточно большую часть изменений зависимой переменной.
Значение коэффициента достоверности аппроксимации также сравнительно невелико, что позволяет сделать вывод о том, что данная экономическая модель не позволяет оценить большую часть факторов, влияющих на изменение реальной ставки процента.
Согласно F-тесту, который дал положительный результат только в случаев США, четыре модели из пяти имеют низкое качество спецификации. Для этих же четырех стран только один коэффициент является значимым согласно t-тесту, в то время как для США значимыми являются все три коэффициента.
Для трех стран (Канада, Сингапур, США) тест Голдфелда-Квандта пройден, что означает гомоскедастичность остатков модели. Для данных по Австралии и Швейцарии должны быть проделаны дополнительные шаги с целью устранения гетероскедастичности остатков. Среди моделей по пяти странам ни одна не прошла тест Дарбина-Уотса, а значит, во всех моделях присутствует положительная автокорреляция остатков. В этом случае с целью дальнейшего использования должны быть предприняты дополнительные шаги по устранению автокорреляции.
Адекватность всех пяти моделей подтвердилась при помощи построения доверительного интервала, а значит, все пять моделей адекватны по отношению к эмпирическим данным.
Резюмируя все выше сказанное, модель финансовых рынков адекватна по отношению к эмпирическим данным пяти развитых стран, и ее можно использовать для прогнозирования реальной ставки процента. Но также у данной модели имеются ограничения в использовании, поэтому при применении ее на практике следует соблюдать осмотрительность и осторожность.