Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Содержание

Введение. 4

Раздел 1. Состояние вопроса исследования и классификация планетарных передач. 5

1.1 Планетарные передачи, основные понятия. 5

1.2 Обзор ранее выполненных работ. 9

1.3 Исследование повреждений деталей планетарного механизма поворота. 13

1.4 Выводы к первому разделу. 17

Раздел 2. Избыточные связи. 18

2.1 Понятие избыточных связей. 18

2.2 Расчет на избыточные связи применяемых планетарных передач. 23

2.3 Выводы ко второму разделу. 25

Раздел 3. Анализ объекта исследования. 26

3.1 Описание конструкции и работы ПМП Четра-6. 26

3.2 Оценка потенциальных возможностей планетарного механизма поворота Четра-6. 30

3.3 Выводы к третьему разделу. 37

Раздел 4. Предлагаемые конструктивные решения по устранению избыточных связей. 39

4.1 ПП с упругим элементом. 39

4.2 ПП с бочкообразными зубьями. 44

4.3 ПП с карданным шарниром. 49

4.4 Выводы к четвертому разделу. 54

Раздел 5. Предлагаемое изменение в ПМП трактора Четра-6. 56

Заключение. 58

Введение

Одной из ключевых проблем современного тракторостроения является проблема повышения надёжности и долговечности тракторов, что связано с необходимостью снижения затрат на производство продукции.

Решение проблемы повышения надёжности и долговечности тракторов в первую очередь заключается в повышении надёжности и долговечности лимитирующих узлов, к которым относится планетарный механизм поворота (ПМП). Данный тип механизма поворота был внедрён на тракторах в начале 60-х годов взамен бортовых муфт поворота, что позволило снизить металлоёмкость, уменьшить нагруженность коробки перемены передач и главной передачи, повысить срок службы всей трансмиссии.

Механизм поворота является одним из наиболее ответственных узлов тракторов, поскольку выход его из строя связан с потерей управления, причём в большинстве случаев его отказы относят к третьей группе сложности.

Исследования динамики ПМ тракторов показали, что основной причиной преждевременного выхода их из строя является неравномерное распределение нагрузки между сателлитами и по длине зубчатых зацеплений шестерен, вызванное погрешностями изготовления и сборки. При этом чувствительность к погрешностям изготовления и сборки ПМП обусловлена наличием избыточных связей или статической неопределимостью этих механизмов.

По всей видимости, дальнейший рост нагруженности ПМ за счёт увеличения передаваемых мощностей и рабочих скоростей движения приведёт к снижению его долговечности и, как следствие, к повышению себестоимости производимой продукции. Поэтому, проблема повышения долговечности ПМ, носящей отраслевой характер, очевидна, что подтверждает актуальность работ, направленных на её решение.

Раздел 1. Состояние вопроса исследования и классификация планетарных передач.

1.1 Планетарные передачи, основные понятия.

Планетарными называют передачи, имеющие зубчатые колеса с перемещающимися геометрическими осями. Сателлиты обкатываются по центральным колесам, имеющим внешнее или внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Планетарные передачи имеют широкие области назначение и применения:

1. Редуцирование скорости – силовые передачи с малыми удельными габаритами и массой, кинематические передачи с большими передаточными отношениями.

2. Сложение и разложения движения, в том числе с автоматическим управлением скорости в станках, автомобилях и других машинах, многоступенчатые планетарные коробки скоростей, управляемые поочередным торможением звеньев, замкнутые планетарные передачи с встроенной бесступенчатой передачей и т.д.

Преимущества планетарных передач (малые габариты и меньшая масса) объяснятся следующими причинами: а) распределением нагрузки между сателлитами, благодаря чему нагрузки на зубьях меньше в несколько раз; б) большим передаточным отношением в одной ступени, что часто позволяет не прибегать к сложным многоступенчатым передачам; в) широким применением передач с внутренним зацеплением, обладающих повышенной несущей способностью.

Планетарные передачи работают с меньшим шумом, чем простые, что связано с повышенной плавностью внутреннего зацепления, меньшими размерами колес, замыканием сил в механизме и передачей меньших сил на корпус.

Зато планетарные передачи требуют повышенной точности изготовления, имеют, как правило, большее число деталей и сложнее в сборке, чем передачи с неподвижными осями.

Конструкции планетарных рядов достаточно разнообразны. Познакомимся с устройством планетарного ряда на примере наиболее простого и часто используемого (рисунок 1.1). Он состоит из малого центрального колеса (солнца), которое находится в постоянном зацеплении с шестернями, называемыми сателлитами. Сателлиты могут вращаться относительно осей, установленных в водиле. Зубчатое колесо внутреннего зацепления, называемое большим центральным колесом (эпициклом, короной), находится в постоянном зацеплении с сателлитами и окружает всю конструкцию. Следует отметить, что малое центральное колесо, водило и большое центральное колесо вращаются относительно одной общей оси, в то время, как сателлиты планетарной передачи вращаются относительно собственных осей и вместе с водилом относительно общей оси. При этом сателлиты планетарной передачи являются составной частью водила.

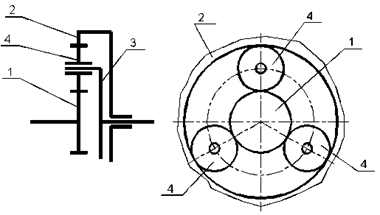
Рисунок 1.1

1 - малое центральное колесо; 2 - большое центральное колесо; 3 - водило; 4 - сателлиты

Название этого механизма происходит от сателлитов, которые подобно планетам, вращаются относительно своих осей и в то же время вокруг малого центрального колеса (солнца).

Основным параметром, определяющим свойства планетарного ряда, является внутреннее передаточное отношение. В общем случае любой планетарный ряд характеризуется шестью внутренними передаточными отношениями. Однако на практике обычно используется только одно, определяемое как отношение частоты вращения малого центрального к частоте вращения большого центрального колеса при остановленном водиле:

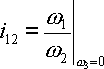. (1.1)

где 1 - индекс малого центрального колеса; 2 - индекс большого центрального колеса; 3 - индекс водила.

В зависимости от того, как вращаются центральные колеса при остановленном водиле, внутреннее передаточное отношение планетарного ряда может быть либо положительным, либо отрицательным. Все планетарные ряды в зависимости от знака внутреннего передаточного отношения, определенного при остановленном водиле, классифицируются на два класса:

1. Планетарные ряды с положительным внутренним передаточным отношением.

2. Планетарные ряды с отрицательным внутренним передаточным отношением.

Надежность - одно из свойств качества продукции. Это свойство изделий проявляется в процессе использования изделий по назначению и рассматривается, как свойство изделия сохранять качество (значения основных эксплуатационных и потребительских характеристик) во времени.

В отечественной практике и в нормативно-технической документации надежность определяется, как свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих спо­собность выполнять требуемые функции в заданных условиях эксплуатации.

Надежность является комплексным свойством и оценивается показателями: безотказностью, долговечностью, ремонтопригодностью и сохраняемостью.

В зависимости от вида изделия его надежность может включать толь­ко часть составных свойств надежности. Так, например, если изделие не подлежит ремонту (подшипник качения и др.) то для таких изделий в свойство надежности не включаются долговечность и ремонтопригодность, для них важно только свойство безотказности, а под­лежащих длительному хранению – еще и свойство сохраняемости.

Безотказность – свойство объекта непрерывно сохранять работоспо­собное состояние в течение некоторого времени или некоторой наработ­ки.

Долговечность – свойство объекта сохранять работоспособное сос­тояние изделия до предельного состояния при установленной системе технического обслуживания и ремонта.

Ремонтопригодность — свойство объекта, заключающееся в приспо­собленности к предупреждению и обнаружению предотказных состоя­ний, отказов и повреждений, поддержанию и восстановлению работоспо­собного состояния путем проведения технического обслуживания и ре­монта.

Сохраняемость — свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение и после хранения и (или) транспортирования.

С позиций надежности различают следующие состояния объекта: исп­равное, неисправное, работоспособное, неработоспособное, предельное. Исправным называется такое состояние объекта, при котором он соответ­ствует всем требованиям нормативно-технической и (или) конструкторс­кой документации. Если имеет место несоответствие хотя бы одному из требований, то такое состояние называется неисправным.

Наработка — это временное понятие, служащее для количественной оценки надежности объекта и характеризует продолжительность или объем работы объекта. Она может измеряться в часах, числах циклов нагружений, километрах пробега и других величинах, определяемых специфи­ческими особенностями изделия.

1.2 Обзор ранее выполненных работ.

Вопросами проектирования планетарных передач, исследованиями их динамики и надёжности в нашей стране и за рубежом в разное время занимались: Э.Л. Айрапетов, К.Б. Арнаудов, Виллис, Э.Б. Вулгаков, А.Е. Гинзбург, Е.Г. Гинзбург, Л.М. Гаркави, Е.Г. Глухарев, Л.В. Григоренко, Б.С. Гахенсон, Е.А. Григорьев, Доббелер, Ю.А.Державец, А.Н. Иванов, К.И. Заблонский, А.Л. Запорожец, В.Ф. Зубков, Г.Ф., Камнев, В.Г. Марков, Ю.Н. Кирдяшев, В.Н. Кудрявцев, Е.С. Кисточкин, И.С. Кузьмин, Н.Г. Кузнецов, В.Р. Каплан, В.С. Колесников, В.Н. Рудницкий, Е.П. Руденко, Н.Ф. Руденко, Д.Н. Решетов, Л.Н. Решетов, Р.А., Свани, Г.И. Скундин, В.С. Сафронов, Р.А Сакаев, И.В. Сигов, Г.И. Татарчук, А.В. Ткаченко, В.М. Труханов, А.Л. Филлипенков, Д.И. Шаткус, Н.А. Щельцын, Шевчук В.П., К.И. Городецкий, В.М. Ястребов, другие учёные и исследователи.

На основании данных исследований были разработаны современные методы проектирования и расчёта планетарных передач, опирающиеся на фундаментальные теоретические основы расчёта и конструирования зубчатых передач с неподвижными осями, в развитие которых большой вклад внесли:

Е. Бэкингем, А.И. Петрусевич, Г. Ниман, И.С. Цитович, В.Д. Андожский, В.А. Белый, Г. Винтер, В.Л. Вейц, М.Д. Генкин, В.А. Гавриленко, Г. Глаубитц, В.К. Гринкевич, Н.А. Ковалёв, Н.И. Колчин, Я.Г. Кистьян, А.Ф. Крайнев, М.Л. Новиков, Б.А. Пронин, Г. Реттиг, С.А. Снесарев, В.Л. Устиненко, Б.А. Тайц, Р.К. Трубин, К.Скрипке, Л.Д. Часовников и другие. По результатам данных исследований в нашей стране был разработан ряд общих и отраслевых методик прочностных расчётов зубчатых передач, которые послужили основой для создания основных нормативных документов.

Сегодня работы в этой области ведутся с целью уточнения использованных приближённых зависимостей; замены применяемых отдельных эмпирических коэффициентов аналитическим учётом влияния всё большего числа факторов; введения в методики вероятностного представления о значениях отдельных параметров, имеющих случайный характер; разработки методик расчёта с новыми видами зацеплений или принципиально новыми конструктивными решениями.

При рассмотрении различных методик прочностных расчётов становиться ясно, что особое внимание в них уделяется точностным характеристикам передачи при определении значений коэффициентов динамической нагрузки и коэффициентов неравномерности распределения нагрузки по длине контактных линий и между сателлитами. При этом расчётные формулы для данных коэффициентов в различных методиках имеют существенные отличия. Следует отметить, что при расчётах планетарных передач используются те же методы, что и для обычных передач с неподвижными осями зубчатых колёс без учёта специфики работы зацеплений в планетарном ряду. Однако, многими исследователями отмечается тот факт, что при проектировании планетарных передач требования к их точности должны быть более высокими, чем у обычных зубчатых передач.

Вопросам исследования планетарных передач посвящено большое количество работ исследователей: К.Б. Арнаудова, Г.Г. Баранова, Н.Г. Бруевича, В.А. Добровольского, А.Л. Запорожца, Ю.З. Кирия, Н.Й. Колчина, М.А. Крейнеса, Ф.Э. Кравчука, А.А. Кроль, В.Н. Кудрявцева, А.А. Никитина, Л.Н. Решетова, Н.Ф. Руденко, М.Л. Скрипки, Л.П. Смирнова, А.Г. Шолухи, Л.Б. Эльштейна и других авторов.

Среди зарубежных исследователей планетарных передач наиболее известны Бранденбергер, Виллис, Доббелер, Свани, Штраух и другие.

Работы, посвященные планетарным механизмам, продолжают публиковаться и сейчас, что объясняется большой заинтересованностью промышленности в их широком применении и стремлением к накоплению экспериментальных и теоретических материалов для усовершенствования методики проектирования.

Работа М.А. Скрипки посвящена экспериментальному определению неравномерности распределения нагрузки по сателлитам в планетарных передачах при различных числах сателлитов на установившихся и переходных режимах работы. Исследования проведены с передачей, имеющей уравнительный механизм и без него. Эксперименты проведены на установке, работающей по замкнутому контуру с трех-, четырех-, и пятисателлитными планетарными передачами. Уравнительный механизм представлял собой шлицевую эвольвентную муфту. Нагруженность сателлитов определялась методом регистрации изгибных деформаций осей сателлитов. В результате экспериментальных исследований получены зависимости коэффициентов неравномерности распределения нагрузки между сателлитами от величины внешней нагрузки и скорости вращения, количества сателлитов и наличия уравнительного механизма. Определено, что увеличение количества сателлитов приводит к заметному увеличению коэффициента неравномерности. Для трехсателлитной передачи без уравнительного механизма

,

а с уравнительным механизмом

. Автором получен вывод о снижении коэффициента неравномерности распределения нагрузки между сателлитами с увеличением передаваемого крутящего момента. На основании просмотра осциллограмм высказано утверждение, что функции усилий, действующих на сателлиты, являются периодическими функциями с периодом, равным кинематическому периоду передачи. Главными названы первые гармоники, отнесенные к одному обороту каждой шестерни.

Практике доводки планетарного редуктора трансмиссии самоходного комбайна СК-4 посвящена публикация Д.И. Шаткуса. По ходу экспериментальных исследований, проводимых при работе механизма с нагрузкой 0, 300 и 600 кгм., выяснилось, что для устранения имевших место поломок необходимо перейти от статически неопределимой к статически определимой системе. Применение «плавающей» солнечной шестерни позволяет сократить число избыточных связей с восьми до шести. Наличие дорого «плавающего» звена позволяет сократить число избыточных связей до двух. Установка в названном редукторе «плавающей» шестерни и сателлитов на сферических опорах с роликовыми подшипниками позволила значительно, в 3-4 раза, увеличить о работоспособность.

Экспериментальному исследованию влияния материала, твердости и точности зубчатых колес, величины нагрузки и скорости вращения, количества сателлитов планетарных редукторов на распределение нагрузки между сателлитами посвящена работа Н.Е. Перевалова.

Вопросам исследования равномерности распределения нагрузки в зацеплениях зубьев простых передач посвящено значительное количество теоретических и экспериментальных работ советских и зарубежных авторов. Среди них: работы Б.Н. Акуленко, П.Ф. Балюнова, И.И. Беспальцева, А.Г. Гашинского, М.Д. Генкина, В.Ф. Головкина, В.К. Гринкевича, Я.Г. Кистьяна, А.К. Климова, В.Н. Кудрявцева, А.И. Петрусевича, М.С. Полоцкого, Д.Н. Решетова, А.А. Фролова, Л.Д. Часовникова, Е.А. Чудакова, Х. Меррита, Г. Тевена и других.

Впервые задача о неравномерности распределения нагрузки в зацеплении была рассмотрена А.И. Петрусевичем в 1938-1939 годах. В последующих работах названных выше авторов были развиты и уточнены многие положения, уточняющие и дополняющие выявленные закономерности.

Л.М. Гаркави рассматривает распределение нагрузки по ширине венцов шестерен планетарных редукторов, считая, что они нагружаются только крутящим моментом.

В работе ряда авторов, показано, что закон распределения нагрузки по длине контактной линии прямозубой цилиндрической передачи, с достаточной для инженерных расчетов точностью, можно считать линейным. Из этого предположения исходили при анализе работы планетарных передач и авторы некоторых названных выше работ.

1.3 Исследование повреждений деталей планетарного механизма поворота

Виды повреждений деталей трактора делят на две группы: допустимые, и недопустимые. При этом разрушению или деформации может подвергаться как тело детали, так и ее поверхность, находящаяся во взаимодействии с поверхностью сопряженной детали. Разделение повреждений на допустимые и недопустимые зависит не только от характера повреждений, но и от требований, предъявляемых к данному узлу или детали трактора. Виды и величины повреждений определяют содержание ремонтов машины.

Основным видом повреждения деталей тракторов являются допустимые повреждения, вызванные в основном старением материалов деталей, при этом повреждения элементов машины могут привести к ее отказам, если степень повреждения превзошла допустимый уровень. Под процессом старения материала здесь понимаются необратимые изменения свойств или состояния материала детали в результате действия различных факторов.

Согласно А.С. Проникову, классифицировать необратимые процессы старения следует по области детали, в которой проявляется данный процесс, и в зависимости от того внешнего проявления, к которому привел данный процесс (см. таблицу 1.1). По внешнему проявлению, т.е. по деформации детали, ее износу, изменению свойств и другим показателям, можно судить о степени повреждения детали и, следовательно, оценить близость детали к ее предельному состоянию.

Наиболее часто процессы старения протекают в поверхностных слоях. При этом поверхность детали может подвергаться температурным, химическим, механическим или иным воздействиям внешней среды. В результате чего могут происходить процессы, связанные с потерей материала или, наоборот, с присоединением материала. В результате внешних воздействий возможно также изменение свойств поверхностного слоя. При контакте двух сопряженных поверхностей протекают разнообразные процессы износа, приводящие к изменению условий контакта, что влечет, как правило, к изменению параметров сопряжения.

Таблица 1.1 - Классификация процессов старения по А.С. Проникову (необратимые процессы)

Следует отметить, что все обозначенные процессы могут протекать одно­временно в различных сочетаниях. При этом какие-то разновидности процес­сов преобладают, а какие-то сопровождают процесс старения машины.

Для шасси тракторов характерны все виды повреждений, указанные в таблице 1.1, однако доля каждого вида повреждения в процессе достижения машиной предельного состояния различна. Установлено, что при совре­менном уровне техники 85..90% машин выходят из строя в результате изнаши­вания и только 10..15% по другим причинам, в основном по причине недоста­точной усталостной прочности деталей, что связано со спецификой работы сельхозмашин в абразивных средах.

При оценке уровня износостойкости деталей шасси тракторов в условиях рядовой эксплуатации проводилась дефектовка деталей, лимитирующих ресурс трактора. Результаты данной дефектовки показывают, что детали ПМП данных тракторов выходят из строя в результате изнашивания. При этом характер износа бывает нескольких видов и зависит от разновидности процесса изнашивания.

Классификации видов изнашивания базируются на выделении основных факторов, определяющих тот или иной процесс изнашивания. По ГОСТ 16429 все виды изнашивания делятся на три основные группы (рисунок 1.2).

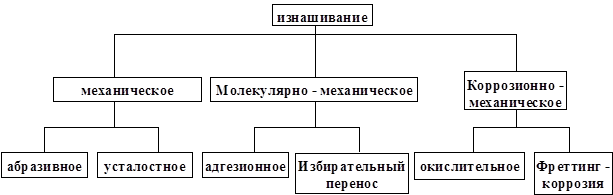
Рисунок 1.2 - Классификация видов изнашивания

Механическое изнашивание происходит в результате только механических взаимодействий материалов изделия; молекулярно-механическое сопровождается также воздействием молекулярных или атомарных сил; корозионно - механическое изнашивание происходит при трении материала, вступившего в химическое взаимодействие со средой.

Согласно современным представлениям о ходе процесса изнашивания типичным видом его протекания во времени является процесс, имеющий три характерные стадии: 1 - приработка, 2 - установившийся износ, 3 - ускоренный (катастрофический) износ (см. рисунок 1.3).

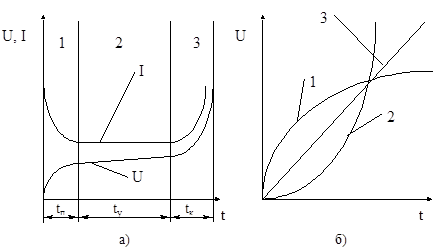
Рисунок. 1.3 - Изменение износа и интенсивности изнашивания во времени

а) – характерные стадии износа; б) – встречающиеся виды процессов износа

В период приработки 1 происходит изменение макро- и микрогеометрии поверхности, устанавливается равновесная шероховатость, уменьшается сила трения и температура контакта. Из-за увеличения фактической площади контакта, снижаются контактные давления, происходят структурные, физические, химические и механические изменения поверхностных слоев.

При установившемся 2 процессе изнашивания стабилизируются сила трения, температура и скорость изнашивания.

Период ускоренного (катастрофического) износа вызывается различными причинами: изменением геометрических характеристик сопряжения, повышением динамических нагрузок, температур контакта, истиранием защитных износостойких слоев и т.п. Интенсивность изнашивания I имеет соответственно три характерных периода.

В некоторых случаях процесс изнашивания может протекать несколько по-другому (рисунок 1.3.б). Хотя на рисунке 1.3.б не показаны характерные периоды процесса изнашивания, они могут присутствовать в более или менее выраженной форме.

Специфика работы ПМП накладывает свои особенности на характер износа деталей сопряжений.

1.4 Выводы к первому разделу

Действительные значения ресурса планетарного механизма поворота тракторов Четра не превышают 10тыс моточасов, что в два раза ниже современных требований к ресурсу тракторов. Дальнейшее увеличение нагруженности механизма приведёт к снижению его долговечности.

Требования к надежности, наработке на отказ по первой группе сложности, к трансмиссии тракторов за 2005-2010гг возрастает с 7000..8000 моточасов до 13000..15000 моточасов в зависимости от тягового класса.

В разделе приведены сведения о планетарных механизмах, их преимуществах и недостатках. Дан анализ работ, ранее выполненных исследователями, по уменьшению неравномерности распределения нагрузки между сателлитами и по длине контактных линий, по повышению нагрузочной способности планетарных передач. Приведены данные по исследованию разрушения планетарных передач тракторов. Дана классификация планетарных передач по конструктивным способам устранения избыточных связей.

Раздел 2. Избыточные связи.

2.1 Понятие избыточных связей.

Статически определимые механизмы известны давно, но до сих пор, ни в одном курсе по теории механизмов и машин не отражены их достоинства. Такие механизмы позволяют расширить допуски на изготовление, уменьшить трудоемкость, удеше­вить производство и повысить надежность машин. В отдельных случаях упроща­ется конструкция механизмов и увеличивается их прочность. Работа статически определимых механизмов не нарушается при изменении размеров звеньев. Они обладают повышенной нагрузочной способностью и малым трением.

Размеры звеньев могут изменяться и во время эксплуатации вследствие про­садки фундамента, износа и регулировки зазора кинематических пар, упругих деформаций, (например, прогибов валов), расширения от нагрева, а также ошибки при ремонте и сборке (например, если перепутали вкладыши подшипников). На статически определимый механизм изменение размеров звеньев не влияет. Следо­вательно, статически определимые механизмы дают не только снижение трудоем­кости, но и одновременно повышают надежность.

Избыточные связи в механизме вредны, так как они увеличивают трудоемкость изготовления и эксплуатации механизмов и снижают их надежность.

Поэтому важно выбирать схему механизма так, чтобы требования к точности звеньев были невелики. Этому удовлетворяют механизмы, статически определи­мые, т. е. без избыточных (пассивных) связей, звенья которых самоустанавливаются.

Избыточными (пассивными) связями называются такие связи, устранение которых не увеличивает подвижности механизма.

Избыточные связи в механизме вредны, так как они увеличивают трудоемкость изготовления и эксплуатации механизмов и снижают их надежность.

Число избыточных связей для многих механизмов равно числу размеров, требующих точного выполнения. Иногда это число значительно больше числа избыточных связей. Поэтому важно наличие избыточных связей в механизме, а не их количество.

Может быть общая и местная (пассивная) подвижность механизма. Местной условимся называть такую, которая не влияет на подвижность механизма в целом. Местную подвижность имеют ролики (вследствие возможного проскальзывания), блоки, шкивы, плавающие втулки и пальцы, шатуны и цилиндрические ползуны с шаровыми головками, а также кольца подшипников качения, если они на подвижной посадке (при рассмотрении подшипника).

Для вывода структурной формулы воспользуемся классами кинематических пар, т. е. числом связей, обусловленных данной парой. Связями в кинематической паре называют ограниченные относительные перемещения по заданной оси координат и ограниченные угловые перемещения вокруг этой оси.

Если число подвижных звеньев равно п, то они имеют 6n степеней свободы (каждое звено — три перемещения по трем осям координат и три вращения). Для определения подвижности механизма из них надо вычесть связи, накладываемые кинематическими парами.

Число Pi кинематических пар i-го класса накладывает ipi условий связи, а все кинематические пары условий связи. Однако вычитать следует не все связи, так как избыточные связи (их число обозначим через q) дублируют другие связи, не уменьшая подвижности механизма, а только обращая его в статически неопределимую систему. Поэтому подвижность механизма 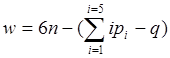. Эта формула (в несколько ином виде) предложена А. П. Малышевым 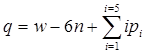. (2.1)

Отсюда или в развернутом виде

. (2.2)

Формулу А. П. Малышева можно также вывести из выражений для определения как внешних, так и внутренних (в кинематических парах) нагрузок в механизме.

В статически определимом механизме уравнений равновесия звеньев хватает для определения этих нагрузок. В механизме с избыточными связями их приходится дополнять уравнениями деформаций. Количество таких уравнений и будет равно числу избыточных связей.

Число внешних нагрузок — сил или моментов равно w+1, что легко проверить на механизмах с w = 1, 2 и т. д.

Одна нагрузка всегда задана, поэтому число неизвестных внешних нагрузок равно w. Каждая кинематическая пара г-го класса передает i нагрузок (сил и моментов); которые и будут неизвестными, а у всех пар будет неизвестных.

Всего в механизме неизвестных, уравнений равновесия п звеньев будет 6n.

Недостающих уравнений, которые восполняются уравнениями деформаций, , т. е. та же формула Малышева.

У звена с местной подвижностью момент внешних сил вокруг соответствующей оси должен быть равен нулю. Это равенство может служить для контроля вычислений.

Рассмотрим некоторые кинематические пары (Рисунок 2.1). Классы обозначены римскими цифрами I, II, III’, III”, IV и V, столбцы — арабскими цифрами 1 - 5.

Каждую пару обозначим римской цифрой с индексом, соответствующим номеру столбца рисунка 2.1. Такое обозначение позволяет легко найти по рисунку 2.1 кинематическую пару, примененную в рассматриваемой схеме механизма.

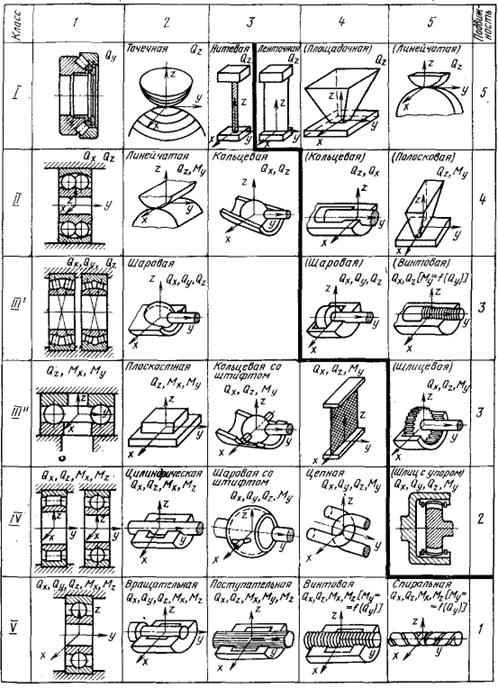
Рисунок 2.1 - Классы кинематических пар

Для каждой пары даны силы и моменты, передаваемые ею. По этой таблице можно найти подвижность кинематической пары, т. е. число движений линейных и угловых, которые она оставляет между звеньями. Вообще сумма класса пары и подвижности всегда равна шести.

Для получения пары любого класса пары следует соединять параллельно. При этом сумма классов соединяемых пар равна классу получаемой пары, а при наличии избыточных связей эта сумма равна классу получаемой пары плюс число избыточных связей.

При решении вопроса о том, какие избыточные связи следует оставить, когда не удается устранить их полностью, можно пользоваться и плоской схемой. Для этого можно рассматривать проекцию всех звеньев на одну плоскость или совмещать все звенья с одной плоскостью.

На плоской схеме нельзя обнаружить силы, действующие по оси z с соответствующими избыточными связями, и моменты вокруг осей х и у также с соответствующими избыточными связями, которые бывают у плоских механизмов. На этой схеме можно исследовать только силы по осям х и у, моменты вокруг оси z и соответствующие им избыточные связи, которые обозначим через qn.

Вообще плоская схема не может полностью отразить работу механизма так же, как одна проекция не может полностью его изобразить. Подвижность wп механизма на плоской схеме отличается от действительной подвижности w, так как плоская схема не учитывает вращения звеньев вокруг осей, расположенных в плоскости хоу.

Выведем формулу для плоской схемы. Любое подвижное звено на плоскости имеет три степени свободы, а всего 3n степеней свободы.

Каждая вращательная пара независимо от того, является ли она парой пятого, четвертого, третьего или даже второго класса (кольцевая), на плоской схеме накладывает два условия связи — ограничивает перемещения по осям х и у. Каждая поступательная пара независимо от того, является ли она парой пятого, четвертого или третьего класса, накладывает на плоской схеме два условия связи — ограничивает перемещение в направлении, перпендикулярном к перемещению в этой паре, и ограничивает вращение вокруг оси, перпендикулярной к плоскости механизма. Следовательно, на плоской схеме низшие пары накладывают 2рн условий связи.

2.2 Расчет на избыточные связи применяемых планетарных передач

Планетарные передачи в многосателлитном исполнении выгодно отличаются от передач с неподвижными осями меньшими габаритами и массой. Например, при одинаковых передаваемых моментах и поперечных габаритах (когда сумма диаметров колес одноступенчатой зубчатой передачи равна диаметру опорного колеса однорядной планетарной), при трех сателлитах и передаточных числах и = 3÷7 окружные усилия в планетарной передаче в 6 — 4 раза меньше, чем в простой передаче

В однорядном планетарном механизме без плавающего звена с тремя сателлитами и подшипниками пятого класса (Рисунок 2.3) имеется восемь избыточных связей при 3-х сателлитах. Большое число избыточных связей требует очень точного исполнения таких механизмов, иначе они очень плохо работают. Так же эта схема применялась на тракторе ДТ-75.

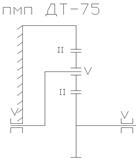
Рисунок 2.3 - Обычный ПМ

. (2.2)

Как видно с увеличением числа сателлитов число избыточных связей возрастает. При этом так же возрастает и число связей влияющих на распределение нагрузки между сателлитами с 2-х до 4-х. Так же с увеличением числа сателлитов уменьшается и оценка механизма ОИС – с 0,52 до 0,48.

Неравномерное распределение нагрузки между сателлитами легко устраняется применением плавающего звена. Неравномерное распределение нагрузки по длине зуба устраняется дополнительными угловыми подвижностями. Их лучше всего получить постановкой сателлитов на сферические пары III (Рисунок 2.4).

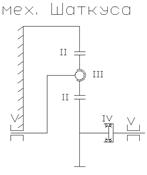
Рисунок 2.4 - Механизм Шаткуса

(2.3)

К сожалению, при малых передаточных числах (малый диаметр сателлита) в нем не умещается сферический подшипник достаточной работоспособности. Область применения этой схемы можно значительно расширить, если в качестве наружного кольца сферического подшипника использовать сам сателлит, прошлифовав в нем внутреннюю сферу («сателлит — подшипник» предложил Г. А. Снесарев). Правда, это потребует разработки ГОСТа на такие сателлиты и организации специализированного производства.

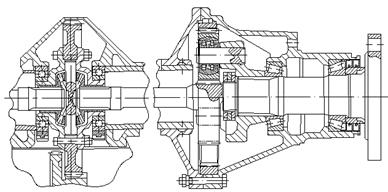
Рисунок 2.5 - Редуктор Шаткуса для зернового комбайна.

По расчетам видно из расчета, что механизм Шаткуса не имеет избыточных связей в 3-х сателлитом исполнении, при 4-х имеется 1 избыточная связь, при 5-ти сателлитах 2 избыточные связи. Недостатком так же является то, что данная передача не обладает возможностью самоустановки водила с сателлитами под воздействием радиальных и тангенциальных сил, возникающих в зацеплениях сателлитов с центральными колесами, что снижает ее надежность и долговечность.

2.3 Выводы ко второму разделу.

В разделе были даны понятия избыточных связей в механизмах, показано влияние их на работоспособность планетарных передач, методы проверки на избыточные связи с учётом классов кинематических пар. Приведена программа экспертной оценки избыточных связей и эмпирическая формула их количественной оценки. Так же были посчитаны различные планетарные передачи и механизмы на избыточные связи. Наименьшее количество избыточных связей было получено в ПП2 Браслет и механизме Шаткуса, даже не смотря на их недостатки они являются удачными техническими решения, которые позволяют повысить надежность и ресурс планетарных узлов тракторов. Именно эти технические решения позволяют опираться при разработке новых технических решений.

Раздел 3. Анализ объекта исследования.

3.1 Описание конструкции и работы ПМП Четра-6.

Конструкция исследуемого однопоточного однорядного одноступенчатого планетарного механизма поворота, выполненного по схеме 2H-K представлена на рисунке 3.1.

Планетарный механизм поворота состоит из центрального колеса внутреннего зацепления 5 (коронная шестерня), центрального колеса внешнего зацепления 7 (солнечные шестерни), сателлитов 4, осей сателлитов 3, водила 2, вала 1, барабана 6, шестерни 8 управляемой гидромотором.

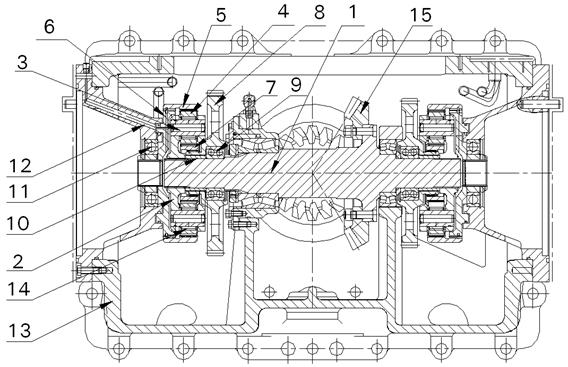
Рисунок 3.1 - Планетарный механизм поворота Четра-6

Центральное колесо внешнего зацепления 7 установлено на управляемое гидромотором шестерни 8, посредством шлицевого соединения с упором, установленной на двухрядном радиальном шариковом подшипнике 9. Также установлена на втулку 10 с зазором, установленную на валу 1 и прижимается водилом 2. Центральное колесо внутреннего зацепления 5 установлено на барабане 6, посредствам шлицевого соединения с упором. Барабан 6 установлен на однорядный радиальный шариковый подшипник 11, установленный в стакан 12 прикрепленному к корпусу главной передачи 13.

Сателлиты 4 устанавливаются на осях 3 посредством игольчатых подшипников 14 и находятся в постоянном зацеплении с центральными колёсами. Оси 3 крепятся в расточках щёк водил 2. Водила 2 соединяются с одним из концов валов 1, на котором установлена ведущая шестерня 15 конечной передачи. Соединение вала 1 с водилами 2 осуществляется посредством шлицевых соединений.

Основные конструктивные параметры шестерен ПМП представлены в таблице 3.1.

Таблица 3.1 Конструктивные параметры шестерен ПМП Четра-6.

ПМП Четра 6 работает при прямолинейном движении следующим образом с вала заднего моста 1, момент передается на водило 2, в котором на осях 3 установлены четыре сателлита 4. Сателлиты 4 обкатывают солнечную шестерню 7, установленную на шестерни 8, остановленной гидромотором и передают момент на коронную шестерню 5, установленной на барабан 6, который передает момент на конечную передачу. В данном механизме плавающими являются солнечная и коронная шестерни, имеющие шлицевое соединение с упором рис. 3.1, 3.4.

Также работу ПМП отображает кинематическая схема трактора представленная на рис. 3.2, 3.3.

В режиме прямолинейного движения обе управляемые шестерни 8, остановлены гидромотором ПМП. Солнечные шестерни 7, установленные на шестерни 8, остановлены. Крутящий момент от водила 2 передаётся каждому из сателлитов 4, через зацепления с центральными колёсами 7, момент передаётся коронной шестерни 5 и далее через барабан 6 на валы конечных передач.

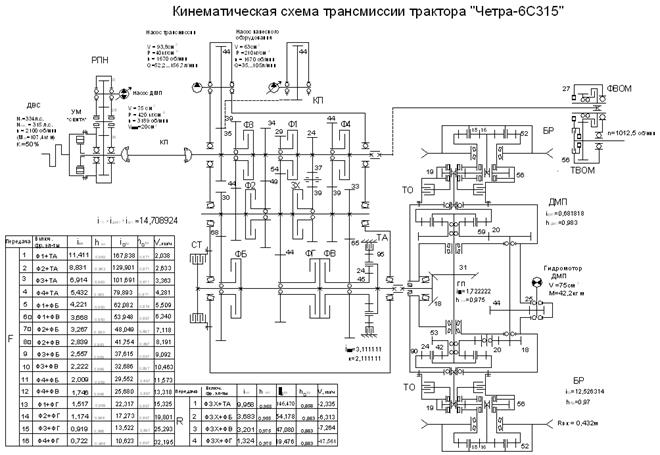
Рисунок 3.2 кинематическая схема трансмиссии Четра-6

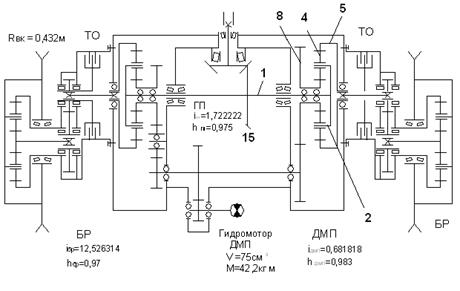
Рисунок 3.3 кинематическая схема ДМП и БР Четра-6

Величина крутящего момента, передаваемого каждым планетарным рядом на данном режиме, будет равна половине крутящего момента, подводимого к шестерне 15 главной передачи и будет лимитироваться тяговосцепными свойствами движителя.

В режиме плавного поворота включается гидромотор ДМП, приводя в движение управляемые шестерни 8. Причем за счет использования промежуточной паразитной шестерни, управляемые шестерни 8, вращаются в разные стороны, приводя в движение солнечные шестерни 7. Таким образом получается что часть момента забирается с одного борта и передаётся на другой. Оба остановочных тормоза отпущены. За счет разницы моментов на планетарных рядах происходит плавный поворот.

В режиме крутого поворота полностью затормаживают один из остановочных тормозов в зависимости от направления поворота. При этом основная часть крутящего момента будет передаваться через второй планетарный ряд и ограничиваться тяговосцепными свойствами движителя. Что происходит за счет работы гидромотора и дифференциального механизма. Другой планетарный ряд нагружается моментом равным по величине моменту сопротивления проворачиванию солнечной шестерни. В этом режиме обеспечивается минимальный фиксированный радиус поворота.

3.2 Оценка потенциальных возможностей планетарного механизма поворота

Согласно расчётам ПМП трактора Четра-6 по критерию статической прочности при действии максимальной нагрузки детали планетарного ряда имеют значительный запас, поэтому оценку потенциальных возможностей механизма будем вести по критериям контактной и изгибной усталостной прочности зубьев шестерен планетарного ряда, а также по критерию долговечности игольчатого подшипника сателлита и опор коронной шестерни (п/ш 226). На долговечность опор коронной шестерни (п/ш 226) режимы работы механизма влияния не оказывают, поскольку равнодействующая радиальных сил действующих в зацеплениях планетарного ряда практически равна нулю, поэтому для оценки потенциальных возможностей по критериям долговечности игольчатого подшипника и п/ш 226 воспользуемся соответственно гистограммами. Долговечность подшипников определим по известной формуле:

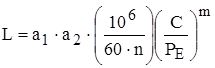, (3.1)

где С – динамическая грузоподъёмность подшипника, Н; РЕ – эквивалентная нагрузка на подшипник, Н; n – частота вращения подшипника, об/мин; m=3 для шариковых подшипников и m=10/3 для роликовых подшипников; а1 – коэффициент надёжности; а2 – обобщающий коэффициент совместного влияния качества металла и условий эксплуатации.

Для оценки потенциальных возможностей механизма по критериям контактной и изгибной усталостной прочности зубьев шестерен планетарного ряда воспользуемся гипотезой Пальмгрена-Майнера о линейном характере накопления усталостных повреждений [4]:

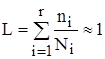, (3.2)

где L – мера повреждения материала; ni – число циклов нагружения с амплитудой напряжения i-го уровня; Ni - число циклов нагружения с амплитудой напряжения i-го уровня, при непрерывном действии которого материал разрушается; r - количество уровней напряжения за весь период работы.

С другой стороны усталостную прочность можно характеризовать известной кривой усталости Велера, описываемой уравнением

, (3.3)

где si – напряжение i-го уровня; Ni – число циклов нагружения, соответствующее напряжению i-го уровня; m – показатель степени; А – постоянная.

Данное уравнение описывает кривую Велера при напряжениях si>slim, где slim – предел выносливости материала при характерном виде цикла нагружения, при этом для любого уровня справедливо соотношение

, (3.3)

где NG – базовое число циклов нагружения, соответствующее пределу выносливости slim.

Подставляя (3.4) в (3.2) получим

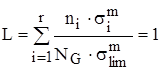(3.5)

Число циклов нагружения ni для зуба сателлита, солнечной и коронной шестерни определиться по следующим выражениям:

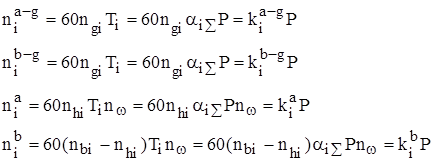(3.6)

где aiå – суммарный коэффициент использования рабочего времени (aiå=ai×br); Р – заданный ресурс; – частоты вращения сателлита, водила, и коронной шестерни соответственно; , - число циклов нагружения сателлита в зацеплениях a-g и b-g соответственно; , - число циклов нагружения коронной и солнечной шестерни соответственно.

Подставляя (3.12) в (3.11) после преобразований получим выражение для определения ресурса детали по рассматриваемому критерию:

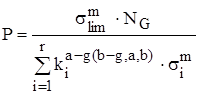(3.7)

Для определения ресурса по указанным критериям и оценке потенциальных возможностей необходимо привести гистограммы распределения крутящих моментов к эквивалентным гистограммам распределения контактных и изгибных напряжений в зубьях шестерен.

Величины контактных sН и изгибных sF напряжений будем определять по общепринятым в машиностроении формулам:

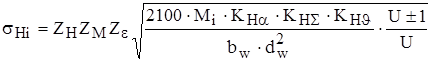, (3.8)

где ZH – коэффициент, учитывающий форму сопряжённых поверхностей в полюсе зацепления; ZM – коэффициент, учитывающий механические свойства материалов сопряжённых зубчатых колёс, ; Ze - коэффициент, учитывающий суммарную длину контактных линий; U – передаточное число; bw – длина зацепления, мм; dw – начальный диаметр шестерни, мм; Мi – крутящий момент на шестерне, Н×мм; KHa - коэффициент, учитывающий распределение нагрузки между зубьями; КHS – обобщённый коэффициент неравномерности, учитывающий распределение нагрузки по длине зацепления с учётом распределения нагрузки между сателлитами; KHu - коэффициент, учитывающий динамическую нагрузку в зацеплении.

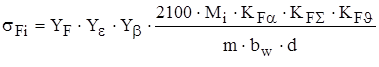, (3.9)

где YF – коэффициент, учитывающий форму зуба; Ye - коэффициент, учитывающий перекрытие зубьев, Yb - коэффициент, учитывающий наклон зуба; KFa - коэффициент, учитывающий распределение нагрузки между зубьями при расчёте зубьев на выносливость при изгибе; КFS - обобщённый коэффициент неравномерности, учитывающий распределение нагрузки по длине зацепления с учётом распределения нагрузки между сателлитами при расчёте зубьев на выносливость при изгибе; KFu - коэффициент, учитывающий динамическую нагрузку в зацеплении при расчёте зубьев на выносливость при изгибе; m – модуль зубьев; d – диаметр начальной окружности.

В выражениях (3.8) и (3.9) обобщённые коэффициенты неравномерности, учитывающие распределение нагрузки по длине зацепления и между сателлитами определяются по формулам:

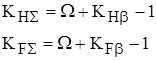, (3.10)

где W - коэффициент неравномерности распределения нагрузки между сателлитами; KHb, KFb - коэффициенты, учитывающий распределение нагрузки по длине зубьев соответственно для контактных и изгибных напряжений.

Из результатов расчёта видно, что на всех режимах работы ПМП, возникающие контактные и изгибные напряжения трактора Четра-6 не превышают значений соответствующих пределов выносливости sHlim, sHlimгл,sFlim, а также величин допускаемых контактных sHPmax и изгибных sFPM напряжений (критерий статической прочности). Следовательно, по рассматриваемым критериям, при данной нагруженности, механизм может работать бесконечно долго, что свидетельствует о его значительных потенциальных возможностях.

При проведении расчёта было принято, что обобщённый коэффициент неравномерности распределения нагрузки по длине контактных линий и между сателлитов W=KHå(KFå)=1 (поскольку KHå»KFå, то обозначим KHå=KFå= Kå). Однако на самом деле данные коэффициенты никогда не равны единице ввиду неизбежности получения погрешностей при формировании деталей и сборке любого узла, а также по причине наличия деформаций элементов планетарного ряда при нагружении. Поэтому при расчётах очень важно правильно оценить данные параметры, поскольку от этого в значительной степени зависит долговечность проектируемого узла.

Значение коэффициента неравномерности распределения нагрузки между сателлитами W может находиться в пределах от 1 до 3, а значение коэффициента неравномерности распределения нагрузки по длине контактных линий KHb(KFb) от 1 до 2, поскольку зависимости (3.8), (3.9) остаются справедливыми при значениях KHb(KFb)£2 (на практике KHb(KFb) может иметь значения ³2). Таким образом, суммарный коэффициент неравномерности распределения нагрузки, при условии, что KHb(KFb)£2 может иметь значения от 1 до 4.

Подставляя в выражения (3.8), (3.9) исходные данные, получим следующие зависимости для определения контактных и изгибных напряжений исследуемого механизма:

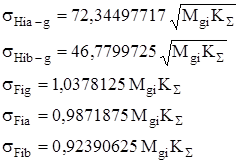(3.11)

Используя выражения (3.5), (3.6), (3.11) произведём расчёты и построим зависимости долговечности от величины Kå по контактным, глубинным напряжениям и напряжениям изгиба для каждой шестерни планетарного ряда (рисунок 3.4).

Из графиков видно, что с увеличением Kå, начиная со значений при которых действующие напряжения оказываются выше предела выносливости, происходит резкое падение долговечности по всем критериям. При этом лимитирующими элементами по этому критерию оказываются коронная шестерня и сателлит, которые, согласно графику выйдут из строя раньше других, если величина Kå будет ³2,2.

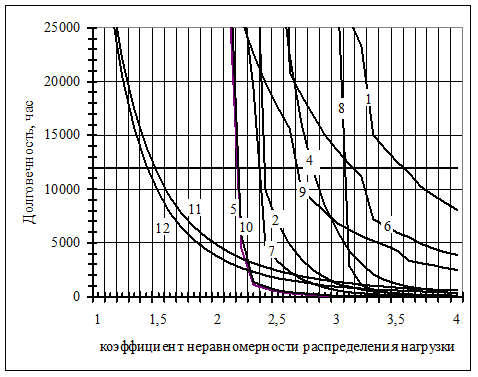
Рисунок 3.4 – Графики изменения долговечности ПМП по различным критериям

Долговечность: 1 - сателлита по контактным напряжениям в зацеплении; 2 - сателлита по глубинным контактным напряжениям в зацеплении; 3 - сателлита по контактным напряжениям в зацеплении; 4 - сателлита по глубинным контактным напряжениям в зацеплении; 5 - сателлита по напряжениям изгиба; 6 - солнечной шестерни по контактным напряжениям; 7 - солнечной шестерни по глубинным контактным напряжениям; 8 - солнечной шестерни по напряжениям изгиба; 9 - коронной шестерни по контактным напряжениям; 10 - коронной шестерни по напряжениям изгиба; 11 - подшипника коронной шестерни; 12 - подшипника сателлита.

Линия 3 на рисунке 3.4 находится вне области построения, ввиду значительного запаса прочности по данному критерию.

Для определения потенциальных возможностей повышения нагруженности механизма вместо коэффициента Kå в формуле (3.11), введём величину приведенного коэффициента неравномерности распределения нагрузки

Kåобщ= Kå× KåF (3.12)

где KåF – коэффициент увеличения нагрузки.

Также вместо величины эквивалентной нагрузки PEi в формуле (3.12) введём произведение PEi×Kåп/ш, где Kåп/ш=W× KåF для подшипника сателлита и Kåп/ш=KåF для подшипника коронной шестерни, а графики, изображённые на рисунке 3.8 дополним зависимостями долговечности подшипников сателлитов и коронной шестерни от величины Kåп/ш, из которых видно, что долговечности в 12000 часов соответствует коэффициент Kåп/ш=1,4. Это означает, что для обеспечения данной долговечности коэффициент W не должен превышать величины равной 1,4, следовательно, при обеспечении в механизме равномерного распределения нагрузки между сателлитов имеется возможность увеличить нагрузку передаваемую через планетарный ряд в 1,4 раза при сохранении режимов нагружения.

В кандидатской диссертации В.П. Шевчука экспериментальным путём было получено значение коэффициента неравномерности распределения нагрузки между сателлитами W=1,54 (Р=8872 часа), следовательно, по критерию долговечности опор сателлитов необходимая долговечность ПМП не обеспечивается, что требует разработки технических решений, позволяющих снизить значение W.

Таким образом, установив предельное значение коэффициентов [Kåобщ] и [Kåп/ш], можно определить возможные границы повышения нагруженности любой зубчатой передачи по рассмотренным выше критериям при заданных значениях коэффициентов KHb(KFb) и W.

Исходя из проведённого выше исследования и основываясь на полученных зависимостях (см. рисунок 3.4) можно заключить, что у исследуемого механизма имеются потенциальные возможности для обеспечения требований к ресурсу и повышения его нагруженности. Элементами, которые ограничивают возможность повышения нагруженности при условии обеспечения равномерного распределения нагрузки по длине контактных линий и между сателлитами, являются подшипники сателлитов и коронной шестерни.

Таким образом, величина приведённого коэффициента неравномерности распределения нагрузки является мерой оценки потенциальных возможностей зубчатой передачи. Поэтому для повышения долговечности исследуемого механизма необходимо повысить значение данного параметра за счёт создания наиболее благоприятных режимов работы, улучшения свойств материала (повышение пределов выносливости), улучшения геометрии зацепления и др.

3.3 Выводы к третьему разделу.

Исследовав дифференциальный механизм поворота Четра на наличие избыточных связей было установлено, что таковые имеются. Механизм имеет 4 сателлита. При прямолинейном движении механизм имеет 7 избыточных связей. При этом при 3-х сателлитном исполнении нет избыточных связей влияющие только на распределение нагрузки между сателлитами, и имеет 4 избыточные связи. При 5-ти сателлитном исполнении 2 избыточные связи влияющие только на распределение нагрузки между сателлитами, и всего 10 избыточных связей.

При крутом повороте число избыточных связей остается таким же, как и при прямолинейном движении в силу конструкции, заторможенным звеном является коронная шестерня, в место солнечной.

Данный механизм имеет достаточно большой потенциал по применению конструкторских решений направленных на уменьшение числа избыточных связей.

На данный момент нет формул и рациональных зависимостей для оценки влияния уменьшения числа избыточных связей на увеличение долговечности (вопрос еще мало изучен). Однако внедрение самоустанавливающихся механизмов значительно увеличивает ресурс. Д. И. Шаткус в Таганрогском ГСКБ зерновых комбайнов использовал самоуста­навливающиеся сателлиты в редукторах комбайнов «Колос» и получил четырех­кратное увеличение долговечности.

Если данный механизм избавить от избыточный связей, рассматривая существующие аналоги, это даст увеличение долговечности до 2-3 раз.

Также данный механизм имеет возможность для установки 5-го сателлита. Если добавить 5-й сателлит это увеличит ресурс до 20%.

Приведённую выше последовательность оценки потенциальных возможностей можно рассматривать как методику, которую рекомендуется использовать при проектировании новых и анализе имеющихся зубчатых передач, как тракторов, так и других колёсных и гусеничных машин.

Раздел 4. Предлагаемые конструктивные решения по устранению избыточных связей.

4.1 ПП с упругим элементом

Задача полезной модели – создание планетарной передачи с повышенной надежностью и долговечностью.

Технический результат – повышение надежности и долговечности планетарной передачи вследствие выравнивания нагрузки между сателлитами и по длине их зубьев за счет упругого шарнирного соединения секторов сателлитного блока водила.

Указанный технический результат достигается тем, что в планетарной передаче, содержащей центральные колеса с внешним и внутренним зацеплением, сателлиты и водило, состоящее из секторов сателлитного блока и ступицы причем каждый сектор представляет часть дуги окружности, с одной стороны которого выполнена двузубая, а с другой однозубая вилки, секторы соединены последовательно с помощью осей, расположенных перпендикулярно плоскости дуги сектора, в средней части каждого сектора расположен сателлитный блок, состоящий из сателлита, оси и подшипника, при этом в промежутках между сателлитами расположены участки узкого шлицевого соединения, имеющего боковые и радиальные зазоры, при этом внутренние шлицы расположены в зоне однозубых вилок секторов, а внешние шлицы расположены на внешних поверхностях секторов венца ступицы, в каждом секторе со стороны однозубой вилки по окружности, проходящей через центры осей, в направлении к двузубой вилке выполнена выемка, в которой установлен опорный сухарь, поверхность которого, контактирующая с осью, выполнена в виде сектора цилиндра с радиусом, равным наружному радиусу оси, а противоположная плоская поверхность контактирует с установленным в выемке упругим элементом в виде пакета пластинчатых пружин, обеспечивающих в перпендикулярной осям плоскости упругую связь между шарнирно соединенными секторами для самоустановки сателлитного блока водила и выравнивания нагрузки между сателлитами и по длине зубьев.

Таким образом, в полезной модели впервые предложено использовать упругие шарнирные связи между сектором сателлитного блока водила, что обеспечивает самоустановку водила и выравнивания вследствие этого нагрузки между сателлитами и по длине их зубьев.

Планетарная передача содержит центральное колесо внешнего зацепления 1, размещенное в стакане 2 на подшипниках скольжения 3, центральное колесо внутреннего зацепления 4, установленное на подшипниках качения 5, опирающихся на стакан 2, установленный в расточке корпуса 6, водила 7, состоящего из составленного из секторов сателлитного блока 8 и ступицы 9.

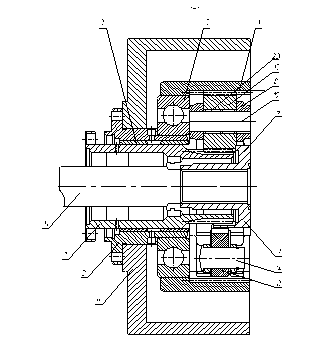
Рисунок 4.1 –общий вид планетарной передачи

Планетарный ряд образуют (рисунок 4.1) центральное колесо внешнего зацепления 1, которое является заторможенным, центральное колесо внутреннего зацепления 4, к которому подводится крутящий момент, сателлиты 10 и водило 7, предназначенное для передачи крутящего момента валу 11. Стакан 2 выполняет роль опоры центрального колеса внешнего зацепления 1 посредством подшипников скольжения 3, выполненных в виде бронзовых втулок, которые запрессовываются в отверстие стакана 2. Также стакан 2 служит опорой для центрального колеса внутреннего зацепления 4, установленного на нем через подшипник качения 5.

Сектор сателлитного блока 8 состоит из секторов 12 , представляющих часть дуги окружности, с одной стороны каждого из которых выполнена двузубая, а с другой однозубая вилки, сектора 12 связаны последовательно между собой с помощью цилиндрических шарниров 13 с осями 14, расположенными перпендикулярно плоскости дуги сектора по окружности между сателлитами 10 (рисунок 4.2).

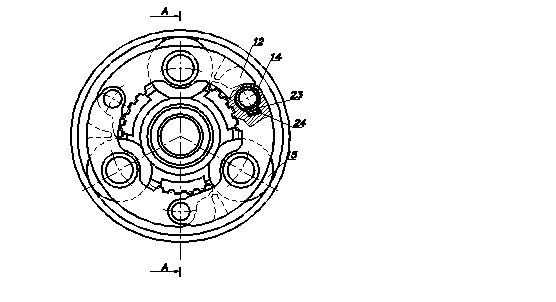
Рисунок 4.2 - водило

Для передачи крутящего момента ступице 9 на однозубой части вилки сектора выполнены участки внутренней поверхности шлицевого соединения 15. На внешних поверхностях секторов 16 (рисунок 4.5) венца ступицы 9 выполнены внешние участки узкого шлицевого соединения 17, зацепляющиеся с внутренней шлицевой поверхностью 15. Внутренние шлицы 15 расположены в зоне однозубых вилок секторов 12, а внешние шлицы 17 расположены на внешних поверхностях секторов 16 (рисунок 4.3) венца ступицы 9.

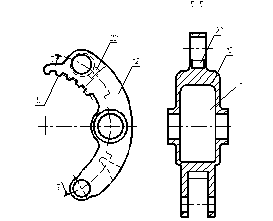
Рисунок 4.3 - сектор сателлитного блока Рисунок 4.4 – разрез по Б-Б

В средней части каждого сектора 12 в полости А (рисунок 4.4) расположен сателлитный блок, состоящий из сателлита 10 и оси 18 которая опирается на игольчатые подшипники качения 19.

Сателлитный блок 8 соединен охватываемой шлицевой поверхностью 20 со ступицей 9 (рисунок 4.5), поверхность 20 расположена в кольцевом объеме шлицевого соединения, ограниченного центральными колесами 1 и 4 и секторами 12 сателлитного блока 8.

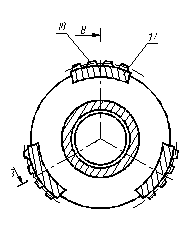
Рисунок 4.5 - ступица

Со стороны однозубых вилок 12 в материале секторов сателлитного блока 8 , служащем опорой осей 14, по окружности, проходящей через центры осей 14, в направлении к двузубым вилкам выполнены выемки 21, в которые установлены опорные сухари 22, поверхности которых, контактирующие с осями 14, выполнены в форме сектора цилиндра с радиусом, равным наружному радиусу осей 14, а противоположные плоские поверхности контактируют с установленными в выемки 21 упругими элементами в виде пакетов пластинчатых пружин 23 обеспечивающих в перпендикулярной осям плоскости упругую связь между шарнирно соединенными секторами для самоустановки сателлитного блока водила и выравнивания нагрузки между сателлитами и по длине зубьев.

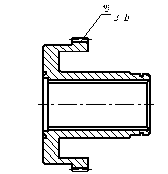
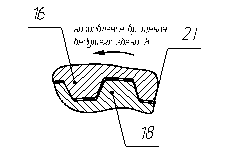
Рисунок 4.6 – ступица в разрезе Рисунок 4.7 – шлицевая поверхность

Таким образом, описанная полезная модель обеспечивает решение задачи создания планетарной передачи с повышенной надежностью и долговечностью вследствие выравнивания нагрузки между сателлитами и по длине их зубьев за счет упругого шарнирного соединения секторов сателлитного блока водила.

Для данного технического решения составлена структурная схема (рисунок 4.8). Расчет на избыточные связи произведен по формуле Малышева (4.1):

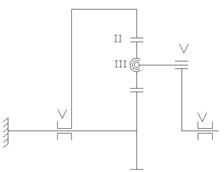
Рисунок 4.8– структурная схема

. (4.1)

Как видно по результатам расчета механизм имеет избыточные связи 2,3,4 при 3,4,5-ти сателлитах соответственно.

4.2 ПП с бочкообразными зубьями

Задача полезной модели – упрощение конструкции планетарной передачи и повышение надежности и долговечности.

Технический результат - повышение надежности и долговечности планетарной передачи вследствие самоустановки секторов сателлитного блока между центральными колесами, выравнивания нагрузки между сателлитами и по длине их зубьев за счет выполнения бочкообразного продольного профиля внешних шлицев и зубьев сателлитов.

Указанный технический результат достигается тем, что в планетарной передаче содержащей центральные колеса с внешним и внутренним зацеплением, сателлиты и водило, состоящее из составленного из секторов сателлитного блока и ступицы, причем каждый сектор представляет часть дуги окружности, с одной стороны которого выполнена двузубая вилка, а с другой однозубая вилка, секторы соединены последовательно с помощью осей, расположенных перпендикулярно плоскости дуги сектора, в средней части каждого сектора расположен сателлитный блок, состоящий из сателлита, оси и подшипника, при этом в промежутках между сателлитами расположены участки узкого шлицевого соединения, имеющие боковые и радиальные зазоры, при этом внутренние шлицы расположены в зоне однозубых вилок секторов, а внешние шлицы расположены на внешних поверхностях секторов венца ступицы, внешние шлицы и зубья сателлитов выполнены с бочкообразным продольным профилем для самоустановки секторов сателлитного блока между центральными колесами, выравнивания нагрузки между сателлитами и по длине их зубьев, при этом сателлитный блок, составленный из секторов, имеет не менее чем четыре сателлита.

Внешние шлицы и зубья сателлитов выполнены с бочкообразным продольным профилем, это позволяет секторам сателлитного блока, за счет того что они приобретают угловую подвижность, самоустанавливаться между центральными колёсами, выравнивать нагрузку между сателлитами и по длине их зубьев с учетом погрешностей изготовления всех элементов планетарной передачи.

Сателлитный блок, составленный из секторов, имеет не менее чем четыре сателлита, что позволяет получить дополнительную степень свободы, в противном случае образуется жесткая конструкция, которая не позволит в достаточной степени выравнивать нагрузку между сателлитами и самоустанавливаться секторам сателлитного блока между центральными колесами.

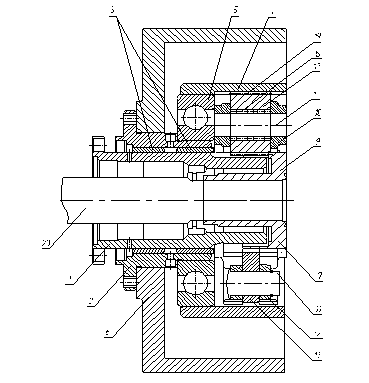
Рисунок 4.9 – общий вид планетарной передачи

Планетарная передача содержит центральное колесо внешнего зацепления 1 (рисунок 4.10), размещенное в стакане 2 на подшипниках скольжения 3, центральное колесо внутреннего зацепления 4, установленное на подшипниках качения 5, опирающихся на стакан 2, установленный в расточке корпуса 6, водило 7, состоящее из сателлитного блока 8 и ступицы 9.

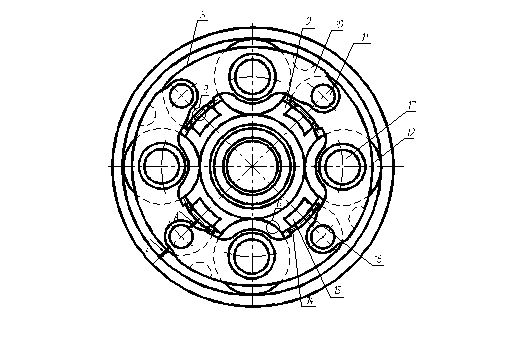
Рисунок 4.10 - водило

Сателлитный блок 8 состоит из секторов 10 (рисунок 4.10), представляющих часть дуги окружности, которые связаны последовательно между собою с помощью осей 11 , эти оси 11 (рисунок 4.11) расположены перпендикулярно плоскости дуги сектора 10 по окружности между сателлитами 12.

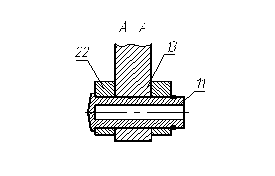
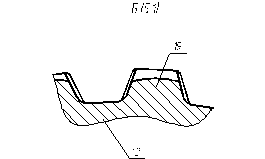
Рисунок 4.11 – ось Рисунок 4.12 - бочкообразный зуб

Для передачи крутящего момента ступице 9 на однозубой вилки 13 сектора 10 сателлитного блока 8 расположены внутренние шлицы 14. На внешних поверхностях секторов 15 венца ступицы 9 расположены внешние шлицы 16 (рисунок 4.13 и рисунок 4.14) с бочкообразным продольным профилем, зацепляющиеся с внутренними шлицами 14.

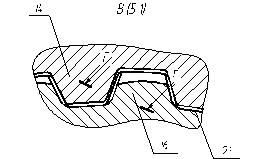
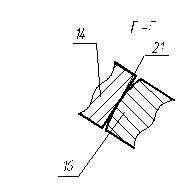
Рисунок 4.13 - шлицевое соединение Рисунок 4.14 - разрез по Г-Г

В середине каждого сектора 10 расположен сателлитный блок, состоящий из сателлита 12, оси 17 и подшипника 18. Зубья 19 сателлитов 12 выполнены с бочкообразным продольным профилем.

Планетарный ряд образуют центральное колесо внешнего зацепления 1, которое является заторможенным, центральное колесо внутреннего зацепления 4, к которому подводится крутящий момент, сателлиты 12 и водило 7, предназначенное для передачи крутящего момента валу 20. Стакан 2 выполняет роль опоры центрального колеса внешнего зацепления 1 посредством подшипников скольжения 3, выполненных в виде бронзовых втулок, которые запрессовываются в отверстие стакана 2. Также стакан 2 служит опорой для центрального колеса внутреннего зацепления 4, установленного на нем через подшипник качения 5.

Сателлитный блок 8, составленный из секторов 10, имеет не менее чем четыре сателлита 12, в противном случае образуется жесткая конструкция, которая не позволит в достаточной мере выравнивать нагрузку между сателлитами 12 и самоустанавливаться секторам 10 сателлитного блока 8 между центральными колесами 1 и 4.

Составленный из секторов 10 сателлитный блок 8 соединен участками узкого шлицевого соединения 21 со ступицей 9 (рисунок 4.15).

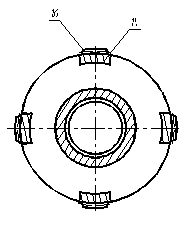
Рисунок 4.15 - ступица

Эти участки узкого шлицевого соединения 21, имеют достаточные боковые и радиальные зазоры, в совокупности с угловой подвижностью секторов 10 сателлитного блока 8, обусловленной наличием бочкообразного продольного профиля у внешних шлицев 16 и у зубьев 19 сателлитов 12, обеспечивают передачу крутящего момента от водила 7 к валу 20 планетарной передачи с самоустановкой секторов 10 сателлитного блока 8 между центральными колесами 1 и 4 и выравнивание нагрузки между сателлитами 12 и по длине их зубьев 19.

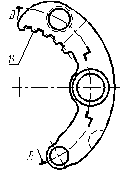
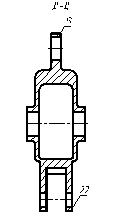
Рисунок 4.16 - сектор сетеллитного блока Рисунок 4.17 – разрез по Д-Д

С одной стороны сектора 10 сателлитного блока 8, располагается однозубая вилка 13 (рисунок 4.16), а с другой стороны - двузубая вилка 22 (рисунок 4.17).

Описанная конструкция планетарной передачи позволяет повысить надежность и долговечность передачи за счет того, внешние шлицы и зубья сателлитов выполнены с бочкообразным продольным профилем, для обеспечения самоустановки секторов сателлитного блока между центральными колесами и выравнивания нагрузку между сателлитами и по длине их зубьев и упростить передачу, вследствие отсутствия шаровых опор, соединяющих сектора сателлитного блока, которые представляются сложными в изготовлении и приводят к удорожанию производства.

Для данного изобретения составлена структурная схема (рисунок 4.18) и проведен расчет на избыточные связи по формулам Малышева (4.2).

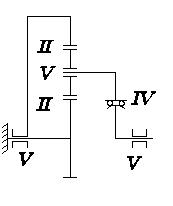
Рисунок 4.18 - структурная схема

. (4.2)

Данный механизм не имеет избыточных связей при 3,4,5 сателлитах.

4.3 ПП с карданным шарниром

Технический результат - повышение надежности и долговечности планетарной передачи вследствие самоустановки сателлитного блока между центральными колесами, выравнивания нагрузки между сателлитами и по длине их зубьев за счет последовательного соединения секторов сателлитного блока карданными шарнирами.

Указанный технический результат достигается тем, что в планетарной передаче, содержащей центральные колеса с внешним и внутренним зацеплением, сателлиты и водило, состоящее из составленного из секторов сателлитного блока и ступицы, причем каждый сектор представляет часть дуги окружности, секторы соединены последовательно, в средней части каждого сектора расположен сателлитный блок, состоящий из сателлита, оси и подшипника, при этом в промежутках между сателлитами расположены участки узкого шлицевого соединения, имеющие боковые и радиальные зазоры, при этом внутренние шлицы расположены на секторах сателлитного блока, а внешние шлицы расположены на внешних поверхностях секторов венца ступицы, секторы сателлитного блока соединены между собой карданными шарнирами для самоустановки сателлитного блока между центральными колёсами и выравнивание нагрузки между сателлитами и по длине их зубьев, с обеих сторон секторов сателлитного блока выполнены двузубые вилки, при этом с одной стороны внутренние шлицы расположены в зоне двузубых вилок параллельных плоскости секторов сателлитного блока, а с другой стороны двузубые вилки расположены перпендикулярно плоскости секторов.

Участки узкого шлицевого соединения ступицы и сателлитного блока, составленного из секторов, имеют осевые и радиальные зазоры, которые в совокупности с возможностями относительных поворотов секторов сателлитного блока за счет карданных шарниров позволяют сателлитному блоку самоустанавливаться между центральными колёсами, выравнивая нагрузку между сателлитами и по длине их зубьев.

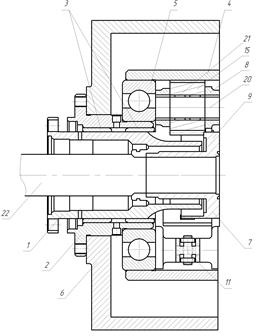
Рисунок 4.19 – Общий вид планетарной передачи

Планетарная передача содержит центральное колесо внешнего зацепления 1 (рисунок 4.19), размещенное в стакане 2 на подшипниках скольжения 3, центральное колесо внутреннего зацепления 4, установленное на подшипниках качения 5, опирающихся на стакан 2, установленный в расточке корпуса 6, водило 7, состоящее из сателлитного блока 8 и ступицы 9.

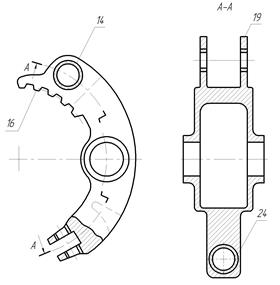
Рисунок 4.20 – сектор сателлитного блока Рисунок 4.21 – разрез по А-А

Сателлитный блок 8, состоит из секторов 10 (рисунок 4.20), представляющих часть дуги окружности, которые жестко связаны последовательно между собою с помощью карданных шарниров 11 (рисунок 4.23),состоящих из двух взаимно перпендикулярных поверхностей 12 и 13 и втулки 14, расположенными по окружности между сателлитами 15. Для передачи крутящего момента ступице 9 на двузубых вилках, параллельных плоскости секторов 10 сателлитного блока 8, расположены внутренние шлицы 16. На внешних поверхностях секторов 17 венца ступицы 9 выполнены внешние шлицы 18, зацепляющиеся с внутренними шлицами 16, расположенными на двузубых вилках 19, параллельных плоскости секторов 10 сателлитного блока 8 (рисунок 4.22).

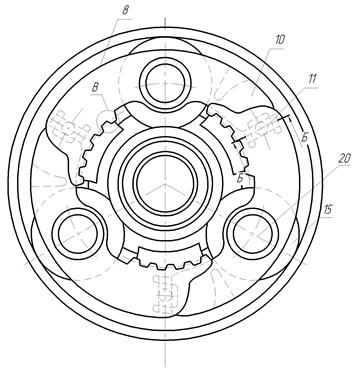
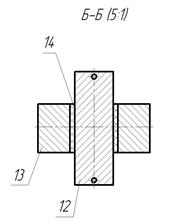
Рисунок 4.22- водило Рисунок 4.23 –карданный шарнир

В середине каждого сектора 10 расположен сателлитный блок, состоящий из сателлита 15, оси 20 и подшипника 21.

Планетарный ряд образуют центральное колесо внешнего зацепления 1, которое является заторможенным, центральное колесо внутреннего зацепления 4, к которому подводится крутящий момент, сателлиты 15 и водило 7, предназначенное для передачи крутящего момента валу 22, с которого он снимается.

Стакан 2 выполняет роль опоры центрального колеса внешнего зацепления 1 посредством подшипников скольжения 3, выполненных в виде бронзовых втулок, которые запрессовываются в отверстие стакана 2. Также стакан 2 служит опорой для центрального колеса внутреннего зацепления 4, установленного на нем через подшипник качения 5.

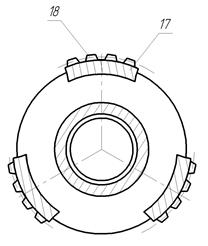
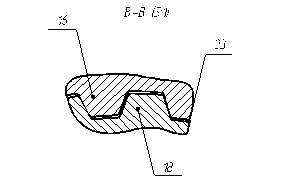
Рисунок 4.24 – ступица Рисунок 4.25 – шлицевое соединение

Сателлитный блок 8, составленный из секторов 10, соединен участками узкого шлицевого соединения 23 (рисунок 4.25) со ступицей 9 (рисунок 4.24). Эти участки узкого шлицевого соединения 23, имеющие достаточные боковые и радиальные зазоры, в совокупности с угловой подвижностью секторов сателлитного блока, обусловленной наличием карданных шарниров 11, обеспечивают передачу крутящего момента от водила 7 к валу 22 планетарной передачи с самоустановкой сателлитного блока в радиальном и угловых направлениях относительно центральных колес под воздействием сил, возникающих в зацеплениях сателлитов 15 с центральными колёсами 1 и 4 передачи и выравнивание нагрузки между сателлитами 15.

С одной стороны секторов 10 сателлитного блока 8, располагаются двузубые вилки 19, параллельные плоскости сектора 10 сателлитного блока 8, а с другой стороны - двузубые вилки 24, перпендикулярные плоскости секторов 10 сателлитного блока 8.

Для данного изобретения составлена структурная схема (рисунок 4.26) и проведен расчет на избыточные связи по формулам Малышева (4.3).

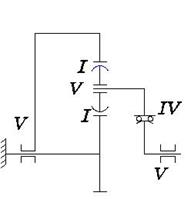
Рисунок 4.26 - структурная схема

. (4.3)

Данный механизм не имеет избыточных связей при 3,4,5 сателлитах.

4.4 Выводы к четвертому разделу

Результаты расчета предложенных вариантов показали, что предложенные кинематические схемы редукторов за счет исключения избыточных связей характеризуются гораздо меньшей интенсивностью нагрузок, вызванных погрешностями изготовления редуктора. Следовательно, можно заключить, что разработка и внедрение таких механизмов позволит существенно увеличить долговечность существующих трансмиссионных агрегатов, а также разработать новые более компактные трансмиссии.

Вариант планетарной передачи с упругим элементом дает 2,3,4 избыточные связи при 3,4,5 сателлитном исполнении соответственно, с карданным шарниром планетарная передача не имеет избыточных при 3, 4, 5 сателлитах, также как и планетарная передача с бочкообразными зубьями. Но именно планетарная передача с бочкообразными зубьями имеют самую простую и соответственно надежную конструкцию, также в ней используется меньшее количество деталей, чем в других планетарных передачах, что приводит к снижению стоимости производства при использовании данного механизма в сельскохозяйственном тракторе Четра-6.

Раздел 5. Предлагаемое изменение в ПМП трактора Четра-6

С целью уменьшения избыточных связей предлагается в конструкцию ПМП Четра-6 внести изменения. Для данной конструкции предлагаем применить техническое решение ПП с бочкообразными зубьями. Новая структурная схема механизма ПП изображена на рисунке 5.1.

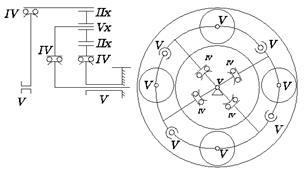
Рисунок 5.1 – структурная схема нового ПМП Четра-6

Проведем анализ этого механизма на избыточные связи по формулам Малышева

(5.1)

Как видно из результатов расчета по формулам данный механизм при 4-х сателлитах не имеет избыточных связей. Также имеет потенциал на установку 5-го сателлита, т.к. имеет 1-ну избыточную связь при 5 сателлитах.

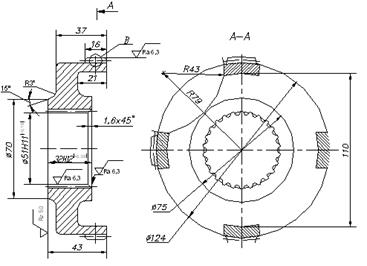
Рисунок 5.2 – ступица водила

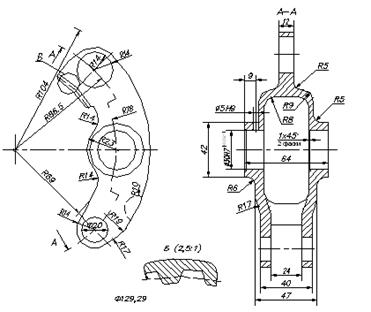
Рисунок 5.3 – сектор сателлитного блока

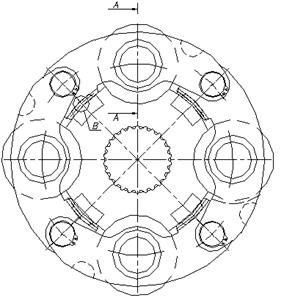
Рисунок 5.4 – водило в сборе с сателлитами.

На рисунках 4.2,4.3,4.4 показано водило спроектированное для ПМП Четра - 6. Данный механизм является статически определимой системой, то есть данный механизм является самоустанавливающимся, без избыточных связей. Это дает существенный прирост долговечности. Если сравнивать классический механизм и механизм Шаткуса (устранение 8 избыточных связей), увеличение долговечности в 3 раза. То применение водила в виде браслет (устранение 7 избыточных связей) оценочно даст увеличение долговечности в 2-3 раза по сравнению с ныне существующей планетарной передачи на Четре-6. Также если сравнивать ресурс, то из диссертации Морозова следует, что данный механизм способен дать около 11-12 тыс. моточасов, что превосходит ныне существующую планетарную передачу в Четре-6 в 2-2.5 раза.

Заключение

В данной работе были даны понятия избыточных связей в механизмах, показано влияние их на работоспособность планетарных передач, методы проверки на избыточные связи с учётом классов кинематических пар. Приведена программа экспертной оценки избыточных связей и эмпирическая формула их количественной оценки. Так же были посчитаны различные планетарные передачи и механизмы на избыточные связи.

Результатом работы является структурный анализ пмп Четра-6, выявление избыточных связей при 3,4,5 сателлитном исполнении, выявление особо вредных избыточных связей влияющих на распределение нагрузки между сателлитами. Конструирование нового водила в виде браслета для пмп Четра 6, применение которого делает данный планетарный механизм поворот статически определимым или самоустанавливающимся, то есть не имеющим избыточных связей, что подтверждает выполненный структурный анализ и расчет по формулам Малышева.

Так же было предложено 3 совершенно новых конструктивных решений по устранению избыточных связей планетарная передача с упругим элементом, планетарная передача с карданом и планетарная передача с бочкообразными зубьями. Последняя сконструирован в ПМП Четра-6. Данная конструкция должна не только равносильно заменять существующую, но и увеличивать ресурс её работы, а так, же давать возможность работать механизму в более нагруженных условиях, а это достигается за счет самоустанавливаемости, то есть избавления от избыточных связей, что было показано структурным анализом механизма и расчетом по формулам Малышева.