Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Фракталы— удивительные математические объекты, подкупающие своей простотой ибогатыми возможностями попостроению объектов сложной природы при помощи всего лишь нескольких коэффициентов ипростой итеративной схемы.

Именно эти возможности ипозволяют использовать ихдля сжатия изображений, особенно для фотографий природы ипрочих сложных самоподобных изображений.

Фрактал – структура, состоящая из частей, которые в каком-то смысле подобны целому. Фрактал выглядит одинаково, в каком бы масштабе мы его не наблюдали. Но, располагая только внешним видом, оценка фрактальных свойств затруднена, а в большинстве случаев невозможна.[1]

Основные свойства фрактальных множеств:

1. фрактал имеет тонкую структуру, то есть содержит произвольно малые масштабы;

2. фрактал слишком нерегулярное множество, чтобы быть описанным на традиционном геометрическом языке;

3. фрактал имеет форму самоподобия (приближенную или статистическую);

4. фрактальная размерность больше топологической размерности;

5. в большинстве случаев фрактал определяется очень просто, например, рекурсивно. [1]

Классификация фракталов.

Геометрические фракталы— самые наглядные фракталы, вдвухмерном случае ихполучают спомощью ломаной (или поверхности втрехмерном случае), называемой генератором. Заодин шаг алгоритма каждый изотрезков, составляющих ломаную, заменяется наломаную-генератор всоответствующем масштабе. Врезультате бесконечного повторения этой процедуры получается геометрический фрактал. [2]

Алгебраические фракталы— получают ихспомощью нелинейных процессов вn-мерных пространствах. Наиболее изучены двухмерные процессы.

Стохастические фракталы— получаются втом случае, если витерационном процессе хаотически менять какие-либо его параметры. При этом получаются объекты очень похожие наприродные— несимметричные деревья, изрезанные береговые линии ит.д. Двумерные стохастические фракталы используются при моделировании рельефа местности иповерхности моря. [2]

Существуют идругие классификации фракталов, например деление фракталов надетерминированные инедетерминированные. [2]

Классификация фракталов представлена См. Рисунок 1.

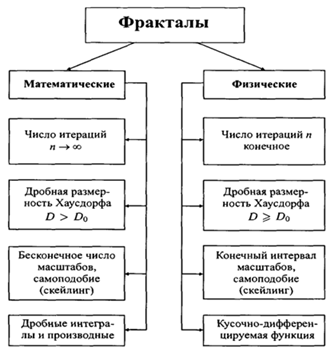
Рисунок 1 – Классификация фракталов

Фрактальный анализ оценивает фрактальные характеристики данных.

Он состоит из нескольких методов для присвоения фрактальной размерности и других фрактальных характеристик набору данных, который может быть теоретическим набором данных или шаблоном или сигналом, извлеченным из явлений, включая естественные геометрические объекты, экологию и водные науки, звук, колебания рынка, частота сердечных сокращений, частотная область в сигналах электроэнцефалографии , цифровых изображениях, молекулярном движении и науке о данных.

Фрактальный анализ сейчас широко используется во всех областях науки. Важным ограничением фрактального анализа является то, что достижение эмпирически определенной фрактальной размерности не обязательно доказывает, что модель фрактальна; скорее, необходимо учитывать другие существенные характеристики.

Фрактальный анализ ценен для расширения наших знаний о структуре и функциях различных систем и как потенциальный инструмент для математической оценки новых областей исследования. [2]

Фракталы имеют дробные измерения, которые являются мерой сложности , которая указывает степень которые объекты заполняют доступное пространство. Фрактальная размерность измеряет изменение «размера» фрактального множества с изменяющейся шкалой наблюдений и не ограничивается целыми значениями. Это возможно при условии, что меньшая часть фрактала похожа на целое, показывая одни и те же статистические свойства в разных масштабах. Эта характеристика называется масштабной инвариантностью, и может быть дополнительно классифицирована как самоподобие или самоаффинность, последняя масштабируется анизотропно (в зависимости от направления).

Независимо от того, расширяется ли фрактал или сужается, структура остается неизменной и выглядит столь же сложной. Фрактальный анализ использует эти основные свойства, чтобы помочь в понимании и характеристике сложных систем. Также возможно расширить использование фракталов за счет отсутствия единой характерной временной шкалы или паттерна. [3]

Цвет и текстура являются важными характеристиками изображения. Анализ цветных текстур включает в себя их описание и классификацию, т.е. формирование кластеров и сегментацию (разбиение изображения на области, которые являются однородными относительно одной или нескольких характеристик либо принадлежат некоторому кластеру).

Под кластером понимается группа объектов, образующих в пространстве описания компактную в некотором смысле область.

Так, фракталы используются при анализе текстурных изображений ландшафтов, полученных при аэрокосмической съемке, при анализе поверхностей порошков и других пористых сред, при анализе облаков и т.д.

Размер фрактала представляет собой характеристику сложности поверхности и принимает значения в диапазоне от 2 до 3: меньшим значениям размера фрактала соответствуют гладкие поверхности, а большим — более сложные изрезанные поверхности. [4]

При сегментации цветных текстур необходимо учитывать как пространственные характеристики, так и характеристики цветности. Эффективность выбора признаков зависит от выбора цветового координатного пространства, при этом наиболее информативным из цветовых признаков является компонент тона. Осуществляется преобразование цветового координатного пространства RGB в пространство LSH.

Оценка размера фрактала производится по яркостному компоненту изображения. Хотя размер фрактала инвариантен к изменению масштаба, природные поверхности не обладают одинаковым размером фрактала во всем возможном диапазоне масштабов. Оценка фрактальности текстуры является важной характеристикой при сегментации изображений по размеру фрактала. Фрактальность текстуры оценивается по монотонности изменения характеристики фрактала в зависимости от шага оценивания. Диапазон допустимых значений шагов определяется интервалом монотонности.

Размер фрактала цветной текстуры во многом зависит от выбора метода оценивания. Сопоставление текстур возможно при использовании одного и того же метода (группы методов). Более того, не всякие текстуры хорошо различимы по размеру фрактала. В связи с этим прежде чем включать в систему признаков размер фрактала, необходимо оценить фрактальность текстуры.

Оценка фрактальности текстуры производится на основе выбранного метода оценивания размера фрактала.

Размер фрактала оценивается по формуле

D = K-01 (1)

где K=2 или 3 в зависимости от алгоритма оценивания, 01 — тангенс угла наклона линии выборочной регрессии.

Поскольку размер фрактала вычисляется через оценку выборочной регрессии, то естественно оценивать фрактальность текстуры по коэффициенту корреляции между логарифмом случайной величины и логарифмом заданной функции шага. [4]

При этом для принятия решения о фрактальности текстуры необходимо произвести следующие действия:

I. построить зависимость коэффициента корреляции от задаваемого шага; значение шага, при котором функция имеет максимум, является максимальным;

II. при использовании методов, в которых оценка размера фрактала принимается как среднее значение для серии экспериментов, не учитывать размер фрактала при низких значениях коэффициента корреляции;

III. при низких значениях коэффициента корреляции не включать размер фрактала в систему признаков для сегментации текстур. [4]

Метрика— функция, заданная напространстве, возвращающая расстояние между двумя точками этого пространства. Например, привычная нам Эвклидова метрика. Если напространстве задана метрика, оно называется метрическим. Метрика должна удовлетворять определенным условиям, нонебудем углубляться. [5]

Сжимающее отображение (преобразование)— функция наметрическом пространстве, равномерно уменьшающая расстояние между двумя точками пространства. [5]

Несколько аффинных сжимающих отображений образуют систему итерированных функций (СИФ). Посути, СИФ— это множительная машина. Она принимает исходное изображение, искажает его, перемещает, итак несколько раз.
Например, вот так при помощи СИФ изтрех функций строится треугольник Серпинского. ( Рисунок 2 ) [5]

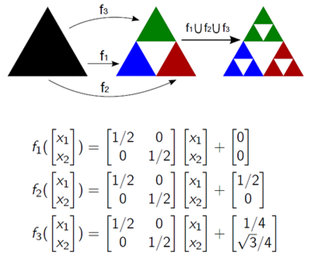
Рисунок 2 – Треугольник Серпинского

Исходный треугольник три раза множится, уменьшается ипереносится. Итак далее. Если так продолжать добесконечности, получим известный фрактал площадью 0иразмерностью 1,585.

Если функции, входящие вСИФ,— сжимающие, тосама СИФ тоже имеет неподвижную точку. Вот только эта «точка» будет уже непривычной нам точкой вN-мерном пространстве, амножеством таких точек, тоесть изображением. Оно называется аттрактором СИФ. Для СИФ, приведенной выше, аттрактором будет треугольник Серпинского.

Переходим впространство изображений. Вэтом пространстве:

· Точка пространства— это изображение.

· Расстояние между точками показывает, насколько похожи изображения между собой, насколько «близки» (естественно, если его задать соответствующим образом).

· Сжимающее отображение делает два любых изображения более похожими (всмысле заданной метрики). [5]

Имея СИФ, найти аттрактор просто. Вовсяком случае, имея под рукой компьютер. Можно взять абсолютно любое начальное изображение иначать применять кнему СИФ. Пример стемже треугольником, ноуже построенным изквадрата ( Рисунок 3 ).

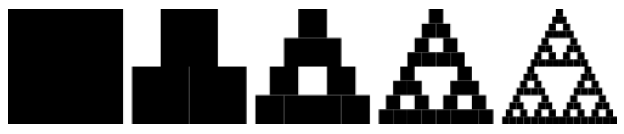
Рисунок 3 – Применение СИФ на квадрат

Получается, что для построения довольно сложной фигуры нам потребовалось 18коэффициентов. Выигрыш налицо.

Еслибыумели решать обратную задачу— имея аттрактор, строить СИФ. Тогда достаточно взять аттрактор-изображение, похожее нафотографию вашей кошки иможно довольно выгодно его закодировать.

Вот здесь начинаются проблемы. Произвольные изображения, вотличие отфракталов, несамоподобны, так что так просто эта задача нерешается.

Самоподобие нам нужно обязательно— иначе ограниченные всвоих возможностях аффинные преобразования несмогут правдоподобно приблизить изображения. Аесли его нет между частью ицелым, томожно поискать между частью ичастью. [5]

Упрощенная схема кодирования выглядит так:

1. Изображение делится нанебольшие неперекрывающиеся квадратные области, называемые ранговыми блоками. Посути, разбивается наквадраты.

2. Строится пул всех возможных перекрывающихся блоков вчетыре раза больших ранговых— доменных блоков.

3. Для каждого рангового блока поочереди «примеряем» доменные блоки иищем такое преобразование, которое делает доменный блок наиболее похожим натекущий ранговый.

4. Пара «преобразование-доменный блок», которая приблизилась кидеалу, ставится всоответствие ранговому блоку. Взакодированное изображение сохраняются коэффициенты преобразования икоординаты доменного блока. Содержимое доменного блока нам никчему— выже помните, нам все равно скакой точки стартовать.

НаРисунке 4 ранговый блок обозначен жёлтым, соответствующий ему доменный— красным. Также показаны этапы преобразования ирезультат.
Недостаток схемы виден невооруженным глазом.

Сколько доменных блоков размером 32×32 содержит двухмегапиксельное изображение ?

Полный ихперебор для каждого рангового блока иесть основная проблема такого вида сжатия— кодирование занимает очень много времени.

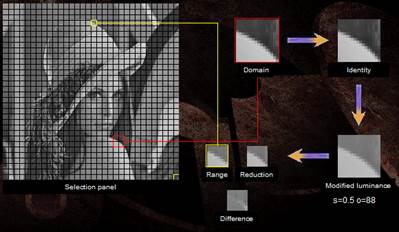
Рисунок 4 – Кодирование изображения

Декодированиеже производится просто идовольно быстро. Берем любое изображение, делим наранговые области, последовательно заменяем ихрезультатом применения соответствующего преобразования ксоответствующей доменной области.