Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Довольно часто возникает необходимость узнать величину тока в нейтральном (по-старому нулевом) проводе при неравномерной нагрузке в трехфазной сети. Существующие методы графический или математический очень неудобны.

Графический – из-за необходимости чертежных работ, а математический - по причине необходимости применения комплексных чисел и логарифмов.

Пришлось разработать простой порядок расчета, в котором, для наглядности, показан графический метод, но сам расчет выполнен тригонометрическим методом.

Итак, посмотрим схему трехфазной сети (Рисунок 1), на которой, в качестве примера, токи в фазах А, В и С равны 10, 30 и 20 А соответственно.

На векторной диаграмме слева мы видим векторы этих токов и добавленные вертикальную ось Y и горизонтальную ось Х. В правой части диаграммы показано сложение этих векторов путем переноса параллельно самим себе и присоединения начала следующего вектора к окончанию предыдущего.

Вектор тока в нейтральном проводе IN, полученный как результат сложения показан вместе со своими проекциями на ось Х - INX и ось Y - INY.

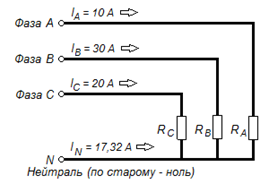
Рисунок 1 – Схема неравномерной трехфазной нагрузки в нейтральном проводе

Тригонометрический расчет мы начнем как раз с определения проекций тока в нейтральном проводе путем суммирования проекций токов фаз А, В и С на оси X и Y

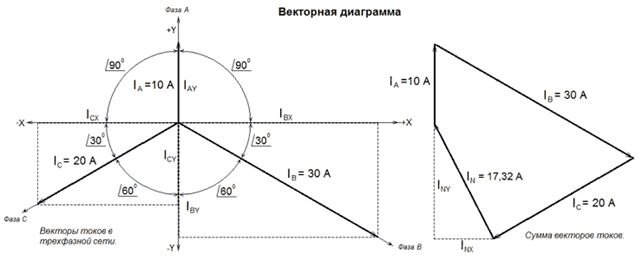
Рисунок 2 – Векторная диаграмма

Так, проекцию тока фазы В на ось Х - IBХ можно считать катетом, величина которого является произведением полного значения тока IB (гипотенузы) на косинус угла 30О.

IBХ = IB · cos30О,

подставив значения – получим:

IBХ = 30 · 0,866025 = 25,98

Проекцию тока фазы В на ось Y - IBY можно считать вторым катетом, величина которого является произведением полного значения тока IB (гипотенузы) на косинус угла 600, но при этом, глядя на векторную диаграмму, следует учесть, что эта проекция находится в области отрицательных значений оси Y, поэтому для получения отрицательного числа добавляем в формулу (-1).

IBY = IB · cos60О · (-1),

подставив значения – получим

IBY = 30 · 0,5 · (-1) = - 15.

Для фазы С все проекции находятся в области отрицательных значений и по аналогии с фазой В формулы расчета будут следующими:

ICX = IC · cos30 · (-1),

подставив значения – получим

ICX = 20 · 0,866025 · (-1) = - 17,32.

ICY = IC · cos60О · (-1),

подставив значения – получим

ICY = 20 · 0,5 · (-1) = - 10.

C фазой А совсем просто.

IAX = 0, IAY = 10.

Сложив все проекции по оси Х, мы получим Х – проекцию тока в нейтральном проводе, а по оси Y, его Y - проекцию.

INX = IAX + IBX + ICX = 0 + 25,9875 – 17,3205 = 8,66.

INY = IAY + IBY + ICY = 10 - 15 – 10 = -15.

Полное значение тока в нейтральном проводе вычисляем по теореме Пифагора как корень квадратный от суммы квадратов катетов INX и INY.

В случае, если нам известны только мощности по каждой фазе, значения токов в фазе А,В и С можно узнать введя значения мощностей в форму расчета тока при однофазной нагрузки, которая размещена в начале статьи. При этом не забываем, что косинус фи для активной нагрузки равен единице.

Конечно, можно было бы разработать расчет в котором учитывались бы и реактивные нагрузки, но это привело бы к его значительному усложнению, да и к тому же подавляющая часть нагрузок в обычных сетях является активной, потому значащих отклонений реальных токов от полученных в данном расчете быть не должно.