В задачах четкого и нечеткого линейного программирования необходимо среди допустимых решений выбрать оптимальное по одному заранее выбранному критерию. Между тем, в реальных экономических задачах приходится искать наилучшее решение, руководствуясь несколькими различными целями. Так, в промышленном производстве важными показателями эффективности являются: рост производительности труда, прибыль, рентабельность и другое. Максимальное значение одного из показателей еще не означает, что то или иное предприятие работает лучше. Только система показателей может характеризовать эффективность всего производства [1–3].
Задачи, решаемые с учетом множества показателей или критериев, носят название многокритериальных. Если разновидность критериев выражена слабо и пользователь готов допустить снижение значений более важных критериев, чтобы добиться повышения значений менее важных критериев, то для решения многокритериальной задачи прибегают к методу уступок [1–3].
Решение задач нечеткого линейного программирования (НЛП) при нечеткой информации основывается на аппарате нечеткой математики [4], нечеткой логики [5] и нечеткой геометрии [6; 7].
В данной работе мы предлагаем рассмотрение решения многокритериальных задач НЛП методом последовательных уступок с использованием аппарата нечеткой математики и нечеткой геометрии.
Математически задача НЛП содержит нечеткую область допустимых решений, которая может иметь любую природу, и несколько нечетких целевых функций, значение которых должно максимизировать или минимизировать в данной области. Максимизация и минимизация нечетких целевых функций легко сводится друг к другу, умножением на –1, поэтому, не нарушая общности, можно считать, что данная задача имеет вид:
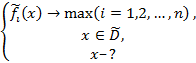(1)
Где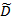 
– нечеткая область допустимых решений.
В экономических задачах нечеткая область допустимых значений, обычно задается системой нечетких уравнений и неравенств [6].
Метод последовательных уступок решения нечетких многокритериальных задач применяется в том случае, когда частные критерии упорядочены в порядке убывания важности. Сформулируем алгоритм этого метода.
1. Расположить нечеткие критерии по их значимости (наиболее важный считается первым).
2. Решить задачу по первому нечеткому критерию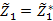 
, то есть отыскать экстремальное значение 
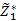целевой функции 
.
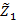3. Сделать уступку по первому нечеткому критерию, иными словами, уменьшить величину 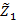до значения 
.
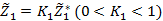4. В задачу ввести дополнительное ограничение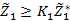 
.
5. Решить задачу по второму критерию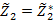 
.
6. Обратится к пункту 3, сделать уступку для второго критерия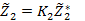 
.
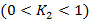7. Ввести в задачу дополнительное ограничение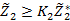 
.
8. Новую задачу, уже с двумя нечеткими ограничениями, решить по третьему критерию и т.д.
9. Процесс итерации заканчивается, когда решение будет получено ко всем критериям.
Проведем геометрическую интерпретацию этого метода. Нечеткие прямые и отрезки будем изображать их модальными значениями (ядрами), а нечеткость (размытость) нечетких прямых и отрезков будем изображать крайними значениями их коэффициентов концентрации.
Пример. Решить задачу по двум критериям, считая первый наиболее предпочтительным. Его отклонение от максимального составляет не более 25%.
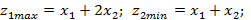
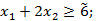
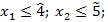
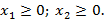
Где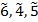 
– нечеткие гауссовы числа, со следующими функциями принадлежности соответственно:
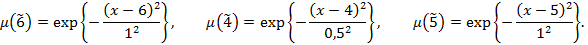
Решение. Используя первый критерий, находим нечеткую область допустимых решений 
. Максимальное нечеткое значение целевой функции достигается в нечеткой точке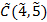 
, представленной на графике (рис. 1).
Делаем уступку на 25%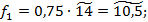 
получаем дополнительное ограничение 
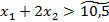(на рис. 1 – нечеткая прямая IV). Здесь 
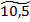– нечеткое гауссово число с функцией принадлежности
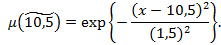
С учетом дополнительного ограничения нечеткой областью решения является нечеткий треугольник 
. Минимальное значение целевой функции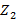 
достигается в нечеткой точке 
.
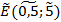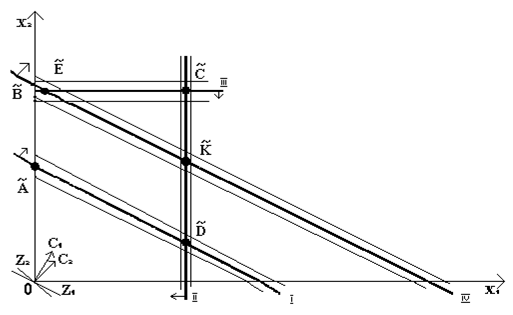
Рис. 1. Графическое решение нечеткой многокритериальной задачи.
Таким образом, план в нечеткой точке 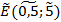будетет наиболее эффективным при данных условиях: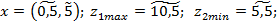 
Где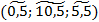 
– нечеткие гауссовы числа с соответствующими функциями принадлежности:
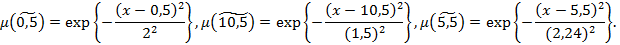
Выводы. В данной работе проведено рассмотрение решения задач многокритериального нечеткого линейного программирования методом последовательных уступок и проведена геометрическая интерпретация этого метода с использованием нечеткой математики и нечеткой геометрии.
Библиографическая ссылка
Волошин В.А., Барышевский С.О. РЕШЕНИЕ МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧ НЕЧЕТКОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК // Международный студенческий научный вестник. – 2020. – № 3. ;URL: https://eduherald.ru/ru/article/view?id=20133 (дата обращения: 21.11.2024).