Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Пушка В.С. 1 Матвеева Т.А. 1 Светличная В.Б. 1 Соколова А.В. 1

---

1 Волжский политехнический институт

К транспортным задачам относится широкий круг задач с общей математической моделью, они определяются как задачи линейного программирования специального вида и решаются оптимальными методами. В классическом виде транспортной задачи выделяют два типа: по критерию стоимости (минимизируются затраты на перевозку) и по критерию времени (минимизируется время на перевозку грузов). Мы рассматриваем класс задач по минимизации общей стоимости перевозок грузов из пунктов отправления в пункты потребления. По теории сложности вычислений транспортная задача входит в класс сложности P. В работе рассмотрены методы решения транспортных задач. Существует ряд методов построения начального опорного решения, наиболее простым из них является метод северо-западного угла. Далее для анализа полученного плана и его последующего улучшения вводятся дополнительные характеристики пунктов отправления и назначения, называемые потенциалами. Такой метод улучшения плана перевозок называется методом потенциалов. При этом на каждом этапе строится разгрузочный цикл, который позволяет снижать расходы на перевозку. Транспортная задача применяется в случаях: оптимизации поставок сырья и материалов на производственные предприятия; оптимизации доставок товаров со складов в розничные магазины; оптимизации пассажирских перевозок, и т.п.

Статья в формате PDF

0 KB

транспортная задача

метод северо-западного угла

метод потенциалов

план перевозок

1. Агишева Д.К., Зотова С.А., Светличная В.Б., Матвеева Т А. Транспортные и сетевые модели управления. Часть 2: учебное пособие / С.А. Зотова, Д.К. Агишева, В.Б. Светличная, Т.А. Матвеева; ВПИ (филиал) ВолгГТУ. – Волгоград: ИУНЛ ВолгГТУ, 2012. – 160 с.

2. Агишева Д.К., Зотова С.А., Матвеева Т.А., Светличная В.Б. Линейное программирование (учебное пособие) // Успехи современного естествознания. – 2010. – № 9 – С. 61–62 URL: www.rae.ru/use/section=content&op=show_article&article_id=7785125.

3. Казачков А.Д., Агишева Д.К., Светличная В.Б., Зотова С.А. Реализация метода северо-западного угла на Mathcad 15 // Материалы VIII Международной студенческой электронной научной конференции «Студенческий научный форум» www.scienceforum.ru/2016/1762/23702.

Транспортная компания занимается перевозкой зерна специальными зерновозами от трёх элеваторов к четырём мельницам. В табл. 1 показаны возможности отгрузки зерна элеваторами, а также стоимость перевозки зерна одним зерновозом от элеваторов к мельницам. Стоимость перевозок приведена в ден. ед. [1].

Требуется определить структуру перевозок между элеваторами и мельницами с минимальной стоимостью. Для этого необходимо найти матрицу перевозок, при которой стоимость всех расходов на доставку груза окажется минимальной. Заполним транспортную таблицу (табл. 1).

Начальное решение получим, например, методом северо-западного угла (табл. 2) [3].

Таблица 1

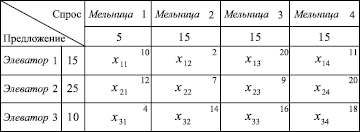
Таблица 2

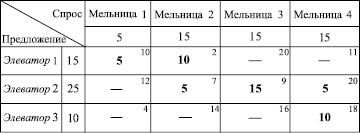
Суммарная стоимость перевозок равна

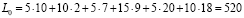(ден. ед.).

Для нахождения оптимального решения используем метод потенциалов [1, 2]. Вычисления обычно выполняются непосредственно в транспортной таблице (табл. 3). Положим 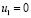. Поскольку все потенциалы определены, далее вычислим косвенные стоимости 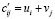для всех свободных клеток и запишем найденные значения в левом верхнем углу каждой незанятой клетки. В левом нижнем углу записываем разности 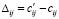для каждой небазисной переменной .

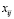Таблица 3

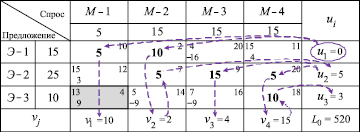
Определив вводимую в базис переменную 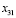, найдём исключаемую из базиса переменную. Необходимо, чтобы перевозки по маршруту, соответствующему переменной 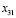, уменьшили общую стоимость перевозок. Какой объём груза можно перевезти по этому маршруту? Обозначим через ε 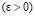количество груза, перевозимого по маршруту (3;1) (т. е. 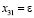). Сначала построим замкнутый цикл, который начинается и заканчивается в ячейке, соответствующей вводимой переменной 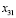. Для ячейки (3;1) определим цикл, включающий клетки с базисными поставками: (3;1), (1;1), (1;2), (2;2), (2;4) и (3;4) (табл. 4).

Для перераспределения поставок по найденному циклу необходимо определить минимальный перевозимый груз ε [1]. Чтобы выполнились ограничения по спросу и предложению, надо поочерёдно отнимать и прибавлять величину ε к значениям базисных переменных, расположенных в угловых ячейках найденного цикла (табл. 5).

Искомую величину следует выбирать среди клеток, содержащих знак «минус», т.е.

.

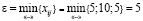Переменные 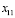и 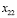обращаются в нуль. Поскольку только одна переменная исключается из базиса, то в качестве исключаемой можно выбрать как 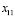, так и 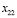. Остановим свой выбор на 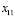. Тогда 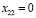. Определив значение для вводимой переменной 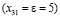, и выбрав исключаемую переменную, откорректируем значения базисных переменных, соответствующих угловым ячейкам замкнутого цикла (табл. 6).

Таблица 4

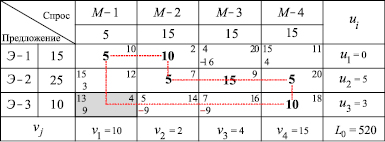
Таблица 5

Таблица 6

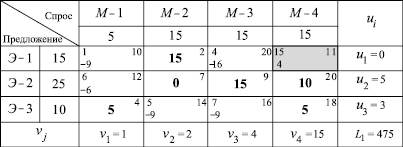
Перевозка единицы груза по маршруту (3;1) уменьшает общую стоимость перевозки на 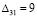ден. ед. Суммарная стоимость перевозок будет на 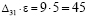ден. ед. меньше, чем в предыдущем решении.

Так как , то получим

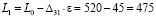ден. ед.

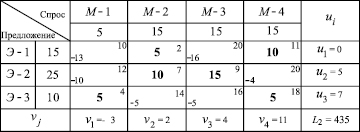
Продолжим анализ оптимальности. Вычислим потенциалы нового базисного решения (табл. 7). Новой вводимой в базис переменной будет 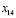. Замкнутый цикл позволяет найти её значение x14=10 и исключаемую переменную .

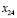Новое решение, представленное в табл. 8, уменьшает значение целевой функции на 40 (ден. ед.). Тогда ден. ед.

Таблица 7

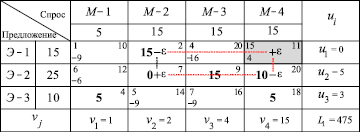
Таблица 8

Теперь для всех небазисных переменных 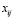оценки 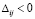. Т.е. выполнился критерий оптимальности на минимум [2]. Таким образом, найденное решение является оптимальным.

,

.

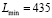Полученное решение, изложенное в терминах исходной задачи перевозки зерна от элеваторов до мельниц, имеет следующий смысл:

Суммарная стоимость перевозок 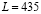ден. ед.

Библиографическая ссылка