Теория вероятностей берёт свое начало в первой четверти XVII в. Поскольку область ее применения XVII-XVIII вв. из-за невысокого уровня естествознания ограничивалась узким кругом вопросов, таких как страхование, азартные игры, демография, то теория вероятностей в то время не смогла получить молниеносного развития. Однако с XIX в. в связи с практической необходимостью, теория вероятностей стремительно развивается и находит применение в различных сферах науки, экономики, техники. Например, теория ошибок наблюдений, теория стрельбы, статистика, молекулярная и атомная физика, химия, метеорология, вопросы планирования, статистический контроль в производстве и так далее.
В наши дни нет области знаний, в которых не использовались бы методы, например, стохастики, включающей в себя части теории вероятностей и математической статистики.
Использование вероятностно-статистических способов является традиционным в физике, геодезии, биологии, экономике, лингвистике, психологии, теории обучения и так далее. Теория вероятностей – математическая основа статистики – науки XX века, а развитие статистических и кибернетических идей способствовало значительному возрастанию прикладного значения теории вероятностей [8].
В XVII веке французы П. Ферма, Б. Паскаль и голландец Х. Гюйгенс впервые попытались дать определение вероятности. В середине XIX века благодаря работам известного математика и механика П. Чебышева и его последователей А. Ляпунова и А. Маркова теорию вероятностей в мире стали величать «русской наукой». Данные исследования продолжили С. Бернштейн, А. Хинчин и А. Колмогоров, Б. Гнеденко, Ю. Прохоров, Б. Севастьянов, Ю. Линник и другие [9].
По мнению Лапласа «теория вероятностей – это здравый смысл», который сведен к исчислению. Пьер-Симон говорил о ней, что «нет науки, более достойной наших размышлений» и что «было бы полезно ввести ее в систему народного просвещения». Его призыв услышало общество и в программу средней школы включена стохастическая линия.
В современном мире для решения многих задач в экономической сфере и сфере финансов применяются различные методы математики и статистики, основывающиеся на базовых понятиях и законах теории вероятностей. В условиях современной экономической ситуации теория вероятностей является важной частью в повышении квалификации профессионалов в области экономики и финансов [3].
Теория вероятностей считается первостепенной среди математических наук, которая изучает законы, управляющие случайными величинами.
В России заинтересованность теорией вероятностей возникла в начале XIX в. Большую пользу в развитие этой науки привнесли такие русские ученые, как П.Л. Чебышев, А.М. Ляпунов, А.А. Марков.
Теория вероятностей – наука, изучающая применение специфических методов, способствующих решению задач, возникающих в процессе рассмотрения случайных величин. Она выявляет закономерности, относящиеся к массовым явлениям. Данные методы не определяют итог случайного явления, но могут показать суммарный результат. Таким образом, если мы изучим законы, которые управляют случайными событиями, то сможем при необходимости изменить исход этих событий.
Одной из первостепенных областей применения теории вероятностей является экономика. Планирование, исследование и прогнозирование экономических явлений невыполнимы без создания экономико-математических моделей, опирающихся на теорию вероятностей.
Коммерческие банки в настоящее время управляют широким спектром операций денежно-кредитного характера, но их основная деятельность – выдача кредитов. В настоящее время у банков возникает опасность – кредитный риск. Он обуславливается вероятностью выполнения кредитозаемщиком всех обязательств соглашения по объемам и срокам. Степень вероятности формируется способностью заёмщика погашать кредитные обязательства [10].
Рассмотрим пример 1. Человек, взявший кредит, должен его вернуть. Однако он возвращает деньги частями, также выплачивает фиксированный процент за пользование кредитом. По прошествии определенного времени кредитозаемщик должен вернуть всю сумму, которую он брал в кредит, а также плату за его пользование. Но при некоторых обстоятельствах, когда он не может выполнить условия договора, банк с помощью судебного иска накладывает взыскание и компенсирует свои потери. Однако главной задачей для банка является выдача кредитов и извлечение из этого прибыли, а не наложение штрафов. Ввиду этого банкам выгоднее выдавать кредиты только тем, в ком он может быть уверен, что ссуда будет возвращена точно в срок и с процентами.
Появляется случайная величина – возвращен кредит или нет. Для того чтобы узнать, надежен ли кредитуемый или нет, банк анализирует общую характеристику, личные доходы, собственный капитал, экономическую ситуацию в целом. В этот перечень так же относится кредитовая история заемщика, процент людей, которые вернули денежные средства в определенный срок того социального положения, к которому относится заемщик и так далее. Анализ проводится методами теории вероятностей и математической статистики. Несмотря на это банк своей главной целью ставит получение прибыли, а не компенсацию, полученную с людей, которые не смогли выплатить кредит, поэтому каждой банковской организации выгоднее предоставлять кредиты в тех ситуациях, когда имеются гарантии выплаты кредитованной суммы.
Таким образом, образуется величина, которая случайна и показывает возможность человека погасить кредит. Для того чтобы определить категорию граждан, которым можно выдать кредит, кредитная организация рассматривает и изучает статистику. Проводится анализ процентного соотношения в срок вернувших кредитов и всю кредиторскую историю в целом. Методами и способами математической статистики и теории вероятностей происходит анализ и оценка.
Проанализируем задачу 2 на определение кредитной ставки. Кредитная организация G выдает кредит 1000000 рублей на 1 год. Вероятность не погашения ссуды 1 %. Определите размер процентной ставки для получения прибыли.
Обозначим процентную ставку p (100 %). Доход кредитной организации обозначим случайной величиной, так как заёмщику нужно вернуть кредит в совокупности с процентами, но при этом он может его не вернуть. Составим закон распределения, где р – условия возврата кредита с процентами, а прибыль банка получается р млн руб:
|
р |
–1 |
|
0,99 |
0,01 |
Таким образом, вероятность возврата 99 %.
1 % невозврата, когда банк теряет 1000000 рублей, показываем как доход, равный –1.
Определим математическое ожидание:
.
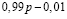Следовательно, решив неравенство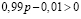 
, мы придем к тому, что 
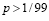, тогда ставка процента по кредиту должна быть выше, чем 1 % (100/99).
Главным риском при выдаче кредита значится вероятность того, что заёмщик не сможет вовремя выполнить обязательства. Ликвидный и процентный риск зависят от кредитного. Это обуславливается, в первую очередь, тем, что основной причиной кризиса ликвидности является очень высокий уровень кредитного риска, проявляющийся в том, что большие суммы кредитов не погашаются. Договоры о ссудах не обеспечивают колоссальных доходов, так как заемщики не возвращают больше, чем прописано в договоре, очень часто кредитуемые возвращают меньше, чем было указано в договоре. Частично возвращенная сумма или долг при погашении ведут к уменьшению дохода банка и кредитному риску.
Рассмотрим задачу 3. Пусть банковская организация W привлекла сумму в 60 ден. ед., сроком хранения 0,2 года (73 дня), ставка процента годовых – 30 % и внес в полном размере в кредит сроком погашения 0,2 года и процентной ставкой 50 % годовых. Чистый доход, который получит банк за 73 дня (0,2 года) при совершении этой депозитно-кредитной операции и при кредитном риске равном 0, получится:
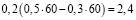ден.ед.
Сделаем предположение – вероятность не погашения кредита 20 %, следовательно, сумма прибыли, с учетом появившегося кредитного риска:
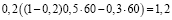ден.ед.
Анализ результатов подсчетов позволяет сделать вывод: если уровень кредитного риска 20 %, то доход понижается. Таким образом, для покрытия убытка в прибыли, банковской организации нужно повысить кредитную ставку процента.
Банк является одним из главных и надежных институтов в мире, который являет собой основу стабильной и развитой системы экономики.
На сегодняшний день имеет место быть нестабильная экономическая и правовая атмосфера банковского института, при которой банкам необходимо обязательно сохранять и увеличивать вложенные суммы вкладчиков. Кредитные операции – это основа банковской системы. Именно они являются главной частью банковской прибыли.
В нынешних условиях рыночной экономики, в ситуации связанной с экономическими рисками максимальную прибыль получает умеющий рассчитать, заметить и распознать кредитные риски, спрогнозировать их и минимизировать. Это главная причина успешности банка в кредитно-денежной политике. Банк, анализируя все статистические денежные характеристики клиента, способен не только охарактеризовать кредитоплатежность фирмы, но и помочь в активизации резервов бизнеса и, как следствие, стать более надежным заёмщиком.
Библиографическая ссылка
Заргарян Н.Р., Лубянская М.В. ПРИМЕНЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ В СФЕРЕ КРЕДИТОВАНИЯ // Международный студенческий научный вестник. – 2018. – № 3-1. ;URL: https://eduherald.ru/ru/article/view?id=18208 (дата обращения: 21.11.2024).