Главным вопросом линейного программирования является оптимальное составление планов, распределение ресурсов, оптимизация производственных мощностей в сравнение с другими плановыми производствами при помощи математического анализа. Значимым компонентом в фактическом применении математических моделей составляет многозадачность, позволяющая данным методам применяться уже как в целевой функции, так еще и не для существующей.
В математическом прогнозировании ни в коем случае невозможно участие всех условий, оказывающих большое влияние на компетенцию системы. Более того, в реальных процессах способы модификации не могут оставаться неизменными. В редких случаях постоянными могут считаться коэффициенты переменных и лишь только в линейном и нелинейном программировании. В случае если прототип воспроизводит реальность в мельчайших подробностях, то при малейших изменениях модификациях характеристик, в лучшем случае у него должны быть неизменны те черты, которые характерны для поведения данного прототипа. Подобные концепции в дифференциальных уравнениях приобрели наименования «Грубых». Как известно в задачах линейного программирования не имеется постоянной связи с характеристиками системы, параметры меняются скачкообразно при изменении значений. Тем не менее, изменение решения может быть до такой степени огромно, что оно не будет содержать никакого физического смысла. [3]
В труде изучаются разрывы целевой функции, образующиеся при изменении характеристик. В качестве дополнения проанализируем модификации нефтепереработки и скоростного автотранспорта, в которых прогнозирование дает возможность приобрести значительных доход, либо, напротив, подсчитать недополучаемую выгоду в миллионы долларов.
Формирование скоростного автотранспорта в наш период времени является очень значимым вопросом, хотя разговоры идут только об использовании в кратчайшие сроки отдельных планов и финансовых расчетах о перспективе формирования скоростных путей. Железнодорожные пути по всей России требуют крупных муниципальных инвестиций, по этой причине актуальной остается цель построения верной математической модели расчета и способа их анализа для определения конкурентоспособности в сравнение с имеющими первенство самолетов и автомобилей.
В нефтяной сфере задачи линейного программирования обширно применяются для рационального планирования, распределения, производства и сбыта. Характерной чертой нынешней модели считается значительная размерность (применяется приблизительно 103 неустойчивых), что требует использования специализированных программ и разработки специальных критериев с целью установления корректности модели [2].
Для постановки задачи линейного программирования проанализируем проблему линейного программирования при помощи переменных 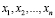 , которые приносили максимум целевой функции
, которые приносили максимум целевой функции 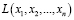 и удовлетворяли системе ограничений:
и удовлетворяли системе ограничений:
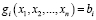 ,
, 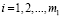 ,
,
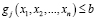 ,
,
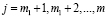 ,
,
где 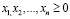 ,
, 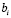 – константы
– константы 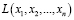 и
и 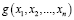 – линейные функции
– линейные функции
Функция меняется непрерывно при изменениях ее целевых характеристик, и лишь в угловых точках области допустимых значений ее производная может прерываться. Проанализируем проблему о воздействии лимитированных характеристик. Имеются определенные основные значения характеристик, присутствие которых существенно меняет конструкцию рационального решения, однако еще и совершает скачкообразные модификации максимума целевой функции. Подобные значения служат не только индикатором линейного программирования, но и отображают физическое и финансовое ограничения, которые требуют более тщательного математического анализа. В подобных ситуациях система перестает быть «Грубой».
С целью определения ключевых значений параметров в задачах линейного программирования, установим целевую функцию соответствующим способом:
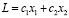 ,
,
где с1, с2 – маржинальная прибыль с учетом издержек на изготовление и перевозку единиц продукции х1, х2 соответственно [5].
Систему уравнений и ограничений запишем в виде:
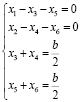
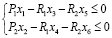 ,
,
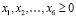 .
.
Здесь Р1, Р2, R1, R2, b – параметры задачи, которые упорядочены следующим образом b1 < b2, Р1< Р2, R1 <R2.
Изучим модель поведения целевой функции в максимальном значении
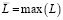
в зависимости от характеристик системы:
Установлено, что роль оптимальных значений 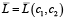 постоянна, вогнута или кусочно-постоянна. Проведем математический анализ решения в связи с характером ограничений. Проанализируем взаимосвязь
постоянна, вогнута или кусочно-постоянна. Проведем математический анализ решения в связи с характером ограничений. Проанализируем взаимосвязь 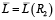 от параметров при фиксированном значении
от параметров при фиксированном значении 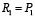 . При значениях
. При значениях 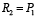 и
и 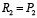 функция
функция 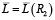
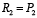 переносит прерывание 1-го рода. Аналогичным образом, имеются подобные значения характеристик в системе, небольшая трансформация которых может привести к разрыву первого рода целевой функции. Именно ключевые значения параметров системы линейного программирования при скачкообразном изменении максимума целевой функции приводят к банальным изменениям параметров. Система обретает концепцию не грубости и требует вспомогательных исследований корректности прогнозирования [4].
переносит прерывание 1-го рода. Аналогичным образом, имеются подобные значения характеристик в системе, небольшая трансформация которых может привести к разрыву первого рода целевой функции. Именно ключевые значения параметров системы линейного программирования при скачкообразном изменении максимума целевой функции приводят к банальным изменениям параметров. Система обретает концепцию не грубости и требует вспомогательных исследований корректности прогнозирования [4].
Объясним финансовую сущность проблемы на двух простых моделях.
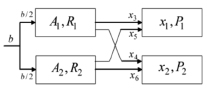
Необходимо максимизировать доход с авиа- и железнодорожных транспортировок пассажиров, установить число пассажиров в любом из типов транспорта и принять решение об эффективности одного из них в определенном регионе нашей страны. Пусть стоимость билетов на самолет составит Р1, а билетов в скоростной состав – Р2. Допустим, то что имеется 2 категории пассажиров А1 и А2, готовых заплатить за поездку стоимость R1 и R2. Число пассажиров в команде b/2. Доход с авиаперевозки одного пассажира – С1, скоростного поезда – С2. Количество пассажиров в самолете – Х1, в том числе из группы А1 – х3, из группы А2 – х5, в поезде пассажиров X2, в том числе из группы А1 – X4, из А2 – х6.
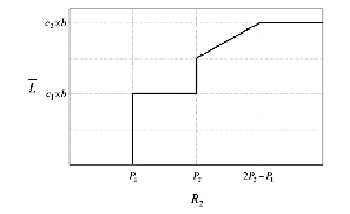
В случае если в группах низкий платежеспособный спрос и является меньше R2 < Р1, отсутствуют пассажиры на любой вид транспорта; при 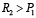 предпочтителен воздушный транспорт, при R2> Р2 используются оба вида; R2 > (2Р2 – Р1) – только высокоскоростные поезда.
предпочтителен воздушный транспорт, при R2> Р2 используются оба вида; R2 > (2Р2 – Р1) – только высокоскоростные поезда.
Таким образом, когда имеется платежеспособный спрос А2 такой, что R2>(2Р2–Р1) оказывается действенным на практике – скоростной автотранспорт, так как пассажиры эконом-класса имеют все шансы совместно с пассажирами бизнес-класса испытывать минимальные ограничения.
Таким образом, из пересмотренной модификации возможно совершить последующие заключения:
– улучшать скоростной автотранспорт имеет толк только лишь в том случае, когда имеется реальный спрос;
– при моделировании особое внимание надлежит отдать правильному определению основных характеристик с целью оценки финансовой эффективности.
При ключевых значениях параметров R1 = Р1 и R2 = Р2 целевая функция 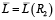 терпит разрыв. Данная организация утрачивает свойство грубости при малейшем изменении свойства материалов и обозначается изменением перечня материалов. Математическая модель, стремительно изменяет собственные действия при небольшом изменении характеристик, которые на физическом уровне никогда не могут измеряться конкретно, порождает при этом дополнительные научно-технические сведения.
терпит разрыв. Данная организация утрачивает свойство грубости при малейшем изменении свойства материалов и обозначается изменением перечня материалов. Математическая модель, стремительно изменяет собственные действия при небольшом изменении характеристик, которые на физическом уровне никогда не могут измеряться конкретно, порождает при этом дополнительные научно-технические сведения.
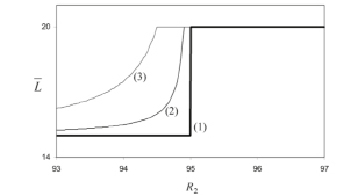
Пример численного поиска ключевых значений: отбор специальных значений характеристик в системе реальных моделей линейного программирования, обрисовываемых некоторыми тысячами уравнений, является затруднительным. К сожалению, задача осложняется еще и тем, что принятие решений в системах линейного программирования происходит лишь при конкретных параметрах. Однако в негрубых моделях можно провести диагностику численно, проводя вычисления около ограничений, за счет того, что она меняет свою манеру не только в определенной точке, но и около нее.
В данном случае, который описывается системой линейного программирования, изучены главные закономерности поведения рационального заключения задачи в зависимости от его характеристик. Показан главный смысл характеристик, в коих случаях происходит скачкообразная перемена функции и потребуется выполнить тест адекватности самой модели, направив свое внимание на правильность моделирования главных характеристик.
Как раз изучение поведения мотивированной функции в округи главных значений считается главным моментом максимизации маржинальной выгоды в вопросах рационального планирования. При данном тесте чувствительности рационального заключения к характеристикам мотивированной функции, оказывается наименьшее воздействие на итог и обязан проводиться во вторую очередь.

