Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Андреев И.В. 1

---

1 ФГБОУ ВО «Ставропольский государственный аграрный университет»

С использованием основных методов и понятий дискретной математики и математической логики проведены несколько типовых расчётов по корректности алгоритмов и процессов, написанных на языке программирования Pascal (структурированный и компилируемый язык программирования, является базой для многих других известных языков программирования), разобраны принцип и работа экспертной системы с использованием множеств и предикатов. С помощью логики высказываний описаны базовые алгоритмы решения и проверки задач, которые представлены перед программистом при проверке корректности программы и отдельных её частей, с использованием предикатов (функция с областью значений {0;1}, определенная n-й декартовой степени множества M) и составлении экспертной системы создана простая база данных (знаний) для получения информации из базы данных о британских королях и королевах и объяснены основные понятия математической логики и дискретной математики, которые применяются в ней.

Статья в формате PDF

0 KB

программирование

дискретная математика

теория множеств

экспертная система

1. Бондаренко В.А., Цыплакова О.Н., Родина Е.В Использование компьютерных математических систем в обучении математике // Информационные системы и технологии как фактор развития экономики региона: сб. научных статей по материалам Международной НПК. – Ставрополь: АГРУС Ставропольского ГАУ, 2013. – С. 46–50.

2. Долгих Е.В., Тынянко Н.Н. Теоретические экономико-математические модели // Современные проблемы развития экономики и социальной сферы: сборник материалов Международной научно-практической конференции, посвященной 75-летию Ставропольского государственного аграрного университета / Отв. редактор: Н.В. Кулиш, 2005. – С. 553–556.

3. Шелковой А.Н., Ююкин Н. А. Дискретная математика для экономистов, 2014.

4. Зепнова Н.Н., Кузьмин О.В. Применение методов дискретной математики при решении логических задач // Омский научный вестник. – 2014. – № 2 (130). – С. 14–17.

5. Попова С.В. Формирование алгоритмической культуры у студентов на занятиях по математике // Экономика регионов России: анализ современного состояния и перспективы развития: Сборник научных трудов по материалам ежегодной 68-й научно-практической конференции / Ответственный редактор Н.В. Кулиш, 2004. – C. 423–426.

6. Попова С.В., Колодяжная Т.А. Применение алгоритмов при обучении математике в вузе // Моделирование производственных процессов и развитие информационных систем / Даугавпилсский университет, Латвия, Европейский Союз Белорусский государственный университет, Беларусь Днепропетровский университет экономики и права, Украина Московский государственный университет им. М.В. Ломоносова, Россия, Санкт-Петербургский государственный политехнический университет Северо-Кавказский государственный технический университет Ставропольский государственный университет Ставропольский государственный аграрный университет. – Ставрополь, 2011. – С. 278–281.

7. Попова С.В., Смирнова Н.Б. Элементы алгоритмизации в процессе обучения математике в высшей школе // Современные проблемы развития экономики и социальной сферы: сборник материалов Международной научно-практической конференции, посвященной 75–летию Ставропольского государственного аграрного университета / Ответственный редактор: Н.В. Кулиш, 2005. – C. 526–531.

8. Смирнова Н.Б., Попова С.В. Основные принципы проектирования компьютерной математической модели // Сборник научных трудов по материалам Ежегодной 69-й научно-практической конференции, посвященной 75-летию СтГАУ / Ответственный редактор: Н.В. Кулиш, 2005. – С. 185–189.

9. Смирнова Н.Б., Попова С.В. Модели, подходы к классификации моделей // Экономика регионов России: анализ современного состояния и перспективы развития: сборник научных трудов по материалам Ежегодной 69-й научно-практической конференции, посвященной 75–летию СтГАУ / Ответственный редактор: Н.В. Кулиш, 2005. – С. 181–185.

10. Смирнова Н.Б., Попова С.В., Хачатурян Р.Е. Использование логической символики при обучении математике в вузе // Совершенствование информационных и коммуникационных технологий с целью активизации учебного процесса в вузе. – Ставрополь, 2006. – С. 191–195.

Дискретная математика и математическая логика – основа любого изучения информационных систем. В настоящий момент основы фундаментальной математической подготовки специалистов в области информатики, программирования и компьютерных наук описаны достаточно понятно: фундаментальные разделы математики, имеющие прикладную направленность на информатику, программирование и компьютеры, сосредоточены в курсах «Математическая логика», «Дискретная математика» и «Теория алгоритмов», являющиеся результатом алгоритмизации знаний, накопленных математикой [1, 3].

Бурное развитие дискретной математики обусловлено прогрессом компьютерной техники, необходимостью создания средств обработки и передачи информации, а также представления различных моделей на компьютерах, являющихся по своей природе конечными структурами. Большинство задач исследования операций (распределение ресурсов, сетевое планирование и управление, календарное планирование) описываются математическими моделями дискретного программирования [2, 9].

Умение логически понимать и решать задачу, которая будет поставлена перед любым программистом (независимо от языка программирования) является основополагающей, без логики невозможно полноценно и правильно решить задачу. Корректной можно считать только ту программу, которая исполняет функции, указанные в её технической спецификации, однако результат на уровне тестирования может кардинально отличаться в условиях реальной работы, поэтому необходимо проверить корректность алгоритма: нужно проверить изменения переменных программы, которые оно используется на всех этапах работы алгоритма (до, во время работы и после). Данные изменения будут рассматриваться как предикаты.

Пусть P – предикат, верный для входных значений алгоритма A, а Q – предикат, содержащий условия, которые удовлетворяют выходные значения. Высказывание 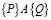означает следующее: «если алгоритм A начинается с корректного значения P, то она закончится при истинном значении Q». Предикат P называется предусловием, Q – постусловием. Высказывание 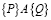тоже предикат, поэтому доказательство алгоритма A равносильно доказательству верности 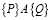. Основываясь на этом, можно доказать правильность алгоритма «Квадратный многочлен» на языке Pascal:

Текст программы:

{x – вещественное число}

Begin

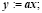
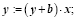
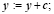End

Поделим алгоритм на части и зафиксируем обозначения пред- и постусловий.

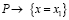
begin

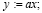
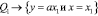
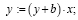
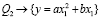
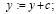
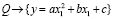
Подстановки показывают, что высказывания:

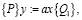
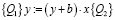
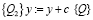
верны.

Таким образом, предикат

{Q} Квадратный многочлен {P}

верен. Таким образом, алгоритм «Квадратный многочлен» корректен.

Алгоритм условных высказываний тоже поддается такому доказательству, необходимо только отразить альтернативные пути в алгоритме [6].

Предположим, что высказывание

if условие then

высказывание 1;

else

высказывание 2;

вводит предусловие P и в конце даёт условие Q. Поэтому необходимо доказать истинность двух предикатов:

{P и условие} высказывание 1 {Q}

и {P и не (условие)} высказывание 2 {Q}.

Теория множеств используется для наиболее удобного описания массы концепций в информатике. Одним из примеров применения теории множества в программировании является база данных. Возьмём за пример экспертную систему [10].

Экспертная система создаётся с целью подмены собой специалистов в данной области. Реализуется это благодаря накоплению базы знаний известных событий с определением набора правил вывода, из-за чего ответы на запросы могут быть выведены логическим путём из базы знаний.

Создадим экспертную систему под названием «Королевская династия Англии». Для начала подготовим список фактов, используя предикаты «родитель» и «жена».

Родитель (Георг I, Георг II) жена (София, Георг I)

Родитель (Георг III, Георг IV) жена (Вильгельмина, Георг II)

Родитель (Георг III, Вильгельм IV) жена (Шарлотта, Георг III)

Родитель (Георг III, Эдвард) жена (Каролина, Георг IV)

Родитель (Эдвард, Виктория) жена (Аделаида, Вильгельм IV)

Родитель (Виктория, Эдвард VII) жена (Виктория, Альберт)

Родитель (Эдвард VII, Георг V) жена (Александра, Эдвард VII)

Родитель (Георг V, Эдвард VIII) жена (Виктория Мари, Георг V)

Родитель (Георг V, Георг VI) жена (Елизавета, Георг VI)

Родитель (Георг V, Елизавета II) жена (Елизавета II, Филипп)

Родитель (Виктория, Элис)

Родитель (Элис, Виктория Альберта)

Родитель (Виктория Альберта, Филипп)

Родитель (x, y) означает, что x является родителем y, а жена (x, y) означает, что x – жена y. Это стандартное чтение предикатов, используемых языками программирования, как, например, PROLOG [4].

Для извлечения информации необходимо отправлять запросы в базу данных. Пример: «является ли Георг I отцом Георга III», то ответ будет отрицательным, поскольку предикат родитель (Георг I, Георг III) не существует в списке. Формат запроса зависит от языка программирования, который поддерживает та или иная база данных. Таким образом, использование баз данных в работе помогает упорядочить информацию и наиболее эффективно работать с ней. Запросы формируются по принципу: «? – предикат». При этом подразумевается наличие переменной в предикате, которое будет равносильно вопросу о существовании того или иного элемента [7].

Сформулируем правило вывода для получения информации о матерях из системы. Необходимо обозначить правило мать(x) так, чтобы положительный ответ на этот запрос формировался только в том случае, если x – жена чьего-то родителя или x – женщина и родитель. Правило такого вывода определяется таким образом:

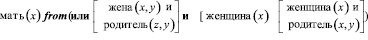
Но данное правило вывода не найдёт всех матерей из-за того, что база данных не полная – в ней не записаны, например, дети Елизаветы Второй. Полученный результат показывает трудности, возникающие при попытках ограничения реального мира рамками математической модели [5, 8].

Библиографическая ссылка