Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Даутова Р.Р. 1

---

1 Финансовый университет при Правительстве Российской Федерации

В данной работе выполнено эконометрическое моделирование стоимости квартир на вторичном рынке недвижимости в Красногорском районе Московской области в 2016 году. Показан процесс отбора факторов, оказывающих влияние на стоимость квартир, выполнено построение модели, отражающей влияние изменения отобранных факторов, а именно: тип дома, наличие балкона и телефона. Проведен анализ полученной модели. Модель признана адекватной и значимой. Полученная модель позволяет сделать выводы об изменении стоимости квартиры на вторичном рынке недвижимости в Красногорском районе под влиянием различных факторов, которую можно использовать для прогнозирования. Кроме того, рассчитана доля влияния каждого фактора в суммарном влиянии всех факторов для определения фактора, оказывающего наибольшее влияние на формирование стоимости квартиры в Красногорском районе.

Статья в формате PDF

0 KB

моделирование стоимости квартир

параметры формирования стоимости квартир

корреляция

регрессия

1. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: учеб. Пособие. – 3–е изд. – М.: Вузовский учебник: ИНФРА-М, 2013. – 389 с.

2. Орлова И.В., Филонова Е.С., Агеев А.В. Эконометрика: Компьютерный практикум для студентов третьего курса, обучающихся по специальностям 080105.65 «Финансы и кредит», 080109.65 «Бухгалтерский учет, анализ и аудит». – М., 2011.

3. Данные компании риэлтерской компании «Гларекс Норд Вест» (Glarex Nord West) [Электронный ресурс] // URL: http://nord-west.biz/ (дата обращения: 10.11.16).

4. Данные компании ООО «Красногорская Городская Служба Недвижимости» [Электронный ресурс]. – URL: http://www.kgsn.su/ (дата обращения: 10.11.16).

5. Данные компании «Планета Недвижимость» [Электронный ресурс] // URL: http://www.land25.ru/ (дата обращения: 10.11.16).

6. Федеральная служба государственной статистики [Электронный ресурс] // URL: http://www.gks.ru/dbscripts/munst/munst46/DBInet.cgipl=8006001/ (дата обращения: 10.11.16).

В данной работе выполнено эконометрическое моделирование стоимости квартир на вторичном рынке недвижимости в Красногорском районе Московской области.

Цены на вторичном рынке снижаются уже несколько кварталов подряд, однако в последние месяцы 2016 г. темпы падения стали замедляться. Сложная экономическая обстановка в стране вынуждает граждан больше экономить, что приводит к снижению спроса и уменьшению средней стоимости 1 кв. м.

Корректная оценка стоимости недвижимости обеспечивает условие для стабильного развития национальной экономики. Таким образом, моделирование стоимости квартир объясняет актуальность данной темы.

В качестве рассмотренного рынка выступает вторичный рынок. Красногорский район входит в Московскую область. Общая площадь района составляет 224,99 км2 [6], численность населения – более 217 404 человек [6].

Цель данной работы – определить модель, описывающую рынок вторичного жилья Московской области в Красногорском районе, определить факторы, влияющие на стоимость квартиры и степень их влияния.

Данные для анализа взяты с сайтов Риэлторской компаний «Гларекс Норд Вест» (Glarex Nord West) [3], ООО «Красногорская Городская Служба Недвижимости» [4] и «Планета Недвижимость» [5] на ноябрь 2016 года.

Факторами, оказывающими влияние на стоимость квартир, являются: общая площадь квартиры, тип дома, этажность, тип санузла, наличие балкона, лифта, телефона в квартире.

Помимо этого, было произведено введение фиктивных переменных:

• тип дома панельный – «0», кирпичный – «1»;

• первый и последний этаж – «1», все остальные этажи – «0»;

• санузел смешанный – «1», раздельный – «0»;

• наличие балкона – «1», отсутствие – «0».

• наличие лифта– «1», отсутствие – «0».

• наличие телефона – «1», отсутствие – «0».

Всего выбрано 70 наблюдений.

Для того, чтобы определить корреляционную зависимость между стоимостью квартиры (Y) и имеющимися переменными, оказывающими на неё влияние(Xj), необходимо построить матрицу коэффициентов парной корреляции между всеми имеющимися переменными (табл. 1).

Таблица 1

Матрица коэффициентов парной корреляции между всеми переменными

Из данной таблицы можно сделать следующие выводы:

• цены на квартиры ниже в панельных домах (т.к. наблюдается прямая корреляционная зависимость между переменными Y и X2);

• цены на квартиры с наличием телефона выше (т.к. между переменными Y и X7 наблюдается прямая корреляционная зависимость);

• цены на квартиры выше в среднем на остальных этажах (поскольку между переменными Y и X3 наблюдается обратная корреляционная зависимость).

Корреляционная зависимость между остальными переменными слабая.

Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t-критерия Стьюдента [1].

Рассчитанные значения t-критерия Стьюдента в дальнейшем сравниваются с критическим значением tкр. при уровне значимости α = 0,05 и числе степеней свободы k = n – 2 = 70 – 2 = 68. Следовательно, tкрит. = 0,471.

При tрасч > tтабл, полученные значения коэффициентов корреляции значимы. Таким образом, наиболее тесная и значимая зависимость наблюдается между стоимостью квартиры Y и жилой площадью квартиры Х2 (tрасч=8,23).

Качество модели можно определить с помощью R-квадрат – доля объясненной дисперсии. R-квадрат равен квадрату корреляции между предсказанными и наблюдаемыми значениями Y [1, 2].

Таким образом, коэффициент детерминации в выбранной модели = 0,596, показывает, что 59,6 % вариации цены квартиры объясняется вариацией факторов, включенных в модель.

Проверка переменных на мультиколлинеарность производится с помощью построения матрицы парных корреляций (табл. 2).

Таблица 2

Проверка переменных на мультиколлинеарность

Из данной таблицы видно, что коэффициенты парной корреляции между переменными меньше 0,8, значит явление мультиколлинеарности не установлено.

Для построения модели стоимости квартир на вторичном рынке недвижимости в Красногорском районе изначально следует исключить параметры, оказывающие незначительное влияние. Необходимо пошагово исключать параметры с использованием протокола регрессионного анализа [1, 2]. Создается протокол выполнения регрессионного анализа для всех исследуемых параметров (табл. 3).

Таблица 3

Фрагмент протокола регрессионного анализа для всех параметров

Из данного протокола видно, что наименьшее влияние на стоимость квартир оказывает тип санузла в квартире. Значение t-статистики этого параметра меньше tкр, кроме того, нижние и верхние границы 95 % доверительных интервалов проходят через 0. Из дальнейших расчетов следует исключить параметр X4.

Далее проводится оценка значимости оставшихся коэффициентов. Каждый раз составляется новый протокол регрессионного анализа для оставшихся исследуемых параметров [1, 2]. Таким образом, исключается параметр этажности (X3), затем параметр наличия лифта (Х6) и параметр общей площади (Х1). Далее необходимо создать новый протокол регрессионного анализа для оставшихся параметров (табл. 4).

Таблица 4

Фрагмент протокола регрессионного анализа для Х2, Х5, Х7

Ни один из показателей не проходит через 0. Значения t-статистики всех показателей больше чем tкрит. Значит, все оставшиеся показатели являются значимыми. Следовательно, тип дома, наличие балкона и телефона являются параметрами, оказывающими влияние на формирование стоимости квартиры.

Полученная модель выглядит следующим образом:

Y=3338735+1224305X2+386964,8X5+ +629361,1X7.

Для оценки значимости полученной модели следует рассчитать значение F-критерия Фишера [1]. Расчетное значение F-критерия Фишера для полученной модели составляет 49,37. Данное значение необходимо сравнить с табличным значением F-критерия, который можно найти с помощью функции РАСПОБР в Excel, где количество степеней свободы равно v1 = k = 2, v2 = n–k–1 = 70–2–1 = 67. Табличное значение F-критерия составляет 3,13. Поскольку Fрасч>Fтабл, уравнение регрессии следует признать значимым, то есть его можно использовать для анализа и прогнозирования.

Для оценки точности модели необходимо проанализировать фрагмент протокола выполнения регрессионного анализа в части остатков и посчитать относительные погрешности по формуле [1]:

.

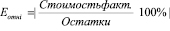Средняя относительная погрешность модели составляет 13,82 %, что меньше критической погрешности равной 15 %. Следовательно, точность модели является удовлетворительной.

Оценить вклад каждого из факторов в вариацию можно с помощью дельта-коэффициентов. Для каждого коэффициента регрессии следует вычислить коэффициент эластичности по формуле [1]:

.

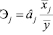Для полученной модели коэффициенты эластичности получаются следующие: Э2 =0,08; Э5 =0,07; Э7 =0,05.

Коэффициент эластичности Э2 показывает на сколько процентов в среднем изменится стоимость квартиры при изменении типа дома, Э5 – при наличии балкона, Э7 – при наличии телефона.

Также необходимо вычислить бетта-коэффициент по следующей формуле [1]:

.

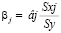В данном случае, бетта-коэффициенты принимают следующие значения: β2 = 0,51; b5 = 0,16; b7 = 0,28.

Бета-коэффициент показывает, что при изменении типа дома, стоимость квартиры увеличится на 548375,2 руб; при изменении наличия балкона в квартире, стоимость кв. увеличится на 176075,1 руб; при изменении наличия телефона, стоимость квартиры увеличится на 303740,4 руб.

Кроме того, необходимо рассчитать дельта коэффициенты по формуле [1]:

Δj = ry,xj βj / R2.

Для модели дельта коэффициенты получаются следующие: Δ2 = 0,61, Δ5 = 0,08, Δ7 = 0,31.

Дельта коэффициенты показывают долю влияния каждого фактора в суммарном влиянии всех факторов. Из чего можно сделать вывод, что на стоимость квартиры наибольшее влияние оказывает тип дома (Х2).

Итак, в процессе исследования была построена модель на основе эконометрического анализа, позволяющая сделать выводы об изменении стоимости квартиры на вторичном рынке недвижимости в Красногорском районе под влиянием различных факторов, которую можно использовать для прогнозирования.

Библиографическая ссылка