Когда исследователи анализируют процессы, касающиеся моделирования рассеяния электромагнитных волн на разных объектах, имеющих сложную форму, им приходится решать задачи, которые связаны с радиолокационным распознаванием, формированием условий, для которых происходит соблюдение электромагнитной совместимости.
Разные ученые определили модели (являющимися, в том числе и аналитическими), при появлении них появились возможности того, чтобы осуществлять оценки характеристик рассеяния электромагнитных волн для большого класса объектов [3, 4].
В некоторых задачах возникает необходимость того, чтобы обладать информацией не об угловых зависимостях по характеристикам рассеяния, а о средних значениях характеристик рассеяния в определенных секторах углов наблюдения. После анализа различных литературных источников можно привести данные относительно средних значений ЭПР (эффективные площади рассеяния), которые рассчитываются для объектов, характеризующихся простыми формами (плоские поверхности, шары, эллипсоиды и т.д.). Для тех случаев, когда объекты, подлежащие исследованию, имеют сложную форму, требуется привлекать численные методы. Среди объектов разработок можно отметить полые структуры, которые имеют сложные формы, входящие в состав различных антенных систем и систем дифракционных структур. Величины мощностей, относящихся к вторичному рассеянию подобных объектов могут быть довольно большими [6, 7].
В рамках классического метода решения уравнения Гельмгольца, в котором применяется подход, связанный с разделением переменных, получаются аналитические результаты лишь для таких неоднородностей, поверхности которых будут совпадать с координатными поверхностями в ортогональных системах координат, по которым происходит разделение уравнения Гельмгольца.
Способы, для того, чтобы проводить вычисление рассеянных полей комплексных объектов для разных областей наблюдения являются известными.
Для интегральных уравнений второго рода, в случае их практического использования, можно указать большое число достоинств, так, например, указывают то, что решение будет устойчивым с точки зрения малых возмущений в исходных параметрах проблем.
При этом особенности численных решений в интегральных уравнениях, которые традиционным образом решаются на базе проекционных подходов, имеют некоторую связь с тем, каким образом осуществляется выбор систем базисных функций, позволяющих обеспечить повышение эффективности вычислительных операций по отношению к скоростям сходимости, параметров, определяющих производительность процессоров и объемов оперативной памяти вычислительных устройств.
Когда используется метод конечных элементов в областях, в которых осуществляется процесс поиска решения в системах дифференциальных уравнений, идет определение конечного числа подобластей.
По каждой из подобных подобластей требуется провести выбор типа аппроксимирующих функций. среди простейших вариантов можно указать линейную зависимость, при этом анализируют полиномы, имеющие 1 степень.
Значение аппроксимирующей функции вне подобласти мы полагаем равным нулю. Необходимо проводить стыковку значений функций относительно границ подобластей.
Процесс поиска коэффициентов в аппроксимирующих функциях идет исхлдя из условий того, что будет равенство значений по соседним функциям по границам между подобластей.
Затем подобные коэффициенты необходимо выражать как зависящие от значений функций по соответствующим узлам подобластей. Идет формирование системы линейных алгебраических уравнений.
Количество уравнений будет равно количеству неизвестных значений, которые относятся к узлам, по ним мы ведем поиск решения анализируемой системы. Это количество будет прямо пропорционально числу подобластей и ограничения по расчетам определяются только тем, какие возможности в конкретном компьютере.
В связи с тем, что для каждой из подобластей есть связь с некоторым числом соседних, тогда в системе линейных алгебраических уравнений характерным будет то, что она будет разряженной, это существенным образом определяет упрощение процедуры для ее решения.
Но не всегда является возможным определить точные и аналитические решения по распределению токов, но могут быть случаи, в которых можно указать приближение по фактическому распределению токов на объектах.
Кроме весьма простых систем, проведение электромагнитного анализа требуется для того, чтобы оценивать электрические характеристики и осуществлять проектирование в высокопроизводительных телекоммуникационных и информационных системах, это во многих случаях определяет большие значения чисел степеней свободы, и в этой связи появляются трудности при численном решении задач.
Поэтому, при решении масштабных проблем, в основном нельзя использовать многие классические численные алгоритмы вследствие вычислительных трудностей и больших требований к памяти. Помимо этого мы можем увидеть и неадекватность аппроксимационных моделей, которые используют в таких подходах.
Для того, чтобы моделировать сложные, крупномасштабные электромагнитные проблемы, важно стремиться к тому, чтобы уменьшать сложность используемых методик.
В последнее время были осуществлены исследования по нескольким сложным быстрым численным подходам на разных шагах формирования методик радио расчетов, в том числе и при формулировке математических задач, использовании методов конечных трехмерных проекций и решении дискретных проблем, например: проведении оценок на базе быстрого метода мультиполей, применение метода быстрого преобразования Фурье и др.
В случае объектов, имеющих большие размеры метод моментов в классическом его использовании и введении пробных функций определяет возникновение больших и сильно заполненных матричных уравнений, устранить проблемы при этом довольно сложно.
Целью настоящей работы является проведение исследований, связанных с оценкой возможностей использования способа оптимизации, который дает возможности для построения полых структур, имеющих максимальные значения характеристик рассеяния для заданных углов.
Нами решались такие основные задачи:
1. Проведение анализа по тому, какая структура подсистемы анализа полых структур, характеризующимися сложной формой.
2. Проведение анализа по моделям расчетов характеристик рассеяния полых структур, имеющих максимальные характеристики рассеяния, исходя из того, что проводилась комбинация метода интегральных уравнений и метода оптимизации, базирующегося на генетическом алгоритме [5].
3. Подведение выводов о том, насколько целесообразен предлагаемый подход.
На рис. 1 приведена геометрия исследуемой полой структуры.
На основе машинных экспериментов возникают возможности формирования заключения о том, насколько результаты, которые возникают при моделировании, мы можем рассматривать как достоверные и надежные. Исходя из того, что есть ограничения, связанные с лабораторным пространством, при изготовлении моделей сложных объектов, могут потребоваться привлечение больших средств, сами эксперименты будут довольно дорогие [8, 10]. Учитывая вышесказанное, применяют компьютерное моделирование с привлечением систем автоматизированного проектирования (САПР) [3, 4].
Мы предложили структуру подсистемы анализа полых структур, имеющих сложную форму (рис. 2).
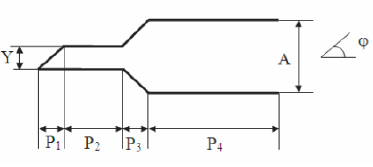
Рис. 1. Схема рассеяния электромагнитной волны на полой структуре сложной формы
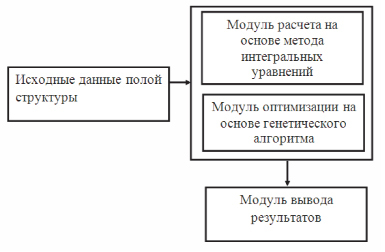
Рис. 2. Структура подсистемы анализа полых структур, имеющих сложную форму
Плотности токов, относящиеся к поверхностям исследуемого объекта можно рассчитать, основываясь на уравнении Фредгольма первого рода, в которое входит плотность искомого электрического тока при Е-поляризованной радиоволне [4, 7]:
,
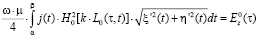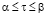, (1)
где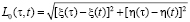 
– является расстоянием между точкой наблюдения и точкой интегрирования, 
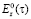– является продольной составляющей напряженности электрического поля, которая рассматривается в точке на контуре. Происходит задание контура структуры на основе параметрической формы:
,
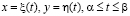а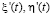 
– являются первыми производными по соответствующим функциям, 
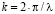, λ – длина падающей радиоволны.
При решении уравнения (1) методом моментов оно дискретизуется и приводится к системе линейных алгебраических уравнений, из которой определяются продольные электрические токи с плотностью
, 
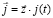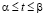, (2)
Двумерная ЭПР полой структуры определяется на основе выражения
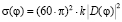, (3)
здесь
,
.
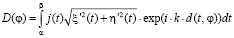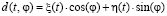Было проведено моделирование рассеяния электромагнитных волн на полой структуре сложной формы для следующих параметров: 4l≤A≤7l, 2l≤ P1≤3l, 3l≤ P2≤4l, 2l ≤ P3≤ 3l, 5l≤ P4≤6l, 2l≤Y≤3l.
На основе использования комбинации метода интегральных уравнений и метода оптимизации было установлено, что максимальное значение эффективной площади рассеяния для угла наблюдения j=30° достигается для значений параметров: A=6.5l, P1=2.7l, P2=3.4l, P3=2.7l, P4=5.9l, Y=2.67l, максимальное значение эффективной площади рассеяния для угла наблюдения j=37° достигается для значений параметров: A=6.2l, P1=2.3l, P2=3.1l, P3=2.3l, P4=5.7l, Y=2.3l.
Библиографическая ссылка
Требунских И.С. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАССЕЯНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН НА ПОЛЫХ СТРУКТУРАХ // Международный студенческий научный вестник. – 2017. – № 4-8. ;URL: https://eduherald.ru/ru/article/view?id=17676 (дата обращения: 21.11.2024).