В качестве особого вида задач в электродинамике можно отметить такие, в которых проводится анализ закономерностей рассеяния радиоволн на металлических структурах, характеризующимися различными формами, они являются компонентами технических объектов (элементами конструкций) или антенно-фидерных устройств [3, 4]. Осуществление расчетов характеристик электромагнитных полей по разным электродинамическим устройствам происходит с привлечением большого числа соответствующих методов [6, 7]. При этом представляет интерес создание таких алгоритмов, которые дают возможности для расчетов рассеивающих характеристик объектов, которые имеют размеры, лежащие в резонансном диапазоне [6-8].
Объекты, которые рассеивают электромагнитные сигналы (радиолокационные компоненты (РК) в космическом, воздушном, наземном и водном размещении) и составляющие, связанные с преобразованием энергии радиоеволн (рассматривают, например, применение транспарантов, средств для поглощения радиоизлучений в радиодиапазоне волн, антенных устройства в СВЧ и КВЧ диапазонах), во многих случаях, могут быть охарактеризованы заметными электрическими размерами (ЭР), комплексной геометрией, использованием поглощающих и нелинейных составляющих. Проведение анализа и синтеза таких электродинамических составляющих в рамках грубых подходов и представлений о закономерностях существующих в них физических процессах определяет вероятность того, что будут возникать существенные и трудно контролируемые погрешности по оценке их базовых характеристик, они во многих случаях, весьма быстрым образом изменяются, когда изменяется частота, вид поляризации и угол падения радиоволны. То, что измеряются основные характеристики РК (рассматривают поляризационную матрицу, эффективную поверхность рассеяния по моностатическим и бистатическим режимам рассеяния) для широкой полосы частот и обширного углового сектора, определяет необходимость или в аттестованных специально оборудованных антенных полигонах, или применяют аттестованную безэховую камеру (стоимость ее может быть несколько миллионов долларов), при этом можно столкнуться с большими затратами: временные и материальные средства.
Анализируемые методы есть возможность условным образом поделить по трем классам.
В первом – идет рассмотрение асимптотических методов. В них также можно сделать определение двух групп: асимптотических и эвристических. Различие состоит в том, какое математическое обоснование. Среди первых – более обоснованных – можно отметить подходы в геометрической оптике, геометрическую теории дифракции, среди вторых – подходы в физической оптике (ее называют по-другому как приближение Кирхгофа) и метод краевых волн П.Я. Уфимцева.
Во втором классе существуют строгие методы. Такими можно считать методы, на базе которых можно получать решение, которое будет сколь угодно близко к точному. Среди этих методов рассматривают использование: метода разделения переменных, метода интегральных преобразований, метода интегральных уравнений.
В третьем классе выделяют гибридные методы. В основном, в рамках подобного подхода на основе приближенного способа идет определение точек (или полей), которые потом следует подставить в разные электродинамические операторы (происходит уточнение на их основе). В качестве примера подобных методов можно указать метод стационарного функционала Ю. Швингера, разные комплексные методы, в которые входит множество методов и др. [2].
Для квазистатических областей решение задач можно получить, исходя из того, как решается волновое уравнение (уравнения Гельмгольца), но при этом аналитический вид решения достигается не во всех случаях и приходится использовать численное решение.
Для резонансных областей (которые считаются наиболее трудными в исследованиях) большей частью применяют подходы, связанные с методом разделения переменных или методом интегральных уравнений.
Для квазиоптических областей могут применяться два вида методов: лучевые и волноводные. Лучевые методы, характеризуются геометрической оптикой и ее разновидности: рассматривают геометрическую теорию дифракции, которая дает возможности для распространения геометрических методов на дифракционные проблемы; комплексную геометрическую оптику, позволяющую проводить вычисление полей для областей рефракционной тени, метод параболических уравнений, что позволяет расширить сферу использования лучевых методов.
В волновые методы входит метод физической оптики (имеется ввиду приближение Кирхгофа) при уточнениях, среди них укажем метод краевых волн, он дает возможности определить поправки для полей излучения, которые касаются построения приближенных (квазиоптических) собственных функций.
На основе формулировки задачи с помощью интегрального уравнения или систем интегральных уравнений, можно обеспечить снижение размерности проблемы и еще исходные граничные задачи для неограниченных областей будут сведены к задачам для ограниченных областей (на поверхностях или в объемах рассеивателей). Относительно такого подхода токи, которые есть на поверхности тел, могут быть определены на базе решений интегральных уравнений. Проведение расчета рассеянных электромагнитных полей идет исходя из найденных токов. Такой подход эффективно применяется для того, чтобы рассчитывать характеристики рассеяния тел, размеры их относятся к резонансным областям (говорят о двумерных задачах), и тел, имеющих размеры, лежащих в пределах нескольких длин волн (говорят о трехмерных задачах). При том, что растут размеры тел резким образом идет увеличение необходимого для проведения расчетов машинного времени, объемов оперативной памяти. На базе метода можно делать расчеты характеристик рассеяния по идеально проводящим объектам с радиопоглощающими покрытиями.
При разработке алгоритмов можно столкнуться с проблемами, определяющими необходимость получения данных по тому, какие закономерности определяют связь средних характеристик рассеяния и размеров электродинамических объектов [2, 10].
Мы проводили анализ на основе двумерной модели. Анализ литературных источников показывает, что двумерные модели в ряде случаев могут быть рассмотрены при проведении расчетов рассеивающих характеристик объектов, имеющих прямоугольную форму.
На рис. 1 приведена иллюстрация рассматриваемой нами задачи. Размер объекта для одного направления W, для другого направления S. Проводим вычисление общей длины контура для всего объекта. Характерным размером мы будем считать определенную величину R для контура J. Требуется, чтобы была найдена связь между R и J, значения которых определяют экстремальные значения средних эффективных площадей рассеяния (ЭПР) по некоторым секторам углов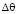 
. Отсчет углов 
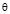происходит по часовой стрелке.
Есть соответствие углов наблюдения областям передних полусфер, существуют ограничения по следующим значениям: 5° ≤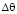
≤ 55°. Рассеянные характеристики рассчитывались на базе метода интегральных уравнений [1, 7]. Был использован строгий метод так как:
1) Изменение размеров объектов происходило в весьма большом диапазоне, в том числе была рассмотрена и низкочастотная область;
2) Базируясь на приближенных аналитических подходах, мы можем воспользоваться возможностями для того, того, чтобы получить приемлемые оценки только по значениям ЭПР, которые относятся к областям в локальных максимумах для диаграмм обратного рассеяния. Для областей минимумов в диаграммах обратного рассеяния значения ошибок могут доходить до десятков дБ.
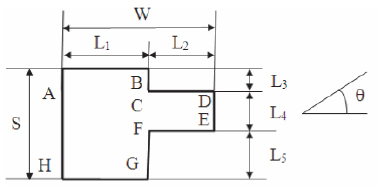
Рис. 1. Схема рассеяния радиоволны на объекте сложной формы
Мы рассматривали уравнение Фредгольма первого рода, на основе которого задается связь плотности электрического тока для случая Е-поляризации.
Задачу, направленную на то, чтобы определить R и J, дающих максимальные значения средней ЭПР, решаем следующим образом.
1. Проводится задание сектора углов наблюдения Δθ.
2. Ведется формирование целевой функции. Происходит варьирование значений для областей изменения R и J.
3. Проводится аппроксимация зависимостей R от J, при этом используется метод наименьших квадратов [5].
В тех случаях, когда объекты могут быть представлены в виде совокупности N невзаимодействующих компонентов, проводить расчет их ЭПР следует с привлечением метода суперпозиции.
Приведем пример решения задачи для следующих размеров объекта: 0≤L1?2.1l,0≤ L2≤1.7l, 0≤L3≤1.9l, 0≤L4≤2.2l, 0≤L5≤2.4l, то есть W=3.8l, S=6.5l. В качестве характерного участка на контуре был выбран участок ABCD.
На рис. 2 дана зависимость J(R) (кривая 1), проведена аппроксимация этой зависимости на основе метода наименьших квадратов (кривая 2), значение степени полинома составило 5.
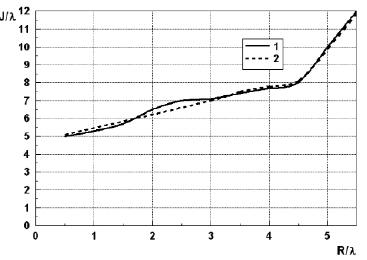
Рис. 2. Зависимость контура J от длины участка контура R, дающая максимальное значение эффективной площади рассеяния
Средняя ЭПР может быть определена таким образом
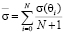, (1)
где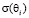 
– является величиной ЭПР при угле наблюдения 
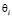; N – является общим числом углов, для которых происходит наблюдение.
ЭПР объекта, который состоит из N невзаимодействующих отражателей, определяется на основе рассмотрения значений ЭПР по каждому простейшему отражателю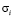 
и при учете разности фаз радиоволн, которые идут от разных отражателей [9]:
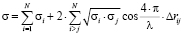, (2)
где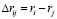 
, 
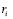является расстоянием от центра i-го отражающего элемента до точки приемника.
Тогда из (2) мы можем получить такое выражение для максимальной средней ЭПР объекта:
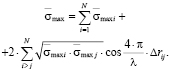(3)
Библиографическая ссылка
Требунских И.С. МОДЕЛИРОВАНИЕ РАССЕЯНИЯ РАДИОВОЛН НА ИДЕАЛЬНО ПРОВОДЯЩИХ ТЕЛАХ // Международный студенческий научный вестник. – 2017. – № 4-8. ;URL: https://eduherald.ru/ru/article/view?id=17675 (дата обращения: 23.11.2024).