Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дюмаева О.В. 1 Бершадская Е.Г. 1

---

1 Пензенский государственный технологический университет

В статье рассматривается подход к построению модели планирования для диспетчерских служб транспортных компаний, основанный на статистическом анализе потоков пассажиров. Исследование проводится на модели как системе массового обслуживания с учетом всех ограничений в рассматриваемой предметной области. В управлении общественным транспортом широко используются информационно-управляющие системы, обеспечивающие эффективность его функционирования. С точки зрения теории, общественный транспорт традиционно рассматривают, как систему массового обслуживания, где заявки формируются потоками пассажиров, а исполнительными элементами или обработчиками, являются транспортные единицы. В реальном мире за пассажиров идет конкурентная борьба между несколькими компаниями, предлагающими различные условия перевозок. Статическое планирование не может обеспечить реакцию на динамические изменения характеристик потоков пассажиров и состояния транспортных магистралей. Низкая эффективность работы программно-аппаратных комплексов управления ТС может быть связана с тем, что они не учитывают конкуренцию на рынке транспортных услуг. Для решения этой проблемы необходимо ввести новые оценки качества алгоритмов управления, в частности их способность оптимизировать работу объекта управления при воздействии на него конкурирующих субъектов.

Статья в формате PDF

0 KB

транспортные системы

система массового обслуживания

поток пассажиров

загрузка

1. Бершадская Е.Г., Бурукина И.П., Акимов А.А. Информационная система поддержки учебной и научной деятельности кафедры // Современные информационные технологии. – 2012. – № 15. – С. 98–101.

2. Лупин С.А, Тан Шейн, Чжо Чжо Лин. Особенности моделирования транспортных систем в условиях конкуренции // Информационные системы и технологии. – 2013. – №3(77). – С. 45–53.

3. Тан Шейн. Влияние конкуренции на эффективность систем управления общественным транспортом // XV Международная телекоммуникационная конференция молодых ученых и студентов «Молодежь и наука»: Тезисы докладов. В 3-х ч. Ч. 3. – М.: НИЯУ МИФИ, 2012. – 204 с., C. 124–126.

4. Тан Шейн. Структура модели транспортной системы. //Микроэлектроника и информатика – 2010. 17–я Всероссийская межвузовская научно-техническая конференция студентов и аспирантов: Тезисы докладов. – М.: МИЭТ, 2010. – 352 с. С. 219.

5. Kachurina P., Vidiasova L.B., Trutnev D., Buccafurri F., Bershadskaya E. Biometric identification in ehealthcare: learning from the cases of Russia and Italy // Lecture Notes in Computer Science. – 2015. – Т. 9265. – С. 103–116.

Одной из отличительных черт современной эпохи, без сомнения, можно считать широкое использование вычислительных систем практически во всех окружающих нас областях. Одной из таких областей, в которых сейчас происходит активное внедрение современных технологий управления, является транспорт.

В управлении общественным транспортом широко используются информационно-управляющие системы, обеспечивающие эффективность его функционирования. С точки зрения теории, общественный транспорт традиционно рассматривают, как систему массового обслуживания, где заявки формируются потоками пассажиров, а исполнительными элементами или обработчиками, являются транспортные единицы [4]. Система управления в зависимости от интенсивности потока заявок формирует необходимое количество обработчиков и их вместимость, рассчитывает интервал движения. Заметим, что именно соблюдение интервала движения является важнейшей целевой функцией диспетчерских систем управления. Такой подход вполне применим для управления системами, в которых нет необходимости учитывать экономические параметры, например, при планировании работы внутризаводского транспорта [3]. Но кроме удовлетворения запросов пассажиров, транспортные системы должны обеспечивать и рентабельность перевозок. Следование заданным интервалам движения при уменьшении потока пассажиров, очевидно, приведет к финансовым издержкам и сделает перевозки нерентабельными. Необходимо искать иные методы управления, способные гибко реагировать на изменение нагрузки.

В подавляющем большинстве случаев диспетчерские системы на транспорте используют статические модели планирования, основанные на статистическом анализе потоков пассажиров.

Пусть интенсивность потока пассажиров определяется функцией P(t). Тогда количество пассажиров, появившихся за время 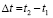и претендующих на обслуживание, можно определить как:

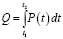. (1)

Первый подход основан на доминировании интересов перевозчиков. Если допустить, что вместимость C (Capacity) всех транспортных средств одинакова, то нахождение интервала их движения h (headway) может сведено к решению следующего уравнения:

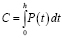. (2)

В случае равномерного распределения потока пассажиров P(t) = λ получаем:

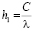. (3)

Выражения (2) и (3) предполагают полную загрузку транспортных средств. На практике при расчете интервала движения учитывают и показатели рентабельности. Существенное влияние на нее оказывает уровень заполняемости транспорта L (Loading), при котором сохраняется рентабельность перевозок. Тогда эффективная вместимость транспортного средства может быть найдена как:

D = C L, (4)

где 0 <L≤ 1.

Тогда (2) и (3) будут выглядеть как:

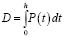. (5)

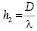. (6)

С учетом (4) h1≥h1.

Второй поход к расчету параметров ТС ориентирован на потребителей услуг и опирается на задание среднего времени ожидания, которое пассажиры проводят в очереди T (Time Waiting). Для постоянного потока пассажиров с P(t) = λ интервал движения может быть найден как:

h = 2 Tw (7)

поскольку время ожидания равно

.

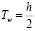Остается только определить C из (3):

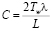. (8)

Интересы акторов транспортного процесса противоречивы. Перевозчики заинтересованы в максимальном заполнении транспорта (1.3), а пассажиры в минимальном времени ожидания – (1.8). Противоречивость интересов участников переводит процесс планирования работы ТС в разряд задач многокритериальной оптимизации. В какой-то мере коэффициент L позволяет балансировать интересы. Потоки пассажиров подчиняются многочисленным ритмам – суточным, недельным, сезонным. Они зависят и от графика проведения массовых мероприятий – спортивных соревнований, фестивалей, политических митингов. Это учитывается при составлении расписания движения транспорта – интервалы в течение суток изменяются. В управлении доминирует тенденция к жесткому их соблюдению до очередного переопределения.

Соотношения (1) – (8) используются для расчета параметров ТС, в которых на маршруте есть только один перевозчик, т.е. отсутствует конкуренция. В реальном мире за пассажиров идет конкурентная борьба между несколькими компаниями, предлагающими различные условия перевозок. Статическое планирование не может обеспечить реакцию на динамические изменения характеристик потоков пассажиров и состояния транспортных магистралей. Низкая эффективность работы программно-аппаратных комплексов управления ТС может быть связана с тем, что они не учитывают конкуренцию на рынке транспортных услуг. Для решения этой проблемы необходимо ввести новые оценки качества алгоритмов управления, в частности их способность оптимизировать работу объекта управления при воздействии на него конкурирующих субъектов. Этой цели можно достичь при создании моделей конкурирующих ТС и исследовании их функциональности в широком диапазоне параметров [1, 2, 5].

Большинство стратегий реализует только статическое управление, что не дает возможности использовать их в динамических конкурирующих системах. Необходимо найти подходы, учитывающие интересы не только источников заявок, но и их исполнителей в условиях динамического воздействия на ТС со стороны конкурирующих субъектов. При каких параметрах будет обеспечиваться оптимальное качество обслуживания пассажиров и рентабельность транспортных предприятий в условиях конкуренции? Соотношения (1)-(8) не дают возможности найти ответ на этот вопрос. Формально задача сводится к многокритериальной оптимизации и для ее решения может быть использовано имитационное моделирование. Для определенности рассмотрим конкуренцию между двумя ТК (рисунок), одна из которых (ТК1) является государственной, а вторая частной (ТК2).

Конкуренция транспортных компаний

Конкурирующие компании делят поток пассажиров P(t). При этом выполняется соотношение:

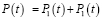. (9)

Цель конкуренции заключается в увеличении прибыли, которая в нашем случае будет зависеть от той доли пассажиров, которую удастся перевести ТК. Поэтому, будем оценивать успехи компаний по динамике соотношения 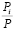. Если оно растет, стратегия управления будет выигрышной, а если падает, то проигрышной. Имитационная модель, создаваемая для проведения исследований оптимальности стратегий поведения ТК в условиях конкуренции, должна иметь возможность численной оценки вариабельности параметров управления. Для этого необходимо определить критериальные функции, отражающие конкурентные преимущества. В основе конкуренции между ТК лежит поведение пассажиров, которые формируют свои предпочтения при выборе средства передвижения. Это должно быть реализовано и в модели, например, в виде критериев, которые должны обладать свойствами информативности и вычислимости для всех стратегий управления.

Основной задачей проводимых исследований является повышение эффективности работы аппаратно-программных управляющих комплексов, поэтому ограничимся рассмотрением только тех, влияние которых легче формализовать:

– длина очереди – коэффициент a1;

– соотношение стоимостей поездки, льготы – коэффициент a2;

– время ожидания транспорта – коэффициент a3.

Если ограничить значения коэффициентов диапазоном от 0 до 1, то это позволит получить обобщенный коэффициент, определяющий предпочтения пассажира в конкурентной среде:

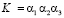. (10)

Имитационные модели, опирающиеся более чем на один подход, относятся к классу гибридных.

Библиографическая ссылка