Способы, которые базируются на трассировке лучей, по своей сути являются детерминированными, их применяли в сфере компьютерной графики, чтобы была обеспечена визуализация для реалистичных изображений [4]. В подобных подходах используют разложение электромагнитных полей по лучам и происходит поиск лучей, которые ведут к соединениям базовых и мобильных станций, когда учитываются разные особенности городских застроек.
Существуют зависимости применяемых алгоритмов от того, какие из лучей выбираются, для которых при распространении на мобильные станции мы будем наблюдать отражения на базе зеркальных или диффузных способов от стен строений. На настоящее время существуют модели для того, чтобы проводить предсказание механизмов распространения радиоволн внутри помещений. Подход может основываться на расчетах по доминирующим направлениям для распространения радиосигналов внутри помещений [2, 3]. При анализе подходов можно рассматривать дерево отношений для комнат в строениях, а для деревьев ветви применяют, чтобы определить доминирующие направления. Помимо этого, есть возможности для проведения исследований на базе нейронных сетей. Требуется применять разработанные алгоритмы в условиях, соответствующих городской застройке. В подходах по используемым вычислительным алгоритмам могут содержаться данные, которые по критериям хуже, чем когда рассматривают прямые трассировки лучей. Если говорить об используемых подходах в условиях сложных застроек, то ошибка будет больше, по сравнению с другими детерминированными подходами.
Для первого шага строят дерево, в соответствии с распространением лучей, при этом в корне будет луч, проходящий от передатчика и для каждой из точек при процессе отражений или дифракций возникает дополнительный луч, то есть, имеем рекурсию. Глубину рекурсии рассматривают как исходный параметр.
Потом на основе деревьев, связанных с распространением лучей, идет рассмотрение по всем направлениям распространения для определенного приёмника. Затем осуществляют процесс преобразования двумерных картин распространения лучей в трёхмерные, и, применяя соответствующие формулы, делают расчеты лучей по отражению и дифракции. Для разных вариантов анализируют параллельно-перпендикулярного вид застроек. Можно наблюдать создание таких моделей, в которых есть два типа лучей. Первый тип обусловлен отраженными лучами, для них проводится анализ направлений движения на базе проводящихся отражений для главных и перпендикулярных улиц. Второй тип определяется лучами, в которых есть отраженные и дифрагированные составляющие, в нем есть лучи, которые отражаются при движении по главным улицам, идет дифракция на углах улиц [5] и при отражении происходит движение по перпендикулярным улицам.
В итоге, важно отметить, что разные детерминированные способы, применяемые при оценках характеристик электромагнитных волн в условиях сложных рельефов местностей, весьма высокая точность характерна для трассировки лучей. Для погрешностей при проведении расчетов обычно получают 1-3 дБ. Но даже когда применяются подобные алгоритмы можно получить большие вычислительные возможности. Как результат, проблемы, связанные с повышением скорости вычислений с сохранением характеристик точности являются весьма актуальными.
В настоящее время, при проектировании беспроводных систем связи, возникает множество проблем связанных как с определением зоны покрытия и уровня сигнала, так и с оптимальным расположением базовых станций (БС).
Задача топологического проектирования является особенно актуальной, ввиду того, что сложный рельеф местности или сложная городская застройка вносит свои, порой значительные, коррективы на уровень сигнала, и, соответственно, на зону обслуживания беспроводных систем связи.
При проектировании систем беспроводного доступа, в настоящее время руководствуются учётом как минимум, следующих параметров [1]:
– расстояние от базовой станции до антенны пользователя (группы пользователей);
– число пользователей, их тип, а также вид услуг, которые им будут предоставляться, то есть требуется, чтобы проводилась оценка нагрузок на базовые станции.
Когда развертывается сеть, требуется, чтобы проводилось планирование того, как размещаются базовые станции. Это делаются для того, чтобы определить оптимальное, как параметрам стоимости, так и по параметрам качества доступа, размещения БС.
Формально условие задачи может быть обозначено таким образом: существует М мест-кандидатов по размещению станций, N видов станций, K клиентов. По каждому типу станций есть информация по ограничению для суммарной ширины канала по всем подключенным к станции пользователей (рассматривают производительность). Важно сделать размещение станций по соответствующим местам и сделать подключение абонентов к станциям, при этом обеспечив минимизацию полную стоимости комплекса [1].
В данном случае решается задача минимизации целевой функции стоимости, тогда рассматривают систему псевдобулевых ограничений, относительно которых анализируется решение [1]. Псевдобулевы ограничения – особая форма ограничений с конечной областью, где все переменные определены в области {0,1}. Понятно, что осуществлять решение на основе метода полного перебора не представляется целесообразным. Полученную задачу псевдобулевой оптимизации можно решить, воспользовавшись достаточно эффективным для этих целей способом – методом ветвей и отсечений.
При выборе оптимального местоположения базовой станции большое внимание уделяется излучаемой мощности, что в свою очередь влияет на зону обслуживания. Другими словами, чем выше мощность излучаемая в эфир, тем радиус зоны обслуживания больше, но при этом теряется количество абонентов, которые могут воспользоваться услугами связи [8] – [9].
В данной статье предлагается алгоритм по оптимальному распределению базовых станций на заданной территории.
Расчёт производится относительно двух соседних базовых станций:
1. Из точек О1 и О1 под углом α = β = 600 проводим прямые и находим точку пересечения (О3 – центр следующей БС) (рис. 1).
В случае если расстояние от центра БС до каждой из границ покрываемой области больше максимального радиуса (Rmax), то необходимо изменять углы α и β до тех пор, пока расстояния от центра БС до границ соседних БС не станут равными Rmax. В случае, представленном на рис. 1 выбираются отрезки KО3 и FО3.
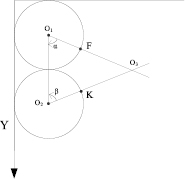
Рис. 1. Определение местоположения БС
2. Если расстояние от центра базовой станции до хотя бы одной из границ покрываемой области меньше максимального радиуса (Rmax) (рис. 2), то углы α и β изменяются до тех пор, пока перпендикуляры, опущенные из центра базовой станции на стороны покрываемой области, не станут равными (или больше) расстоянию до границы соседних БС (относительно которых производится расчет) (рис. 3).
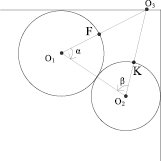
Рис. 2. Расчёт относительно границ
Из рис. 2 видно, что новое место для установки БС располагается на границе покрываемой области (О3). В связи с этим необходимо провести коррекцию местоположения точки О3, таким образом, чтобы зона обслуживания находилась в пределах ограниченной области и зоны всех соседних БС касались поперно друг друга.
Для нахождения оптимального местоположения, необходимо изменять углы α и β, пока не будет найдено оптимальное место. На рис. 3 показано найденное место для установки БС (О3), при этом отрезки (FО3), (KО3) и (GО3) будут равной длинны и равны радиусу обслуживания новой БС. Отрезок (LО3) будет больше чем (GО3), при этом установка дополнительной БС смежной с О3 невозможна, из-за того, что радиус получающейся окружности будет весьма мал.
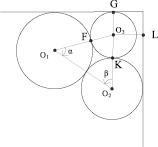
Рис. 3. Скорректированное место установки БС
3. Если БС установлена, то в матрицу смежности заносится информация о двух соседних БС (для рисунка 3 – О1О3 и О2О3), и удаляется информация о БС на основе которых была построена текущая (для рис. 3 – О1О2). Далее происходит проверка матрицы смежности на наличие соседних базовых станций, если таковые имеются, то происходит переход к шагу 1.
Установка БС прекращается, когда в матрице смежности будут отсутствовать хотя бы две БС.
Библиографическая ссылка
Яньшин Д.В. ОСОБЕННОСТИ РАЗРАБОТКИ АЛГОРИТМА ДЛЯ ПРОЕКТИРОВАНИЯ БЕСПРОВОДНЫХ СИСТЕМ СВЯЗИ // Международный студенческий научный вестник. 2017. № 4-7. ;URL: https://eduherald.ru/ru/article/view?id=17638 (дата обращения: 06.04.2025).

