Кривые с древнейших времен привлекали к себе внимание ученых и использовались ими для описания различных природных явлений – от траектории брошенного камня до орбит космических тел.
Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся без скольжения по прямой, по окружности или другой кривой, называется циклоидальной, что в переводе с греческого языка означает «кругообразная, напоминающая о круге»[1].В 1590 году Г. Галилей, изучая траекторию точки катящейся окружности, построил циклоиду и дал ей название.
Обычно выделяют три типа циклоидальных кривых:
- трохоида (частный случай – циклоида) – окружность катится по прямой;
- эпитрохоида (эпициклоида) – окружность катится по внешней стороне другой окружности;
- гипотрохоида (гипоциклоида) – по внутренней стороне.
Задача нашего исследования – установить зависимость вида кривой циклоиды на графике от параметров её уравнения.
Из параметрических уравнений мы видим, что вид графика циклоиды зависит от радиуса производящего круга, от расстояния между точкой М и центром окружности.
x = a(t – sin t), y = a(1 – cos t).
Проведём исследование графиков циклоиды с помощью системы математических и инженерных расчётов MathCAD. С помощью имеющегося набора инструментов и функций произведем ряд расчетов и построений графиков при различных исходных параметрах уравнений, описывающих циклоиды.
Рассмотрим первый случай, когда точка М лежит на производящей окружности, т. е. a = b, где a = r – радиус производящей окружности, b = d – расстояние от центра производящей окружности до точки М [1, 10].
Циклом будем называть один оборот производящей окружности вокруг своей оси в горизонтальной плоскости.
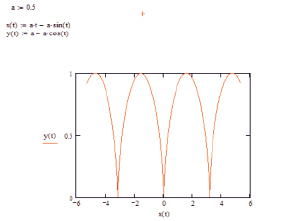
Рис. 1. Исследование первой модели в системе MathCAD
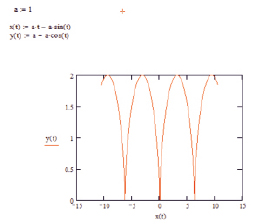
Рис. 2. Исследование первой модели с изменёнными параметрами
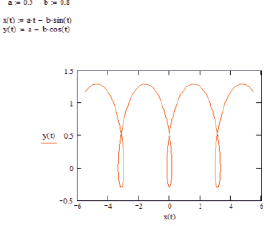
Рис. 3. Исследование удлинённой циклоиды
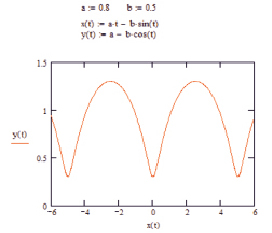
Рис. 4. Исследование параметров уравнения укороченной циклоиды
Из рис. 1 мы видим, что амплитуда циклоиды равна 1, а цикл равен 3.
На рис. 2 мы видим, что при исследовании уравнения с другими параметрами амплитуда кривой равна 2, а период примерно равен 7.
Сравнивая полученные результаты, мы можем сказать, что в случае, когда точка М расположена на производящей окружности, увеличение радиуса данной окружности ведет к увеличению амплитуды циклоиды и её периода.
Рассмотрим второй случай, когда точка М расположена вне производящей окружности, т.е. d > r (рис. 3). Такая циклоида называется удлиненной.
Здесь, также как и в первом случае, с увеличением радиуса производящей окружности увеличивается период циклоиды, а с увеличением расстояния от точки М до центра окружности, растет амплитуда.
Третий случай, когда точка М лежит внутри производящей окружности, т.е. r > d представлен на рис. 4. Такая циклоида называется укороченной.
В этом случае, как и в первых двух период циклоиды зависит от радиуса производящей окружности, а амплитуда всегда меньше её диаметра.
Таким образом, с помощью программного комплекса системы математических и инженерных расчётов MathCAD при использовании необходимых инструментов для построения графиков функций и вычислительных механизмов, был проведён ряд расчетов и построений при различных исходных параметрах уравнения циклоиды [4, 5, 9]. На базе проведённых исследований установлена зависимость формы графика от таких исходных данных как диаметр задающей окружности, расположение и удаленность от ее центра чертящего острия. Полученные результаты будут использованы при разработке информационно-образовательной среды [2, 3, 6, 7, 8, 11] кафедры общенаучых дисциплин Армавирского механико-технологического института.
Стоит заметить, что все проведённые нами исследования были применены лишь к одному виду циклоидальных кривых – простой циклоиде.
Нами запланирована серия экспериментов с варьированием параметров и изменением вида графиков для типа Эпициклоиды и Гипоциклоиды (речь идёт о кривых раскатывания, принадлежащих окружности радиуса R, которые перемещается в пределах другой окружности произвольного радиуса).
В данном случае, к числу варьируемых параметров будет добавлен также радиус окружности, по которой катится производящая циклоиду окружность.
Циклоидальные кривые применяются при многих технических расчетах и свойства их используются, например, при построении профилей зубьев шестерен, в циклоидальных маятниках, в оптике и, таким образом, изучение этих кривых важно с прикладной точки зрения.
Библиографическая ссылка
Довгалёв А.Ю., Горовенко Л.А. МЕТОДЫ ИССЛЕДОВАНИЯ ПАРАМЕТРОВ УРАВНЕНИЯ ЦИКЛОИДЫ // Международный студенческий научный вестник. 2017. № 4-7. ;URL: https://eduherald.ru/ru/article/view?id=17611 (дата обращения: 06.04.2025).

