MEMS датчики ориентации получили широкое распространение благодаря развитию различного рода техники и бесплатформенных инерциальных навигационных систем. При этом вопросы анализа погрешностей, а также калибровки MEMS акселерометров и магнитометров приобретают первостепенное значение [2 – 4, 6, 9].
Целью работы является повышение точности работы систем ориентации мобильных объектов. Достижение цели обеспечивается за счет решения задачи калибровки MEMS акселерометров и магнитометров путем идентификации параметров эллипсоида чувствительности датчиков и определения корректирующих коэффициентов для приведения его к канонической сфере.
Анализ погрешностей измерений
Главным источником погрешностей MEMS акселерометров можно считать конструкцию самого датчика. В связи с неточным размещением на плате происходит рассогласование показаний. Так же погрешностью является смещение системы координат сенсора относительно системы координат платы и неединичный масштаб осей [3 – 4, 9]. MEMS магнитометры имеют схожие погрешности, основными источниками которых являются:
– наличие магнитного наклонения, которое обусловлено особенностью магнитного поля Земли;
– наличие искусственных полей вокруг датчика, создаваемых, например, магнитами двигателей, проводами питания, аккумуляторными батареями и др. Такие погрешности носят название Hard Iron [5, 8, 10];
– искажения, вызванные наличием ферромагнитных материалов рядом с датчиком или Soft Iron [5, 8, 10]. Таким материалом может быть корпус двигателя, проводка, металлические болты крепления.
Soft и Hard Iron оказывают значительное влияние на показания магнитометра. Hard Iron вызывает смещение осей координат облака данных, а Soft Iron, в свою очередь, вносит изменения в масштабность осей координат, а также поворот эллипсоида данных вокруг начала координат.Учитывая схожесть погрешностей, присущих датчикам, процедура калибровки применима как для MEMS акселерометров, так и для магнитометров.
Постановка задачи калибровки
Стохастическая интерпретация процедуры идентификации параметров погрешностей, присущих датчикам, подразумевает концепцию «эллипсоида чувствительности», когда реакция датчика представляется как точка в трехмерном пространстве. В реальном случае из-за наличия погрешностей точки образуют облако данных в виде эллипсоида со сдвинутым центром, который может быть повернут относительно начала координат.
Таким образом, задачей калибровки становится определение коэффициентов в уравнении преобразования эллипсоида в сферу [7]:
.
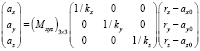Для устранения погрешностей смещения системы координат необходимо центрировать данные. В таком случае калибровка будет иметь вид [1]:
, 
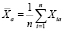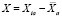
где Xia – числовые компоненты точек облака данных; Xa – среднее компоненты; X – матрица центрированных данных.
Также при калибровке магнитометра необходимо учитывать разницу между географическим и магнитным полюсами, которая зависит от местоположения, в котором проводится измерение. Для устранения этих различий к показаниям датчика необходимо прибавить или вычесть определенный угол, называемый магнитным склонением.
Вектор оценок параметров модели определяется с помощью метода наименьших квадратов (МНК). Он позволяет минимизировать сумму квадратов отклонений экспериментальных точек от эталонных:
,
,
, 
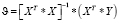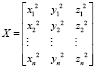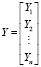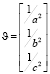
где X – матрица объясняющих переменных; Y – вектор экспериментальных результатов;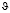 
– вектор оценок параметров.
Так решение задачи калибровки реализует идентификацию эллипсоида чувствительности по облаку точек, что, в отличие от детерминированных методов, позволяет определить не только сдвиг нуля и статистически обоснованно оценить коэффициенты усиления, но и определить ориентацию чувствительных осей.
Результаты экспериментальных измерений
В работе [2] представлены результаты имитационного моделирования на примере акселерометра ADXL345. Метод показал свою работоспособность при обработке облака неполных данных, при этом погрешность составляет порядка 1-2 %.
Экспериментальные измерения проводились с помощью датчика MPU-9265. На рис. 1 и 2 представлены данные на фоне эталонного эллипсоида чувствительности акселерометра и магнитометра соответственно. После калибровки погрешность данных составляет менее 1 %.
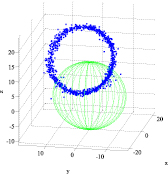
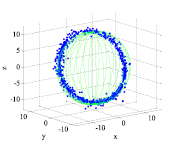
а б
Рис. 1. Облако данных на фоне эталонного эллипсоида чувствительности MEMS акселерометра: а – некалиброванного; б – калиброванного
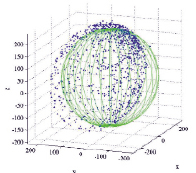
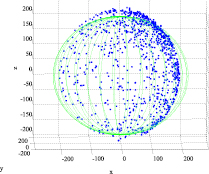
а б
Рис. 2. Облако данных на фоне эталонного эллипсоида чувствительности MEMS магнитометра: а – некалиброванного; б – калиброванного
Заключение
Предложенный метод позволяет избавиться от погрешности смещения нуля, а также скомпенсировать неединичный масштаб осей датчиков и погрешность угловой ориентации магнитометра. Основным преимуществом метода вычисления вектора оценок с помощью МНК является возможность производить вычисления без привязки к системе координат. Большее значение это имеет при калибровке магнитометра, когда можно не учитывать угол наклона и производить калибровку автономно, без гироскопа или акселерометра.
Библиографическая ссылка
Горянина К.И., Лукьянов А.Д. МЕТОД ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ ЭЛЛИПСОИДА ЧУВСТВИТЕЛЬНОСТИ MEMS ДАТЧИКОВ ОРИЕНТАЦИИ В СТОХАСТИЧЕСКОЙ ПОСТАНОВКЕ // Международный студенческий научный вестник. – 2017. – № 4-6. ;URL: https://eduherald.ru/ru/article/view?id=17581 (дата обращения: 23.11.2024).