С 2016 года в Российской Федерации вступил в силу новый криптографический стандарт ГОСТ Р 34.12-2015 «Информационная технология. Криптографическая защита информации. Блочные шифры» [1, с. 2]. В его состав вошли два алгоритма шифрования: ранее действовавший стандарт шифрования ГОСТ 28147-89 (переименован в «Магма») и новый блочный алгоритм шифрования Кузнечик.
Магма представляет собой симметричный блочный алгоритм шифрования с размером блока входных данных 64 бита, секретным ключом 256 бит и 32 раундами шифрования.
Линейный метод анализа
В связи с тем, что шифр Магма вошел в состав нового стандарта шифрования, его анализ является актуальной задачей. Исходя из того, что шифр Магма имеет фиксированные блоки замены (таблицы перестановок), его анализ с точки зрения линейного метода криптоанализа является актуальным.
Метод линейного криптоанализа впервые предложен в начале 90-х годов XX века японским ученым М. Матсуи и основывается на том, что существует возможность замены нелинейной функции ее линейным аналогом.
Ранее был проведен анализ блоков замены для алгоритма шифрования Магма. С результатами анализа можно ознакомиться в работе [2]. В ней показано, как, используя линейные свойства S-блоков замены, строить статистические аналоги для одного раунда шифрования. В результате, для первого блока замены для пары векторов
(α, β) = (1101, 0001), получим линейный статистический аналог:
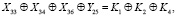(1)
для которого вероятность того, что Q = 0, равна 0,25.
Однако для проведения анализа алгоритма шифрования этого не достаточно, так как во всех аналогах в левой части присутствуют неизвестные элементы, а именно значения Y.
Аналоги, пригодные для анализа, не должны содержать в себе неизвестных битов, кроме битов секретного ключа, которые необходимо найти в результате анализа. В связи с этим необходимо разработать механизмы, которые бы позволили объединить несколько линейных аналогов в один, исключив при этом биты, которые мешают проведению анализа.
Рассмотрим один из вариантов объединения линейных аналогов. Для этого возьмем линейный аналог, полученный для первого раунда шифрования. В нем присутствует бит Y25. Обратимся к рис. 1, из которого видно, что сообщение Y1 можно получить, сложив по модулю два левую часть входного сообщения X и сообщение B, поступающее на вход функции F второго раунда шифрования. Таким образом, бит Y25 можно представить как:
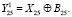(2)
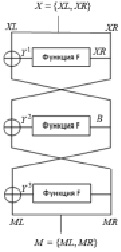
Рис. 1. Обозначения входов и выходов трех раундов шифра Магма
Теперь обратимся к третьему раунду шифрования и построим еще один линейный аналог с использованием той же пары векторов (α, β) = (1101, 0001), которая была использована для построения первого аналога. Для этого подробно рассмотрим прохождение битов сообщения через функцию F третьего раунда шифрования (рис. 2).
Рис. 2. Функция F для третьего раунда шифрования
Рассмотрим третий раунд шифрования. На вход функции F третьего раунда шифрования поступает 32-х битовая правая часть выходного сообщения M33–64. Последовательность M33–64 складывается по модулю 2 с третьим раундовым подключом K65–96 (в соответствии с принципом выработки раундовых подключей для шифра Магма третий подключ содержит 65–96 биты исходного секретного ключа K). После сложения с подключом данные разбиваются на группы по 4 бита и поступают на вход соответствующих блоков замены. На рис. 2 показано побитовое представление данных при их прохождении через функцию F третьего раунда шифрования.
Для того, чтобы определить, какие биты будут получены на выходе каждого из блоков замены, необходимо к последовательности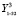 
применить операцию циклического сдвига вправо на 11 разрядов.
После того, как получено внутренне представление битов, можно перейти легко построить линейный статистический аналог для первого блока замены, определенный парой векторов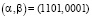 
:
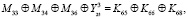(3)
для которого вероятность того, что Q = 0, равна 0,25.
В последнем линейном аналоге присутствует бит 
. Обратимся к рис. 1, из которого можно видеть, что сообщение Y3 можно получить, сложив по модулю два левую часть выходного сообщения Y и сообщение B, поступающее на вход функции F второго раунда шифрования. Таким образом, бит 
можно представить как:
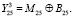(4)
Путем сложения можем объединить аналоги (1) и (3):
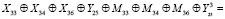
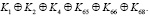(5)
Подставив в формулу (5) формулы (2) и (4), получим:
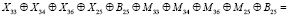
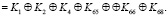(6)
В результате такого объединения двух аналогов, а также в результате представления значений на выходах функций F (значения Yi) в виде суммы по модулю два соответствующих входных (биты Xi) или выходных (биты Yi) значений и значения на входе второго раунда шифрования (значения Bi) мы получили линейный статистический аналог (7), в котором неизвестными переменными являются только биты секретного ключа.
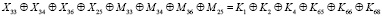(7)
В рамках исследования рассмотрен только первый этап линейного криптоанализа – анализ блоков замены и построение уравнений для одного и трех раундов шифрования. Дальнейшие исследования в области линейного анализа шифра Магма связаны с построением линейных статистических аналогов применительно к большему числу раундов алгоритма шифрования, а затем применение полученных данных к анализу полного шифра.
Слайдовый метод анализа
Метод слайдовой атаки впервые был предложен А. Бирюковым и Д. Вагнером [3, с. 245; 4, с. 589] и основан на гомогенности рассматриваемого шифра. Идея заключается в том, что можно сопоставить один процесс зашифрования с другим таким образом, что один из процессов будет «отставать» от другого на один раунд (или несколько раундов). Подробнее о применении слайдовой атаки можно прочесть в работе [5, с. 43].
Слайдовая атака
с одним раундовым подключом
В ходе исследования была рассмотрена задача поиска слайдовой пары для случая, когда в алгоритме шифрования Магма используется один и тот же раундовый подключ, что возможно, так как в Магме отсутствует функция выработки раундовых подключей. Идея заключается в том, что можно сопоставить один процесс зашифрования с другим таким образом, что один из процессов будет «отставать» от другого на один раунд. Для Магмы это теоретически возможно в 232 случаях из 2256, когда для зашифрования данных будет использоваться один и тот же раундовый подключ. Поиск слайдовой пары путем полного перебора правой части парного текста представлен на рис. 3.
В результате был разработан и реализован алгоритм, состоящий из следующих шагов:
1. Зафиксировать один текст (входную 64-х битную последовательность) и левую часть парного текста, равную правой (исходной) части фиксированного текста.
2. Определить правую часть путем полного перебора ее возможных значений (от 0х00000000 до 0хffffffff).
3. Зашифровать фиксированный текст, а также парный текст (с перебираемой на текущем этапе правой частью).
4. Проверить критерий отбора слайдовых пар: левая часть шифр-текста, полученная для фиксированного текста, должна быть равна правой части шифр-текста, полученной для парного текста, в котором перебирается правая часть. Перейти к шагу 2.
5. После полного перебора правой части парного текста сформировать результат о поиске слайдовых пар.
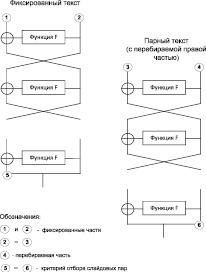
Рис. 3. Схема поиска слайдовой пары
для одного подключа
Для проведения эксперимента в локальную сеть были объединены девять ЭВМ (каждая из которых использует для вычислений два ядра), после чего был протестирован разработанный алгоритм. Результаты измерений времени поиска слайдовых пар для каждого из процессов представлены в таблице.
Результаты измерений времени поиска слайдовых пар для разных процессов
|
Имя машины – номер процесса |
Время поиска, с |
|
01–0 |
2587,870496 |
|
01–9 |
2662,572554 |
|
03–1 |
2652,869916 |
|
03–10 |
2584,051360 |
|
04–2 |
2657,906713 |
|
04–11 |
2647,533539 |
|
05–3 |
2604,300599 |
|
05–12 |
2643,880999 |
|
06–4 |
2592,802551 |
|
06–13 |
2758,090014 |
|
11–5 |
2562,219539 |
|
11–14 |
2485,150132 |
|
12–6 |
2023,647694 |
|
12–15 |
1933,766277 |
|
13–7 |
4397,100301 |
|
13–16 |
3916,700942 |
|
14–8 |
2593,235726 |
|
14–17 |
2653,619990 |
Слайдовая атака
с двумя раундовыми подключами
Также в ходе исследования была рассмотрена задача поиска слайдовой пары для случая, когда в алгоритме шифрования Магма циклически повторяются два раундовых подключа, при этом отсутствует смена порядка использования подключей в последних раундах шифрования. Таких комбинаций для различных значений двух ключей может быть 264 от общего объема ключевого пространства 2256.
Сопоставим два процесса шифрования друг с другом с отставанием на два раунда так, как показано на рис. 4.
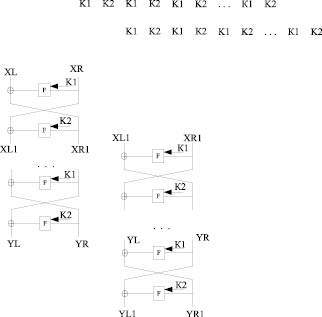
Рис. 4. Процесс шифрования с отставанием на два раунда
Предполагается, что второй открытый текст Х1 (XL1; XR1) является выходом второго раунда шифрования первого текста. Рассмотрим, как связаны между собой первый открытый текст X (XL, XR) и второй открытый текст X1 (XL1, XR1):
XR1⊕XL = F(XR, K1); (8)
XL1⊕XR = F(XR1, K2). (9)
Аналогичным образом определим, как связаны между собой шифр-тексты Y (YL, YR) и Y1 (YL1, YR1) для первого и второго открытых текстов соответственно:
YL1⊕YR = F(YR1, K2); (10)
YL⊕YR1 = F(YR, K1). (11)
В ходе исследований был разработан и реализован параллельный алгоритм поиска слайдовой пары и ключа шифрования, состоящий из следующих шагов:
1. Зафиксировать один текст (входную 64-х битную последовательность) X (XL; XR) и получить соответствующий ему шифр-текст Y (YL; YR).
2. Предположить второй текст Х1 (XL1; XR1): зафиксировать левую часть текста XL1 и определить правую часть XR1 путем полного перебора ее возможных значений (от 0х00000000 до 0хffffffff). Если такой перебор полностью осуществлен, присвоить левой части текста XL1 новое значение.
3. Получить соответствующий шифр-текст Y1 (YL1; YR1) для второго текста X1 с перебираемой на текущем этапе правой частью.
4. Из формулы (8) вычислить значение первого подключа К1.
5. Подставить найденное значение первого подключа К1 в формулу (11). Если равенство не выполняется, то вернуться к шагу 2 и переопределить правую часть XR1 путем полного перебора ее возможных значений (от 0х00000000 до 0хffffffff).
6. Из формулы (9) вычислить значение второго подключа К2.
7. Подставить найденное значение второго подключа К2 в формулу (10). Если равенство не выполняется, то вернуться к шагу 2 и переопределить правую часть XR1 путем полного перебора ее возможных значений (от 0х00000000 до 0хffffffff).
8. Если оба равенства в формулах (11) и (10) выполняются, то найдена слайдовая пара и определен используемый секретный ключ.
Направление дальнейших исследований в области слайдовой атаки на шифр Магма связано с тестированием разработанного параллельного алгоритма для случая самоподобия подключей в двух раундах шифрования, а также разработкой алгоритма поиска слайдовых пар для 4-х однотипных подключей, а затем его применение к анализу полного шифра.
Исследования, представленные в данной работе, выполнены при поддержке гранта РФФИ №17-07-00654 А.
Библиографическая ссылка
Алексеев Д.М. АЛГОРИТМ ШИФРОВАНИЯ МАГМА: ОЦЕНКА КРИПТОСТОЙКОСТИ ШИФРА С ИСПОЛЬЗОВАНИЕМ ЛИНЕЙНОГО И СЛАЙДОВОГО МЕТОДОВ АНАЛИЗА // Международный студенческий научный вестник. – 2017. – № 4-4. ;URL: https://eduherald.ru/ru/article/view?id=17410 (дата обращения: 21.11.2024).