Перед учителями во все времена математики, довольно часто стоял вопрос: «Как сделать урок более эффективным? С помощью каких приемов, методов можно заинтересовать школьников? Какие новые методы, технологии обучения необходимо использовать на уроке?»
В наше время современные образовательные технологии, стали ключевым условием повышения качества образования, снижения нагрузки учеников, рационального использования времени на уроках.
К примеру, В.И.Рыжик [3] отмечает, что около 90% учеников не будут использовать математику в дальнейшем. Действительно, студенты, которые окончили школу на «4 и 5», через пару лет забывают основные математические понятия, такие, как уравнение, функция и т.д.
Психологи установили: «Актуально осознается только то содержание, которое является предметом целенаправленной активности субъекта, т.е. занимает структурное место непосредственно цели внутреннего или внешнего действия в системе той или иной деятельности» [1].
Традиционная методика решения задач в полной мере не формирует у детей умение решать задачи, которое выполняет следующие функции: формирование мотивации и интереса к этой деятельности; выработка навыков счета, измерения, преобразования различных выражений и т.д.; решение задач наиболее удобное средство для контроля и оценки учебной работы учеников; способ приобретения учащимися новых знаний.
При решении задач, ученик главной целью ставит – найти ответ, но промежуточные действия остаются не осознанными, следовательно, умения и навыки могут не вырабатываться. Чтобы их выработать, действия должны быть непосредственной целью и актуально осознаваться.
Довольно действенным видом заданий может стать самостоятельное составление математических задач. Это способствует наиболее качественному уяснению самих задач, их структуры и механизма решения. К примеру, в младших классах можно использовать следующие задания:
1) Составление вопроса к имеющимся условиям: Как вы думаете, какие можно задать вопросы, имея данные условия?
2) Подбор условия для имеющегося вопроса: Как вы считаете, что нужно знать, чтобы дать ответ на поставленный вопрос?
3) Составление задачи по картинке, по краткой записи в виде схем, таблиц, графиков
4) Составление подобных и обратных задач.
Одна из важнейших задач в обучении математике – развитие воображения и мышления. В самом начале обучения в школе у детей развиты только наглядно-действенное и наглядно-образное мышление. И лишь только в период школьного обучения начинает развиваться рассуждение, словесно-логическое мышление, осуществляемое с помощью анализа и синтеза.
Так же нужно отметить, что «анализ» и «синтез» еще очень часто применяются для обозначения характера познания объекта. Дети сначала воспринимают объекты познания как целое (синтетически), не замечая отдельных частей – свойств и только в период подросткового возраста переходят к аналитическому взгляду на объекты познания, расчленяя объекты на части, выделяя отдельные свойства.
Также в методике обучения математике говорят об аналитическом и синтетическом методах решения задач, имея в виду ход рассуждений в процессе решения: от требования к условиям или же наоборот, от условий к требованию задачи.
Аналитический метод представляет собой логическую цепь заключений, связанных между собой. Этот метод характеризуется тем, что с вопроса задачи начинаются рассуждения. В основе этого метода решения задачи лежит умении выстраивать дедуктивные рассуждения. В таких рассуждениях нельзя получить ложное заключение из истинных посылок. Поэтому, в математических доказательствах используются дедуктивные рассуждения.
Приведем примеры задач повышенной трудности, решаемые аналитическим способом.
Пример 1. В кружках этого треугольника (рис. 1) расставьте все девять значений цифр так, чтобы суммы их на каждой стороне составляла 20.
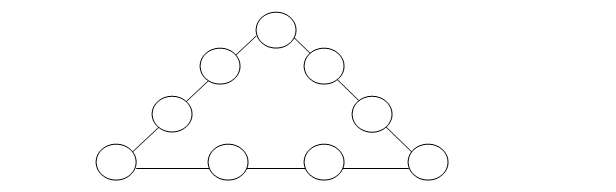
Рис. 1. Числовой треугольник
Пример 2. Какие два числа, если разделить большее из них на меньшее, дают столько же, сколько получится при их перемножении.
Пример 3. Число 30 легко выразить тремя пятерками: 5х5+5. Трудно это сделать тремя другими одинаковыми цифрами. Попробуй. Может быть, тебе удастся отыскать несколько решений.
Дедуктивные рассуждения используются при решении задач на подбор вариантов отношений. Анализ задачи в том, что мы предполагаем её решенной и ищем различные следствия решения, далее, в зависимости от вида предположений, ищем путь отыскания решения данной задачи.
Следующий метод на котором мы остановимся – синтетический. Суть синтетического метода решения задачи состоит в установлении связей между условием задачи и получении новых данных. Далее устанавливается связь между полученными данными и так, пока не будет получено требуемое. В основе данного метода решения задачи лежит умение строить индуктивные рассуждения. Выводы, полученные индуктивным путем, связаны с наблюдением, анализом. Сравнением и выявлением общих закономерностей с их последующим обобщением.
В начальной школе возможно использование двух видов индукции: полной (когда частные посылки исчерпывают все возможные случаи) и неполной. Неполная индукция является мощным эвристическим средством. Индуктивные рассуждения, как правило, используются в решении задач на комбинаторные действия.
Большинство задач решается не аналитическим или синтетическим способом в чистом виде, а сочетанием этих способов.
Аналитико-синтетический способ используется в частности при решении задач на установление соответствий между элементами различных множеств. Под множеством здесь понимается коллекция, собрание объектов, объединенных по некоторому признаку. Предметы, входящие во множество, называются его элементами.
Решению таких задач помогает использование таблиц и графиков. Если в рассматриваемой задаче каждому элементу первого множества должен соответствовать единственный элемент второго множества, а двум различным элементам первого множества соответствуют два различных элемента второго множества, то такое соответствие называется взаимнооднозначным.
Приведем примеры задач, решаемые аналитико-синтетическим методом.
Пример 4. Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас блондин, другой – брюнет, третий рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?
Решение. Для решения задачи мы воспользуемся таблицей (таблица 1), отмечая по горизонтали фамилии, а по вертикали – цвет волос. Заполняя таблицу, мы в каждой строке (столбце) должны получить только одну клетку со знаком «+».
Таблица 1
|
Фамилия |
Цвета волос |
||
|
рыжие |
черные |
русые |
|
|
Белокуров |
+ |
- |
- |
|
Чернов |
- |
- |
+ |
|
Рыжов |
- |
+ |
- |
Отсюда следует, что у Белокурова волосы рыжие, у Чернова – русые, а у Рыжова – черные.
Решение задач такого типа можно осуществлять и с помощью графов (рис. 2): элементы множества изображаются точками плоскости. Если между элементами множества есть соответствие, то будем соединять их сплошной линией.
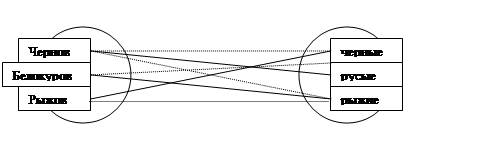
Рис. 2. Решение задач с помощью графов
Формы и методы работы с задачами повышенной трудности могут быть различны, главное, чтобы они способствовали развитию детей. Для этого они должны быть рассчитаны на «зону ближайшего развития» детей и представлять собой преодолимую трудность. Если работа над задачей будет проходить механически, то она не будет способствовать развитию математического мышления, творческой активности, навыков самостоятельного поиска решения задачи.
Конечно, для того, чтобы развить логическое мышление необходимо рассматривать различные виды задач. «Для развития логического мышления в обучении математике можно выделить такие задачи как задачи на закономерности, отличия, логические задачи, нестандартные задачи, ребусы, различные занимательные задачи, задачи на смекалку, задачи проблемного характера» [2, с. 3].
Считаем необходимым отметить, что, что в наше время, самым важным является желание детей учиться, то есть постоянная жажда знаний, а это требует правильной организации учебного процесса, он должен быть построен так, чтобы дети были увлечены, заинтересованы.
Конечно, очень и очень многое в повышении результативности и качества уроков зависит от мастерства учителя, от того, как он сумеет раскрыть тему урока, преподнести новое так, чтобы оно было понятно ученикам. Ведь урок – это педагогическое произведение, и потому он должен быть целостным, иметь внутреннюю взаимосвязь частей, единую логику развертывания деятельности учителя и учащихся.
Библиографическая ссылка
Краснолобова Е.А., Солощенко М.Ю. МЕТОДИЧЕСКИЕ АСПЕКТЫ ПРЕПОДАВАНИЯ МАТЕМАТИКИ В СОВРЕМЕННОЙ ШКОЛЕ // Международный студенческий научный вестник. 2017. № 3. ;URL: https://eduherald.ru/ru/article/view?id=17269 (дата обращения: 06.04.2025).

