Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Власова Ю.Е. 1

---

1 РЭУ им. Г. В. Плеханова

В рыночных условиях важное экономическое значение приобретает поиск оптимального варианта решения задачи, связанной с формированием производственной программы предприятия. Определение производственной программы с помощью современных моделей и математических методов оптимальных планов является одним из наиболее важных направлений поиска и дальнейшего использования внутрипроизводственных резервов и с целью повышения экономической эффективности работы предприятия. Результатом формирования плана (годового, квартального, полугодового) предприятия является установление подлежащей изготовлению номенклатуры изделий и объемов их выпуска, а также обеспечение достижения одной или нескольких целей (максимизации прибыли или объема реализованной продукции, минимизация совокупной себестоимости запланированного объема выпуска по изделиям и др.). Состав критериев оптимальности, рекомендуемых к включению в модель задачи формирования производственной программы предприятия, определяется перспективными и текущими планами развития предприятия. Наиболее важные из них включаются в экономико-математическую модель задачи. В статье рассматривается вопрос формирования производственной программы предприятия на основе максимизации прибыли в стохастические постановки задачи, основные показатели и ограничения, применяемые при использовании данного метода, а также способы реализации поставленной задачи – метод гиперболического программирования и Чарнса и Купера.

Статья в формате PDF

208 KB

гиперболического программирование

метод чарнса и купера

стохастическая постановка задачи

производственная программа предприятия

1. Закревская Е. А., Подходы и методы оценки стоимости компании в условиях рыночной экономики// Ученые записки российской академии предпринимательства 2009 № XVII. С. 168-177.

2. Лапшина Е.А., Савинова В.М., Анализ продуктов IBM для решения задач информационной бизнес-аналитики// Научные труды Вольного экономического общества России. 2012. Т. 164. С. 333-338.

При формировании производственной программы необходимо ориентироваться на потенциальные и фактические возможности предприятия по производству продукции, т.е. на производственную мощность и ограничения по годовому фонду имеющихся ресурсов.

Существует детерминированная и стохастическая постановки задачи планирования производственной программы предприятия. Стохастический подход к решению таких задач позволяет учитывать неопределённость в оптимизационных моделях.

Реальные прикладные задачи содержат либо некоторые неизвестные параметры, либо статистику изменения того или иного процесса. Этим они и отличаются от детерминированных задач оптимизации, которые формулируются с использованием заданных параметров.

Модели стохастического программирования используют знание распределений вероятностей для данных или их оценок. Цель здесь состоит в том, чтобы найти некоторое решение, которое является допустимым для всех (или почти всех) возможных значений данных и максимизируют математическое ожидание некоторой функции решений и случайных переменных. В общем, такие модели формулируются, решаются аналитически или численно, их результаты анализируются, чтобы обеспечить полезную информацию для лиц, принимающих решения.

Рассмотрим исходные данные

Таблица 1 Исходные данные по производимым продуктам

Емкость рынка по изделию 1 составляет 16 единиц

Таблица 2 Ограничения на использование ресурсов

В рамках статьи рассмотрим постановку оптимизационной задачи годовой производственной программы многономенклатурного предприятия на основе максимизации прибыли.

Общий вид оптимизационной задачи в детерминированной постановке с дробно-линейной целевой функцией и линейными ограничениями имеет следующий вид:

Ограничения:

,

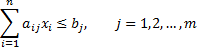
Эквипотенциали гиперболической функции в пространстве прямые, образующиеся вокруг некоторой точки. Для целевой функции

Такой точкой будет начало координат. Выражая из последнего уравнения , получим , где . Уравнение геометрически представляется прямой, проходящей через начало координат. При изменении значения F будет изменяться и , и прямая повернется вокруг начала координат. Чтобы установить поведение углового коэффициента при монотонном возрастании, необходимо взять производную от по F:

Знаменатель производной всегда положителен, а числитель не зависит от . Поэтому, знак производной постоянен, и угловой коэффициент будет либо только возрастать, либо только убывать, а прямая будет производить вращение только в одну сторону. Оптимум достигается в одной из вершин многогранника допустимых решений.

Эффективность использования тех или иных ресурсов для производства продукции является величиной случайной. Поэтому, необходимо максимизировать вероятность того, что прибыль от производства на типе j цеха будет равна или больше заданной величине ?.

Тогда задачу можно записать в виде:

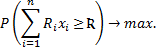
При ограничениях на производственные возможности:

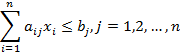
, где

Задачу в вероятностной постановке можно свести к детерминированному эквиваленту. Допустим, прибыль от эксплуатации определяется по формуле: случайная величина.

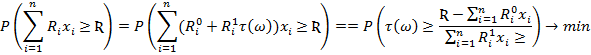
и

Получим исходя из статистики распределения прибыли. За примем минимальное значение прибыли по каждому изделию, а – среднее отклонение значений прибыли от средней величины по каждому изделию. Тогда получим:

Таблица 3 Численные значения прибыли

Численное выражение поставленной задачи имеет вид:

, ,

Для получения оптимального плана производства в поставленной выше задаче необходимо изучить алгоритмы выбранных методов поиска решения.

Первым из них является метод гиперболического программирования. Метод основан на использовании симплексной техники пересчета и специальном выборе разрешающего столбца. Ограничения поставленной задачи записываются в решающую матрицу обычным образом и дополняются базисом. Также симплекс таблица предусматривает еще три дополнительных строки: вторая и третья – это коэффициенты, стоящие в числители и знаменатели соответственно. В первой строке фиксируются признаки оптимальности. Если в исходной задаче знаменатель отличен от нуля, можно переходить к решению. Если же знаменатель обращается в ноль, необходимо сделать шаг модифицированных жордановский исключений для того, чтобы получить опорный план решения задачи. Признаки оптимальности рассчитываются по формуле =. Разрешающий столбец определяется по правилу. Выбор разрешающего элемента в столбце r проводится обычным образом – по минимальному симплекс отношению. Симплекс-таблица (за исключением первой строки) пересчитывается по рекуррентным формулам. Признаки оптимальности пересчитываются по формулам выше после пересчета остальных элементов. Критерием окончания процесса является , [1, 274-275].

Таблица 4 Исходная симплекс-таблица решения задачи оптимизации методом гиперболического программирования

В точке целевая функция не существует. Поэтому необходимо сделать шаг жордановых исключений и перейти в такую вершину выпуклого многогранника, образованного ограничениями выше, где функция существует. Применив правило получаем, что разрешающий столбец – второй. Определяя по минимальному симплекс отношению разрешающий элемент, производится пересчет таблицы по рекуррентным формулам, и получаем следующую симплекс-таблицу.

Таблица 5 Промежуточная симплекс-таблица методы гиперболического программирования

В найденной точке функция существует, и можно определить признаки оптимальности (верхняя строка полученной симплекс-таблицы). Разрешающий столбец с отрицательным числом -2452,6. Найдя в этом столбце разрешающий элемент (11) и пересчитав симплекс-таблицу, получаем следующую таблицу.

Таблица 11 Промежуточная симплекс-таблица методы гиперболического программирования

Признаки оптимальности последней симплекс-таблицы положительны, следовательно, получено оптимальное решение поставленной задачи: . Значение целевой функции получим, подставив получившиеся значения и или сменив знак у величины, стоявшей в правом верхнем углу симплекс-таблицы: f ( = 47,638.

Если учесть возможность выпуска продукции только в целых количествах, получим следующий результат: , .

Второй метод, который применяется для решения задач с дробно-линейной функций, метод Чарнса и Купера.

Задача, представленная в стандартном виде как:

В исходном виде задача представлена следующим образом:

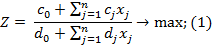
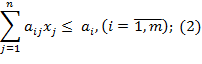
Кроме того, предполагается, что в области неотрицательных решений системы уравнений (2) имеет место .

Примем обозначение:

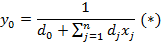
И получим новые переменные:

Из выражения (*) имеем: .

Подставим в это выражение .

Получим .

Теперь исходная задача приобретает следующий вид:

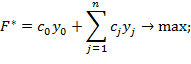
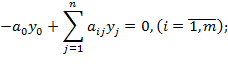
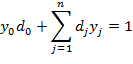
Для реализации метода Чарнса и Купера введем новую переменную:

Заменим: или

Тогда . Подставив в равенство получим: .

Теперь исходная задача приобретает следующий вид:

Решая систему выше, используя Microsoft Excel 2010 (надстройку: поиск решения), получаем следующее решение эквивалетной задачи: , f ( =47,638.

Если учитывать, что продукция выпускается в целых величинах, то получаем: , .

После того как проведены численные расчеты методом гиперболического программирования и методом Чарнса и Купера можно сделать вывод о том, что оба они привели к одному и тому же результату, а именно: , f ( =47,638. В целых значениях: , .

Оба метода схожи в реализации, оба имеют несколько итераций, результатом проведения которых является оптимальное решение поставленной задачи.

Метод гиперболического программирования имеет ряд преимуществ, например, на каждом шаге заметно, как изменяется значение целевой функции и т.д. Его несложно реализовать для задачи, когда компания реализует небольшое количество продуктов и необходимо оптимизировать их производство. С увеличением размерности, будет усложняться реализация каждой итерации, увеличиваться время на нее. Так же ошибившись на любом шаге с выбором разрешающего столбца или элемента, можно увеличить число итераций в рамках реализации задачи.

Однако, по- моему мнению, метод Чарнса и Купера проще реализовать, он может быть применен к задаче любой размерности и решение данным способом можно получить, используя простейшие компьютерные продукты, например Microsoft Excel. В результате мы получаем оптимальное решение поставленной задачи, применив лишь набольшие усилия на первом шаге по приведению задачи к линейному виду.

Библиографическая ссылка