Экономика немыслима без математики. Рыночные термины тесно переплетаются с математическими понятиями. Одним из понятий, связывающих экономику и математику является понятие полезности. Большой вклад в теорию полезности внесли Дж. Нейман и О. Моргенштерн. Они предложили процедуру построения индивидуальной функции полезности: ЛПР отвечает на ряд вопросов, обнаруживая при этом свои индивидуальные предпочтения, учитывающие его отношение к риску. Значения полезностей могут быть найдены в два этапа. На первом этапе присваиваются произвольные значения выигрышам для худшего и лучшего исходов, причем первой величине ставится в соответствие меньшее число. На втором этапе игроку предлагается на выбор: получить некоторую гарантированную денежную сумму v, находящуюся между лучшим и худшим значениями S и s, либо принять участие в игре, т.е. получить с вероятностью p наибольшую денежную сумму S и с вероятностью (1–p) – наименьшую сумму s. При этом вероятность нужно изменять до тех пор, пока ЛПР станет безразличным в отношении к выбору между получением гарантированной суммы и игрой. В общем случае график функции полезности может быть трех типов: 1 – для ЛПР, не склонного к риску,- строго вогнутая функция (рис. 1а); 2 – для ЛПР, безразличного к риску, – прямая линия (рис. 1б); 3–для ЛПР, склонного к риску, – строго выпуклая функция (рис. 1в);
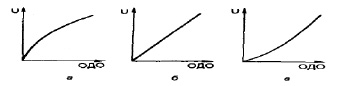
Рис. 1
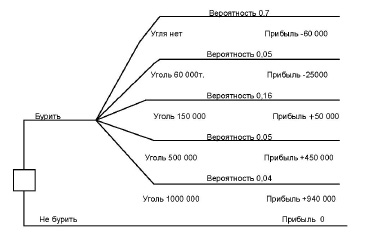
Рис. 2
При решении задач принятия решений для описания интересов ЛПР используют функцию полезности. Приведу в пример задачу, в которой использую функцию полезности (рис. 2). Углеперерабатывающее предприятие решает вопрос о бурении скважины. Известно, что если предприятие будет бурить, то вероятность того, что угля найдено не будет равна 0,7; с вероятностью 0,05 запасы месторождения угля составят 60 000 т; с вероятностью 0,16 – 150 000 т; с вероятностью 0,05 – 550 000 т; с вероятностью 0,04 – 1 000 000 т. Если угля не будет найдено, то предприятие потеряет 60 000 дол.; если мощность месторождения составит 60 000 т, то потери снизятся до 25 000 дол.; мощность месторождения в 150 000 т принесет прибыль 50 000 дол.; 550 000 т – 450 000 дол.; 1 000 000 т – 940 000 дол. Дерево решений данной задачи представлено на рис. 4. Нетрудно рассчитать ожидаемое значение выигрыша: ОДО = 0,7(–60 000) + 0,05 (–25 000) + +0,1650 000 + + 0,05450 000 + +0,04940 000 = 24 850.
Теперь обратимся к процедуре построения индивидуальной функции полезности, которую предложили Дж. Нейман и О.Моргенштерн. Для этого рассчитаем полезность результата любого из возможных исходов задачи по формуле
U () = p0 U (S ) + (1 – p0)U(s).
Присвоим произвольные значения полезностей выигрышам для худшего и лучшего исходов, причем первой величине ставится в соответствие меньшее число. Например, для нашей задачи U(–50 000 дол.)=0, а U(940 000 дол.)=40. Учитывая, что U –индивидуальное число, характеризующее ЛПР, нули, отвечающие расчету одо,можно отбросить. Рассчитаем полезность результатов любого из возможных исходов для задачи. Пусть для ЛПР безразлично: потерять 20 000дол.или начать раскопки угля(выигрыш 940 000 дол. с вероятностью 0,1 или проигрыш 50 000 дол. с вероятностью 0,9.) согласно формуле имеем: U(–20)=0.1 U(940)+0.9 U(–50)=4 Получаем U(-50)=0, U(940)=40, откуда следует, что U(–20)=4. Таким образом, может быть построена функция полезности (рис. 3).
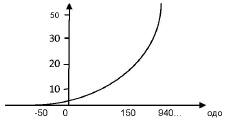
Рис. 3
Библиографическая ссылка
Ханмурзина З.Р. ФУНКЦИЯ ПОЛЕЗНОСТИ НЕЙМАНА-МОРГЕНШТЕРНА // Международный студенческий научный вестник. 2016. № 4-4. ;URL: https://eduherald.ru/ru/article/view?id=16413 (дата обращения: 05.04.2025).

