Математическая модель – это приближенное описание объекта моделирования, выраженное с помощью математической символики.
Математические модели появились вместе с математикой много веков назад. Огромный толчок развитию математического моделирования придало появление ЭВМ. Применение вычислительных машин позволило проанализировать и применить на практике многие математические модели, которые раньше не поддавались аналитическому исследованию. Реализованная на компьютере математическая модель называется компьютерной математической моделью, а проведение целенаправленных расчетов с помощью компьютерной модели называется вычислительным экспериментом.
Оптимизационные модели используются для описания процессов, на которые можно воздействовать, пытаясь добиться достижения заданной цели. В этом случае в модель входит один или несколько параметров, доступных влиянию. Например, меняя тепловой режим в зернохранилище, можно задаться целью подобрать такой режим, чтобы достичь максимальной сохранности зерна, т.е. оптимизировать процесс хранения.
Задача о загрузке (задача о рюкзаке) и различные её модификации широко применяются на практике в прикладной математике, криптографии, экономике, логистике, для нахождения решения оптимальной загрузки различных транспортных средств: самолетов, кораблей, железнодорожных вагонов и т.д.
Задача состоит в определении загрузки вагонов в такой последовательности, которая приносит наибольшую суммарную прибыль.
Рассматриваемая нами задача является NP - полной, то есть для нее не существует полиномиального алгоритма, решающего её за разумное время, в этом и есть проблема. Либо мы выбираем быстрый алгоритм, но он, как известно, не всегда решает задачу наилучшим образом, либо выбираем точный, который опять же не является работоспособным для больших значений.
К точным методам относятся: полный перебор, метод ветвей и границ. К приближенным: жадные алгоритмы. Полный перебор - перебор всех вариантов (всех состояний) - малоэффективный, но точный метод. Метод ветвей и границ - по сути, сокращение полного перебора с отсечением заведомо “плохих” решений. Жадный алгоритм - основан на нахождении относительно хорошего и “дешевого” решения.
Сравнительный анализ методов решения.
Минусы полного перебора:
· Входные данные не велики, для N=7 программа укладывается в 1с. Уже для N=10 требуется примерно 40с;
· Временная сложность O(N!).
Плюсы полного перебора:
· Полный перебор дает точное решение;
· Простота реализации.
Минусы метода ветвей и границ:
· В худшем случае работает как полный перебор.
Плюсы метода ветвей и границ:
· Значительное сокращение времени работы;
· Простота реализации.
Минусы жадного алгоритма:
· Всегда можно предоставить такой набор, при котором решение будет не точным.
Плюсы жадного алгоритма:
· Высокое время работы, ограниченное только скоростью сортировки, в среднем O(NlogN);
· Может работать с большими значениями N;
· Не использует дополнительных ресурсов компьютера;
· Простота реализации.
Нам нужен точный и быстрый результат, поэтому для решения нашей задачи мы выбираем метод ветвей и границ.
Метод ветвей и границ основан на идее разумного перечисления всех допустимых точек задачи оптимизации. Оговорка разумного имеет важное значение, поскольку, что должно быть уже ясно, безнадежно пытаться просто просмотреть все допустимые решения. Слово «ветвей» в названии «метод ветвей и границ» относится к процессу разбиения; слово «границ» относится к нижним оценкам, которые используются при построении доказательства оптимальности без полного перебора.
По существу, данный метод - это вариация полного перебора, с исключениями заведомо не оптимальных решений. Для полного перебора можно построить дерево решений. Если у нас есть какое-то оптимальное решение P , мы пытаемся улучшить его, но если на рассматриваемой в текущий момент ветви решение заведомо хуже, чем P то следует остановить поиск и выбрать другую ветвь для рассмотрения. Тогда используя метод ветвей и границ можно сократить дерево перебора. Но не всегда получается отсеять достаточно много вариантов чтобы скорость работы была заметно увеличена, всегда можно подобрать такие входные данные, для которых метод ветвей и границ даст оценку по времени идентичную полному перебору.
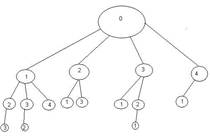
Рис. 1. Использование метода ветвей и границ
При построении дерева в алгоритме ветвей и границ для задачи целочисленного программирования (ЦЛП) требуются две вещи:
· Ветвление. Множество решений, представляемое вершиной, можно разбить на попарно непересекающиеся множества. Каждое подмножество в этом разбиении представляется сыном исходной вершины.
· Получение нижних границ. Имеется алгоритм для вычисления нижней границы стоимости любого решения в данном подмножестве.
Никакие другие свойства и задачи ЦЛП не используются. Поэтому рассматриваемый метод можно сформулировать для любой задачи оптимизации, в которой выполняются оба свойства, независимо от того, линейна или нет функция стоимости.
Формулировка модели
Пусть имеется заказ, имеющий свой объем V , и множество вагонов K , имеющих свои объемы vij , где i – номер группы по грузоподъемности, j -номер вагона в группе.
Математическая модель задачи выполнения заказа также может быть построена за счет введения булевых переменных:
![]() =
=![]()
Тогда целевая функция задачи будет иметь вид:
![]() (1)
(1)
Ограничения:
![]() (2)
(2)
![]() (3)
(3)
где V – объем заказа, – грузоподъемность одного вагона, ![]() - цена аренды вагона, Ni – количество вагонов в i - группе.
- цена аренды вагона, Ni – количество вагонов в i - группе.
Алгоритм метода:
1. Определяются все начальные данные: количество продукции в заказе b и их объем V , количество вагонов N , их объем ![]() .
.
2. Находится общий объем всех вагонов
![]() (4)
(4)
Эта величина сравнивается с объемом заказа V . Выбирается такая комбинация вагонов, для которой разница между общим объемом продукции в заказе и объемом вагонов минимальна:
![]() (5)
(5)
1. Заказ загружается следующим образом.
Берется первый вагон в количестве 1шт. и помещается в заказ. Проверяется условие
![]() (6)
(6)
Если это условие выполняется, добавляем еще один вагон, и продолжаем добавлять по одному вагону до тех пор, пока количество продукции в заказе не будет заполнено. Переходим к следующей продукции, и т.д.
Таким образом, математическая модель может быть положена в основу автоматизированной системы планирования затрат на передвижные составы.
Библиографическая ссылка
Васютина В.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМИЗАЦИИ ЗАГРУЗКИ ПЕРЕДВИЖНЫХ СОСТАВОВ // Международный студенческий научный вестник. 2016. № 2. ;URL: https://eduherald.ru/ru/article/view?id=15855 (дата обращения: 05.04.2025).

