В рамках магистерской работы предполагается разработка запросов к реляционной базе данных, содержащей информацию о системе онлайн-платежей. В настоящее время системы моментальных платежей получили широкое распространение. Во-первых, это обусловлено высокой скоростью денежных переводов по сравнению с оплатой счетов в банке. Также важным является удобство: достаточно иметь доступ в Интернет, чтобы быстро оплатить покупку или услугу, также некоторые сервисы предлагают возможность выбора валюты платежа независимо от валюты счета. Третьим достоинством является относительная безопасность электронных денег. Возможность постоянно контролировать счет, расходы и остаток является четвертым преимуществом.
Зарождение теории нечетких множеств произошло в конце 60-х годов. Нечеткий подход к моделированию получил признание во всем мире. На данный момент нечеткая логика применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений, существуют пакеты программ для построения нечетких экспертных систем.
Нечеткие запросы к базам данных – перспективное направление в современных системах обработки информации. Данный инструмент дает возможность формулировать запросы на естественном языке, например: «Вывести список обувных магазинов с невысокими ценами рядом со станцией метро Сокол», что невозможно при использовании стандартного механизма запросов. Для этой цели разработана нечеткая реляционная алгебра и специальные расширения языков SQL для нечетких запросов. Большая часть исследований в этой области принадлежит западноевропейским ученым Д. Дюбуа и Г. Праде.
Механизмы нечетких запросов к реляционным базам данных базирующиеся на теории нечетких множеств Заде, были впервые предложены в 1984 году и впоследствии получили развитие в работах Д. Дюбуа и Г. Прада.
Большая часть данных, обрабатываемых в современных информационных системах, носят четкий, числовой характер. Однако в запросах к базам данных, которые пытается формулировать человек, часто присутствует неопределенность. Например, когда на запрос в поисковой системе Интернета пользователю выдается множество ссылок на документы, упорядоченных по степени релевантности (или соответствия) запросу. Потому что текстовой информации изначально присуща нечеткость, причиной которой является семантическая неоднозначность языка, наличие синонимов и т.д.
С базами данных информационных систем, или с четкими базами данных ситуация другая. Пусть, например, из базы данных требуется извлечь следующую информацию:
• «Получить список долго работающих сотрудников с невысокой заработной платой»
• «Вывести список обувных магазинов с невысокими ценами рядом со станцией метро Сокол «
Здесь высказывания «Долго работающий», «Невысокая», «Невысокие цены», «Рядом с метро» имеют размытый, неточный характер, хотя заработная плата определена до рубля, а удаленность магазина от метро – с точностью до метра. Причиной этому является, что в реальной жизни мы оперируем и рассуждаем неопределенными, неточными категориями. Такие запросы невозможно выполнить средствами языка SQL. В этом случае необходимо использовать концепцию нечетких запросов.
Например, продемонстрировать ограниченность четких запросов можно следующим образом. Пусть требуется получить сведения о терминалах для приема платежей, расположенных в определенном регионе, по которым оборот превысил 120 000 рублей за месяц, при этом сумма отмененных платежей не превысила 1 000 рублей. Данный запрос можно записать на языке SQL следующим образом:
|
select Terminal_id from Terminals where (Terminals.Sum > 120000 AND Terminals.Otm < 1000 AND Terminals.Region_id = 56) |
Терминал с суммой принятых платежей 200 000 рублей и отменами в 1 010 рублей, или с суммой платежей 119 890 рублей и без отмененных платежей не попадут в результат запроса, хотя их характеристики почти удовлетворяют требованиям запроса.
Нечеткие запросы помогают справиться с подобными проблемами «пропадания» информации.
Для примера формализуем нечеткое понятие «Оборот терминала» (рис. 1). Это будет названием соответствующей лингвистической переменной. Зададим для нее область определения X = [0; 500 000] и три лингвистических терма – «Низкий», «Средний», «Высокий». Далее необходимо построить функции принадлежности для каждого лингвистического терма.
Выберем трапецеидальные функции принадлежности со следующими координатами:
«Низкий» = [0, 0, 110 000, 150 000],
«Средний» = [110 000, 160 000, 330 000, 390 000],
«Высокий» = [310 000, 420 000, 500 000, 500 000].
Теперь можно вычислить степень принадлежности терминала с оборотом в 140 000 рублей к каждому из нечетких множеств по трапецеидальной функции принадлежности:
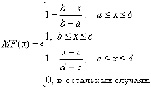
MF[Низкий](140 000)=0,25;
MF[Средний]( 140 000)=0,6;
MF[Высокий](30)=0.
Приведенных выше сведений достаточно для построения и выполнения нечетких запросов. Вернемся к примеру о терминалах. Для простоты предположим, что вся необходимая информация находятся в одной таблице со следующими полями: ID – номер терминала, SUM – сумма оборота за месяц, OTM – сумма отмен за месяц.
|
ID |
SUM |
OTM |
|
10 |
450 000 |
60 000 |
|
11 |
310 000 |
11 000 |
|
12 |
280 000 |
25 000 |
|
13 |
140 000 |
10 000 |
|
… |
||
Лингвистическая переменная «Оборот терминала» была задана ранее. Определим еще одну лингвистическую переменную для поля OTM с областью определения X = [0; 100 000] и термами “Малый”, “Средний” и “Большой” и аналогично построим для них функции принадлежности:
“Малый” = [0, 0, 0, 20 000],
“Средний” = [19 000, 25 000, 50 000, 60 000],
“Большой” = [50 000, 75 000, 100 000, 100 000].
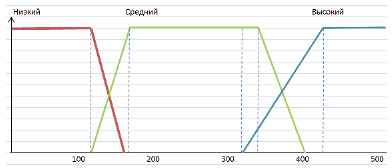
Рис. 1. Функции принадлежности лингвистических термов переменной “Оборот терминала”
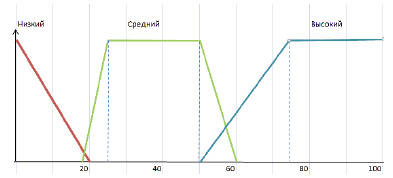
Рис. 2. Функции принадлежности лингвистических термов переменной “Отмены”
К такой таблице можно делать нечеткие запросы. Например, получить список всех терминалов с большим оборотом и маленькой суммой отмен, что на SQL-подобном синтаксисе запишется так:
|
select * from Terminals where (SUM = «Большая» AND OTM = «Маленькая») |
Рассчитав для каждой записи агрегированное значение функции принадлежности MF (при помощи операции нечеткого «И»), получим результат нечеткого запроса:
|
ID |
SUM |
OTM |
|
11 |
310 000 |
11 000 |
Записи 1,3,4 не попали в результат запроса. Записей, точно удовлетворяющих поставленному запросу (MF=1), в таблице не нашлось. На практике обычно вводят пороговое значение функции принадлежности, при превышении которого записи включаются в результат нечеткого запроса.
Аналогичный четкий запрос мог бы быть сформулирован, например, так:
|
select * from Terminals where (OTM <= 16 000 AND SUM >= 310 000) |
Его результат является пустым. Поэтому можно сказать, что нечеткие запросы позволяют расширить область поиска в соответствии с изначально заданными человеком ограничениями.
Используя нечеткие модификаторы, можно формировать и более сложные запросы.
Библиографическая ссылка
Шукшина Н.С., Воронова Л.И. РАЗРАБОТКА НЕЧЕТКИХ ЗАПРОСОВ К РЕЛЯЦИОННОЙ БАЗЕ ДАННЫХ СИСТЕМЫ ОНЛАЙН-ПЛАТЕЖЕЙ // Международный студенческий научный вестник. 2015. № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14171 (дата обращения: 09.04.2025).

