Гипотеза о равенстве средних при неизвестных дисперсиях требует вначале проверки гипотезы о равенстве дисперсий двух выборок.
Рассмотрим задачу.
Реклама утверждает, что из двух типов пластиковых карт «Русфонд» и «Супер-экспресс» обеспеченные люди предпочитают первый. С целью проверки этого утверждения были обследованы среднемесячные платежи n1 = 16 обладателей «Русфонда» и n2 = 11 обладателей «Супер-экспресса». При этом выяснилось, что платежи по картам «Русский экспресс» составляют в среднем 563 долл. с исправленным средним квадратическим отклонением 178 долл., а по картам «Супер-экспресс» – в среднем 485 долл. с исправленным средним квадратическим отклонением 196 долл.
Предварительный анализ законов распределения месячных расходов, как среди обладателей карт «Русфонда», так и среди обладателей карт «Супер-экспресса» показал, что они достаточно хорошо описываются нормальным приближением.
Проверить утверждение рекламы на уровне значимости 10 %.
В этом случае следует проверить гипотезу о средних при неизвестных дисперсиях (объёмы выборок малы). Поэтому, прежде всего, необходимо проверить гипотезу о равенстве дисперсий. Имеем:
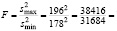1,21.
Из таблицы критических значений Фишера-Снедекора по уровню значимости α/2 = 0,05 и числам степеней свободы k1 = nmax – 1 = 10 и k2 = nmin – 1 = 15 (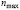
и 
соответствуют 
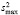и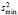 
) находим критическую точку Fкр = 2,55. Поскольку 1,21 < 2,55, принимаем гипотезу о равенстве дисперсий двух выборок.
Теперь можно воспользоваться критерием Стьюдента для проверки гипотезы о равенстве средних. Имеем
.
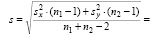
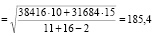Вычисление статистики критерия даёт зачение
.
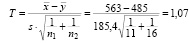По таблице критических точек распределения Стьюдента для односторонней области по уровню значимости α = 0,1 и числу степеней свободы 16 + 11 – 2 = 25 находим tкр = 1,32.
Поскольку Т < tкр, то принимается основная гипотеза о равенстве средних. Таким образом, утверждение рекламы не подтверждается имеющимися данными. Значит нельзя утверждать, что обеспеченные люди предпочитают только первый вид пластиковых карт.
Библиографическая ссылка
Сергеев Н. Е., Протопопов Н. А., Агишева Д. К., Светличная В. Б. ПРОВЕРКА ГИПОТЕЗ ДЛЯ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК ПРИ НЕИЗВЕСТНЫХ ДИСПЕРСИЯХ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14163 (дата обращения: 21.11.2024).