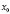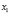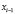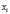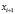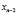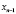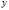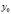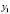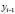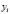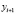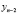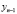Сплайны [1] имеют многочисленные применения, как в математической теории, так и в разнообразных вычислительных приложениях.
В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.
Сплайны двух аргументов называют би-сплайнами (например, бикубический сплайн), которые являются двумерными сплайнами, моделирующими поверхности. Их часто путают с B-сплайнами (базисными сплайнами), которые являются одномерными и в линейной комбинации составляют кривые – каркас для «натягивания» поверхностей.
Также из базисных сплайнов возможно составить трёхмерную конструкцию для моделирования объёмных тел.
Рассмотрим алгоритм кусочно-квадратичной интерполяции.
Пусть в результате некоторого опыта получены экспериментальные данные, которые можно представить в виде таблицы (табл. 1).
Таблица 1
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
|
|
Точки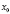 
, 
, …, 
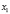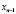называются узлами интерполяции. Все точки принадлежат отрезку [a; b], где 
, 
.
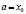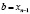Для удобства будем полагать, что узлы – равноотстоящие с шагом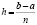 
, тогда
, 
.
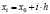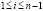Сплайном (англ. spline) называли гибкую металлическую линейку – универсальное лекало, которое использовали чертёжники для соединения точек на чертеже плавной кривой, то есть для графического исполнения интерполяции.
В вычислительной математике сплайном называется функция, которая вместе с производными непрерывна на всём заданном отрезке [a; b], но при этом на каждом частичном отрезке [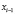
; 
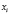] в отдельности представляется в виде некоторого алгебраического многочлена.
Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной – дефектом сплайна.
Алгоритм кусочно-квадратичной интерполяции относительно прост и включает в себя два этапа:
1) нужно найти три узла, ближайших к узлу интерполяции;
2) вычислить значение интерполяционного многочлена второй степени.
Первый этап реализуется в зависимости от регулярного или нерегулярного расположения узлов интерполяции.
Не умаляя общности, можно предположить, что узлы интерполяции расположены произвольно. Тогда, поиск ближайших точек можно осуществить в виде цикла, в котором очередной узел интерполяции последовательно сравнивается с правыми границами отрезков интерполяции.
В том случае, когда выполняется условие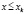 
, то для интерполяции выбираются (k-1)-й, k-й и (k+1)-й узлы.
Иначе k увеличивается на единицу.
Код программной реализации кусочно-квадратичной интерполяции сплайнами:
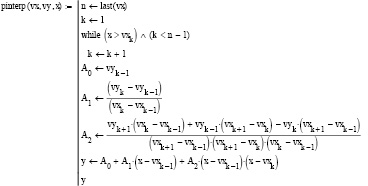
Библиографическая ссылка
Матрохин С.А., Сергиенко В.В., Агишева Д. К., Матвеева Т. А. ПОСТРОЕНИЕ КУСОЧНО-КВАДРАТИЧНОЙ СПЛАЙН-ИНТЕРПОЛЯЦИИ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14161 (дата обращения: 16.04.2024).