Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Файлы
• Литература

Ефремкин С.И. 1 Мазырина А.М. 1 Светличная В.Б. 1 Агишева Д.К. 1 Матвеева Т.А. 1

---

1 Волжский политехнический институт (филиал) Волгоградского государственного технического университета

Статья в формате PDF

341 KB

1. Матвеева Т.А., Афонасенков О.В., Агишева Д.К. Функциональные ряды, ряды и интеграл Фурье // Международный журнал экспериментального образования. – 2010. – № 12. – С. 76-77.

2. Чеботков П.Е., Светличная В.Б. Представление функции различными рядами Фурье // Успехи современного естествознания. – 2012. – № 4. – С. 55-56.

Рассмотрим разложение функции y = ex в ряд Тейлора. Из теории математического анализа известно разложение

.

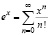Данное разложение справедливо на промежутке (– ∞; ∞) при неограниченном числе слагаемых. Но для практического использования бесконечное количество членов ряда использовать нецелесообразно.

Исследуем достаточное количество членов разложения заданной функции на промежутке [–2; 2]. Для этого используем программу MathCad. Определим заданную функцию у(х) и ряд Тейлора S(х,N), где N – достаточное количество членов разложения. Вычислим значения функции и ряда для значений 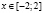с шагом 0,5.

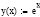
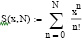
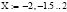
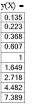
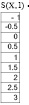
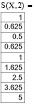
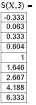
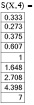
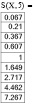
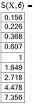
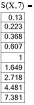
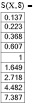
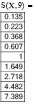
Как видно из вычислений при девяти слагаемых значения с точностью до третьего знака после запятой совпадают.

Найдём абсолютную ошибку:

Построим на одном чертеже графики у(х) и S(х,9).

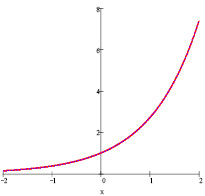
Вывод: в данном случае предпочтительнее использовать ряд Тейлора с девятью слагаемыми.

Библиографическая ссылка