Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Файлы
• Литература

Соловьева А.А. 1 Коробкина А.В. 1 Зотова С.А. 1 Агишева Д.К. 1 Светличная В.Б. 1

---

1 Волжский политехнический институт (филиал) Волгоградского государственного технического университета

Статья в формате PDF

320 KB

1. Лосева А.Ю., Агишева Д.К. Эластичность спроса // Успехи современного естествознания. – 2012. – № 4. – С. 48-49.

2. Астапенко Е.Ю., Лисник А.Ф., Немцова Е.В., Агишева Д.К., Светличная В.Б. Функции издержек в экономике // Современные наукоемкие технологии. – 2014. – № 5 (2). – С. 189-189.

3. Булашкова М.Г., Ломакина А.Н., Чаузова Е.А., Зотова С.А. Роль математики в современном мире // Успехи современного естествознания. – 2012. – № 4. – С. 45-45.

Каждый студент в процессе обучения сталкивается с вопросом: ″А понадобится ли мне математический анализ в экономических приложениях в жизни?″ Ответ да. Ведь с помощью знаний в этой области можно рассчитать прибыль компании, найти количество единиц продукции, которые необходимо продать, найти точку рыночного равновесия, а также объём выпуска, при котором прибыль производителя будет максимальной.

Прибегая к математическому анализу в экономических приложениях, производитель может найти средние издержки на производство единицы продукции, среднее приращение издержек, а также предельные издержки. Приведём пример.

У нас есть следующая функция издержек производства: Y=50x – 0,05x3 (y.e.). Найти:

1) средние издержки на производство единицы продукции, если объём выпуска продукции х0 = 10;

2) среднее приращение издержек, если объём выпуска продукции увеличится до х = 15;

3) предельные издержки.

Решение.

1) Найдём средние издержки:

y(xo)/ xo = (50x–0,05x3) / x = (50 – 0,05·x2) x = 10 =

= 50 – 0,05·102 = 45 (у.е.).

2) Найдём среднее приращение издержек:

y(10) = (50x – 0,05x3) x = 10 = 50·10 – 0,05·103= 450 ;

y(15) = (50x – 0,05x3) x = 10 = 50·15 – 0,05·153=581,25;

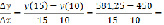
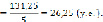
3) Найдём предельные издержки:

y`= (50x – 0,05x3)` = 50 – 0,15x2 =>

y`(10) = 35 (y.e.);

y`(15) = 16,25 (y.e.).

Сравнивая результаты, делаем вывод, что чем больше объём дополнительной продукции производства, тем меньше требуется дополнительных затрат.

Данная задача по теме математический анализ в экономических приложениях наиболее заинтересовала нас, поэтому мы представили Вашему вниманию алгоритм её решения.

Для решения подобных задач используются основные теории дифференциального исчисления для экономических объектов. Перечислим их.

Теорема №1. Оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода.

Теорема №2. Оптимальный для производителя уровень экономического производства определяется равенством средних и предельных издержек.

Теорема №3. (Закон доходности): С увеличением производства объёма дополнительной продукции, полученной на каждую новую единицу ресурса, с некоторого момента уменьшается.

Теорема №4. (Закон полезности): С увеличением производства товара дополнительная полезность от каждой его новой единицы с некоторого момента уменьшается.

Библиографическая ссылка