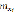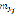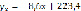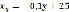Ни для кого не секрет, что между случайными величинами может существовать определённая зависимость. Один из её видов – это статистическая зависимость, которая имеет место тогда, когда при изменении одной случайной величины изменяется закон распределения другой случайной величины. Статистическая зависимость, в свою очередь, называется корреляционной, если при изменении одной из величин изменяется среднее значение другой – это зависимость в среднем, и она является функциональной.
Элементы теории корреляции занимают важное место в математической статистике, так как они имеют обширную область применения, охватывая также и экономическую сферу. В качестве примера рассмотрим следующую задачу.
Распределение 100 предприятий отрасли по объёму выпускаемой продукции X (тыс. ед.) и её себестоимости Y (руб.) представлено в таблице:
|
y x |
48 |
58 |
68 |
78 |
|
|
17 |
— |
— |
— |
1 |
1 |
|
18 |
— |
— |
29 |
1 |
30 |
|
19 |
— |
29 |
10 |
— |
39 |
|
20 |
21 |
6 |
— |
— |
27 |
|
21 |
3 |
— |
— |
— |
3 |
|
|
24 |
35 |
39 |
2 |
100 |
После проведения необходимых математических расчетов мы получили следующие данные: 
= 19,01, 
; 
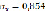= 59,9,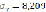 
; 
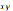= 1132,48. Условные средние значения 
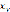и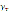 
и межгрупповые дисперсии равны: 
, 
, 
, 
, 
; 
, 
, 
, 
, 
, 
.
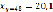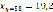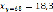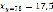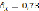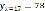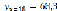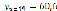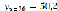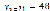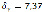Корреляционные отношения: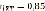 
, 
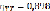, на основании чего делаем вывод, что между X и Y имеется сильная корреляционная зависимость. Коэффициент корреляции при этом равен – 0,89, что говорит нам о наличии сильной убывающей линейной зависимости. На уровне значимости α=0,05 мы наблюдаем наличие линейной корреляции. Корреляция называется линейной, если линия регрессии одной случайной величины на другую является прямой линией. Уравнения линейной регрессии выглядят следующим образом:
|
|
|
|
Полученное уравнение показывает, что при увеличении объёма выпуска X на 1 тыс. ед. себестоимость Y уменьшается в среднем на 8,6 (руб.). |
Полученное уравнение показывает, что для уменьшения себестоимости Y на 1 руб. необходимо в среднем увеличить объём выпуска X на 0,1 тыс. ед. |
Теоретический коэффициент детерминации равен 0,7921, это означает, что 79,21% вариации себестоимости продукции объясняется уравнением линейной регрессии, остальные 20,79% вариации себестоимости обусловлены влиянием неучтённых в модели факторов.
Средние квадратические ошибк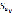и 
и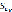 
равны 3,14 и 0,23 соответственно. Таким образом, найденные модели линейной регрессии целесообразно использовать. Средние ошибки аппроксимации составляют 2,76% и 0,675%, что свидетельствует о незначительных погрешностях моделей.
Таким образом, мы увидели, как себестоимость и объём выпускаемой продукции зависят друг от друга относительно большого числа различных предприятий. Подобную информацию целесообразно применять, например, при ведении конкурентной борьбы, а также при формировании исходных данных (себестоимость и объём выпускаемой продукции) при запуске деятельности предприятия с целью максимизации экономической прибыли.
Библиографическая ссылка
Городжий А.В., Зотова С.А., Матвеева Т.А., Светличная В.Б. ПРИМЕНЕНИЕ ТЕОРИИ КОРРЕЛЯЦИИ НА ПРАКТИКЕ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14152 (дата обращения: 21.11.2024).