Рассмотрим задачу Коши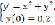 
Дифференциальное уравнение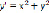 
не относится к известному типу дифференциальных уравнений I порядка. Решим уравнение двумя способами:
1) с помощью рядов;
2) графический (методом изоклин).
Считаем, что решение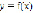 
допускает разложение в ряд Маклóрена
.
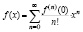Определим первые шесть слагаемых. Вычислим коэффициенты:
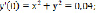
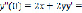0,016;
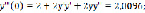
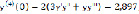
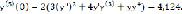
Таким образом, получили приближённое решение
.
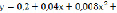
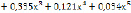Построим кривую, соответствующую найденному решению при x = {–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5}. Для этого используем систему компьютерной математики MathCAD (рис. 1).
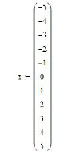
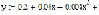
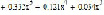
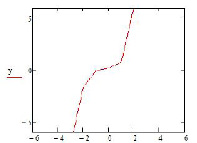
Рис. 1
Теперь решим это же уравнение графически. Построим поле направлений дифференциального уравнения, изображая изоклины: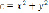 
, (c ≥ 0).
Изоклины – семейство окружностей с центром (0;0) и радиусом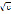 
.
1) c=0: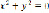 
– уравнение определяет точку (0;0) в которой tgα=0, значит α=0;
2) c=1: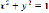
, вдоль этой изоклины отрезки поля имеют угловой коэффициент tg(α)=1, т.е. α=arctg(1) α = π/4;
3) c=4: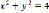 
, tgα=4, α=arctg(4)≈76°;
4) c=9: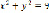 
, tgα=9, α=arctg(9)≈84°;
5) c=16: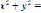 
16, tgα=16, α=arctg(16)≈86°;
6) c=25: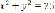 
, tgα=25, α=arctg(25)≈88°.
Используя найденные значения, построим изоклины и поле направлений (рис. 2). Далее можно провести приближённое графическое решение.
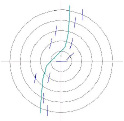
Рис. 2
Сопоставив два приближённых решения, приходим к выводу, что они графически совпадают.
Библиографическая ссылка
Брозе В.Е., Вараксин В.А., Светличная В.Б., Зотова С.А. ПРИБЛИЖЁННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14151 (дата обращения: 21.11.2024).