Фонд социального страхования – это государственная кредитно-финансовая организация, управляющая финансами социального страхования. Егокоренное отличие от рядовых страховых компаний состоит в регулярных денежных выплатах,направляемых на осуществление региональных и межотраслевых программ по охране здоровья служащих, санаторно-курортному лечению, организация учебного досуга детей.Фонд социального страхования РФ – второй по количеству задействованных финансов после Пенсионного фонда РФ. Для оптимального управления капиталом фонда необходимо решения задач математического моделирования.
Итак, рассмотрим следующую модель:
Обозначим Фонд S(t) существующий сейчас. Тогда скорость выплаты средств, находящихся на счете Фонда, на общественные программы разного рода представим как – *(S), где – c*(S) = 0 при S < S0. Соответственно, выплаты на социальные базы будут выделяться только примногократном превышении капиталом фонда определенного пограничного значения S0, что по своей природе вполне нормально, поскольку основная задача фонда: стремление максимально снизить вероятность банкротства(при S < 0) на незначительном уровне и производит лишь выплаты по страховым случаям при капитале, меньшем некоторой критической шкалы.
Найдем функцию c*(S), создающую необходимые условия стабильной работы Фонда.
Наша цель: максимально уменьшить дисперсию скорости дифференцирования капитала фонда с использованием детерминированной компоненты c(S) = c0 – c*(S) – при чем, вероятность издержек направленных на социальные программы 0 P(S > S0 ) остается неизменной.
Итак,
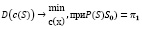(1)
Плотность капитала Фонда выглядит так:
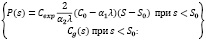
где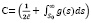 
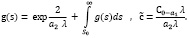
Промежуточное значение:
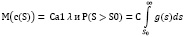
Принимая во внимание то, что
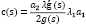
находим:
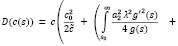
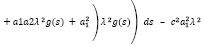
В итоге, возникает данная запись:
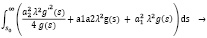
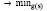
При постоянном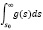 
уравнение Эйлера можно записать следующим образом:
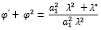(2.1)
где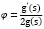 
; λ* – в этом выражении: неопределенный множитель Лагранжа
Следует заметить, что в неравенстве,
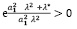
не существует функции g, соответствующей данному уравнению и установленному ограничению.
Зададим:
.
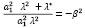Значит решением уравнения (2.1) является (2.2):
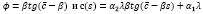
где с̄ – какая-то постоянная величина. Рассматривая политику неизменного управления фондом, найдем с̄ учитывая, что c(s0)=c0: абстрагировавшись от внешних влияний экономики находим:
.
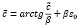В этом варианте максимальная величина капитала Фонда вычисляется:
.
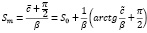Найдем функцию g(s) , учитывая, что g(S0)=1. Получим:
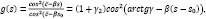
где γ = с̄ / β
Найдем
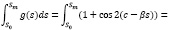
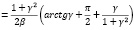
В вариационной задаче связь возникает вследствие:
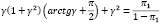(3)
Нетрудно показать, что уравнение (3) имеет единственный положительный корень
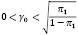
Таким образом, оптимальная скорость выделения средств на социальные программы в случае непрерывного управления
При этом капитал Фонда ни в коем случае не может превышать величины:
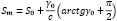
В случае, когда капитал устремляется к наибольшему значению, быстрота выделение ресурсов на социальные расходы критично растет. Абстрагировавшись от требования непрерывности управления капиталом Фонда и найдем постоянную величину с̄ в (2.2)при условии с(S0)=с1. Выражая через
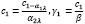
Получим
,
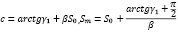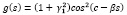
Условие связи в задаче (1) можно записать в виде
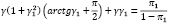
Найдем дисперсию c(s):
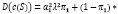
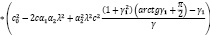
Выразив γ из (4) и подставив в (5), рассмотрим D(c(S)) как функцию параметра γ1, стремясь ее минимизировать. Таким образом, наша задача состоит в минимизации функции
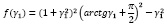
Достаточно легко покажем, что
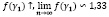
Для того чтобы у1 → ∞ , возьмем с1 < а1λ и далее устремим β к нулю. Найдем
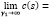
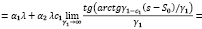
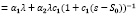
Условие (4) перепишемвтаком виде:
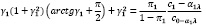
Ищем:
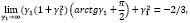
Из чего следует: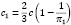 
Таким образом, оптимальная скорость выдачиресурсов на социальные программы будет иметь вид
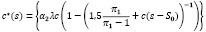
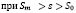, 0 – в противном случае
Максимальная величина капитала фонда рассчитывается по формуле:
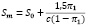
Аналогично при непрерывном управлении и при устремление капитала фонда к максимальному значению быстрота выделения денег на социальные программы неограниченно возрастает.
В итоге, оттолкнувшись от представления о том, что функция управления капиталом фонда непрерывна, мы уменьшили дисперсию c(S) при постоянной вероятности существования выплат по социальным программам, учитывая, что зависимость c(S) от π1 имеет существенно более простой вид. Заметим, что непрерывность c(S) нарушается только при s = S0, где происходит изменение величины
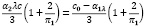
Критический уровень капитала, при принижении которого прекращаются выплаты по социальным программам, найдем из условия фиксации вероятности разорения фонда на любом желаемом уровне α0:
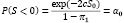
Итак ,искомая конечная функция имеет вид:
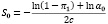
На наш взгляд,вышеизложенная математическая модель в наиболее полной мере способствует организации оптимального функционирования фонда социального страхования.
Библиографическая ссылка
Черкова Т.В., Ермишкина Н.В., Мамаев И.И. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО ФУНКЦИОНИРОВАНИЯ РАБОТЫ ФОНДА СОЦИАЛЬНОГО СТРАХОВАНИЯ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14144 (дата обращения: 21.11.2024).