Теория графов, как и большинство точных наук, возникла из решения и, вернее будет сказать, из формулировки известных математических проблем. В данном случае это задачи о Кенигсбергских мостах, разрезании пиццы и раскраски карты. Все вышеуказанные проблемы связанные, в первую очередь, с некими объектами, имеющими характеристики, представляемые графически, и поэтому естественно применить графы для исследования таких объектов как социальные сети.
Не менее естественно применить для построения, анализа и визуализации по параметрам систему Mathematica 10, которая включает большой набор основных операций на графах, в том числе нахождение путей, циклов, кликов и многое другое. Написаны функции в данной системе для создания специальных семейств графов, генерирование случайных графов и интерактивное построение графов, а также импорт и экспорт в стандартные форматы.
Помимо стандартных функций для работы с графами в системе Mathematica 10 появились функции построения графа по заданным условиям и его анализ.
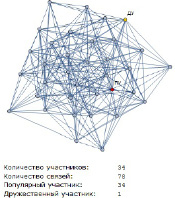
Благодаря мощному встроенному арсеналу функций возможно программирования высокоуровневых задач. Реализована возможность построения графа группы пользователей некой социальной сети по заданным параметрам: общее количество членов сети, количество членов подгруппы, количество связей и пр.
Анализ социальных сетей в сети Интернет ведется не первое десятилетие и поскольку это некая интерпретация социума, есть смысл перенять инструменты изучения из социальных в виртуальные, но с учетом специфики последних.
Оговоримся далее считать «социальными сетями» сообщества реальных людей, а «виртуальные сети» – сообщество аккаунтов на сайте в сети. Вершиной графа сети является аккаунт, а ребром – «дружественная связь между аккаунтами».
Кстати, сам термин «социальная сеть» был введен в 1954 году социологом Джеймсом Барнсом [1] и поскольку при случайно-равномерном соединении вершин графа распределение P(k), (k – число входящих в вершины ребер) является биномиальным, а в пределе большого размера графа – пуассоновским, то такие сети также назвали пуассоновскими случайными сетями и долгое время они были интерпретацией социальных сетей. Тем не менее, в начале XXI века выяснилось, что модель Эрдоса-Реньи плохо коррелируется с реальными графами Интернет-сетей [2].
Значительные результаты последних лет в изучении сетевых Интернет-структур были получены в теоретической физике. В частности, в 1999 г. появилась теория безмасштабных сетей, сформулированная Альбертом-Лассо Барабаши [3]. Безмасштабные сети – это граф, где распределение числа связей вершин описывается степенным, а не экспоненциальным (как в пуассоновских сетях) законом, кроме того, объекты, распределенные по степенному закону, нередко устроены иерархически, а основные свойства сети не зависят от размера сети. Название не было придумано специально для этого типа сетей, а было взято из теории критических явлений.
Исследования показали, что большинство сетей в живой и неживой природе (информационные, экологические, генные, функциональные связи в мозге человека, метаболические, социальные, технологические, словарные, документы WWW и др.) хорошо моделируются безмасштабными графами.
Наиболее интересным объектом для изучения внутри сети является некоторые виды вершин, особенно те, которые регулируют потоки информации, назовем их «дружественными».
Термин «дружественная» – вольный перевод термина Betweenness centrality, который введен еще в 1977 г. социологом Линтон Фриман (American Sociological Association, Vol. 40, No. 1 (Mar., 1977), pp. 35-41).
Математически – это такая вершина, которая имеет самый высокий «индекс дружественности», который рассчитывается как отношение общего количества путей, проходящих через эту вершину к числу минимальных путей, говоря иначе – это вершина, через которую проходит максимальное количество кратчайших путей.
В Mathematica 10 реализован алгоритм вычисления «самой дружественной» вершины любой группы Вконтакте, благодаря которой возможно регулируемое распространения информации.
Библиографическая ссылка
Пастухова Г.В., Казаков В.В. ПРИМЕНЕНИЕ MATHEMATICA 10 ДЛЯ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ ГРАФОВ // Международный студенческий научный вестник. 2015. № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14136 (дата обращения: 05.04.2025).

