Прогнозирование спроса населения на ту или иную продукцию тесно связано с экономическими, социальными, демографическими и научно-техническими аспектами. Платежеспособный спрос населения может принимать разнообразные формы, описание которых происходит с помощью методов математического аппарата.
Например, изучения цен спроса и предложения на какую-либо продукцию или услугу происходит с помощью теории дифференциальных уравнений.
Под дифференциальным уравнением будем понимать уравнение, которое связывает независимую переменную x, неизвестную функцию y и ее производные до некоторого порядка n включительно. Порядком дифференциального уравнения является порядок наивысшей производной.
Одной из моделей, описывающей формирование равновесия и изучающей динамику спроса и предложения на основе теории дифференциальных уравнений, является паутинообразная модель.
Рассмотрим паутинообразную модель с запасами товаров, где от величины запаса зависит скорость изменения цены P. Таким образом: D – спрос, P – цена, S – предложение, равновесная цена и равновесный объем находятся из условия равенства спроса и предложения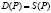 
. Учитывая, что спрос и предложение – линейные функции цены, а именно
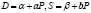
а λ – постоянная, выражающая скорость изменения P при изменении запасов товара, что определяется скоростью реакции, получим дифференциальное уравнение, описывающее процесс изменения цены:
.
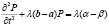В качестве частного решения возьмем постоянную, которая представляет цену равновесия: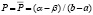 
, тогда отклонение 
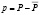удовлетворяет однородному уравнению
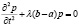
Следующим действием найдем общее значение уравнения. Обозначим в уравнении неизвестную/
Заменим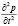 
на k2.
Имеем характеристическое уравнение:
.
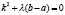Тогда выражение λ(b-a) будет положительным при условии: а<0, b>0, a λ>0.
Если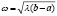 
, тогда характеристическое уравнение имеет корни 
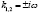. Таким образом, общее решение уравнения будет иметь вид: 
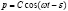, где С и 
– произвольные постоянные, определяющиеся единственным образом, при заданных начальных условиях. Так, добавив 
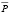, получаем искомый закон изменения цены во времени:
.
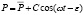Приведем пример. Будем предполагать, что производители зерна определяют предложение S товара в текущем периоде на основе цены p, которая была установлена в предшествующий период. Спрос d на товар изменяется в зависимости от цены в данном периоде.
Таким образом, можно говорить о запаздывании предложения от цены, так как решение об объеме производства принимается с учетом текущих цен, а производственный цикл имеет определенную продолжительность. В связи с этим, предложение, соответствующее данному решению, появится на рынке по окончании этого цикла.
Если спрос и предложения линейно зависят от p, то динамика цены описывается следующими уравнениями:
, 
,
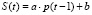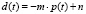которые описывают колебательный характер.
При этом, если
,
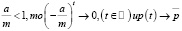последовательность цен сходится к равновесному состоянию.
При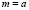 
значения 
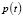чередуются вокруг равновесного значения ¯р.
Если
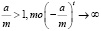
является неустойчивым равновесием. В результате чего бесконечно возрастающих колебаний не наблюдается. Это происходит в связи с тем, что при больших отклонениях от равновесия линейные зависимости спроса и предложения от цены становятся нереалистичными.
Таким образом, паутинообразная модель, показывающая колебания в простейшей динамической модели, в результате которых формируется равновесие. Данная модель отражает формирование равновесия в отрасли с фиксированным циклом производства с помощью дифференциальных уравнений.
Библиографическая ссылка
Галькова А.А., Невидомская И.А. ПРИМЕНЕНИЕ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ПРОГНОЗИРОВАНИИ РАВНОВЕСИЯ СПРОСА И ПРЕДЛОЖЕНИЯ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14120 (дата обращения: 21.11.2024).