Под ранговым распределением (РР) понимается распределение, полученное в результате процедуры ранжирования последовательности значений параметра, поставленных соответственно рангу. Ранг r – это номер особи по порядку в РР. Ранжирование – процедура упорядочения объектов по степени выраженности какого-либо качества в порядке убывания этого качества. Реальные РР могут выражаться различными математическими зависимостями и иметь соответственный графический вид, однако, наиболее важными являются гиперболические ранговые распределения (ГРР), так как они отражают признак «ценозности» – принадлежности совокупности ранжируемых объектов (элементов, особей) к ценозам. Теория ценозов применительно к техническим изделиям была разработана профессором МЭИ Б.И. Кудриным более 30 лет назад (www kudrinbi.ru) и успешно внедрена в практику [1-3]. Методики построения ГРР и их последующее использование в целях оптимизации ценоза составляют основной смысл рангового анализа (РА) (ценологического подхода), содержание и технология которого представляют собой новое направление, сулящее большие практические результаты. Закон гиперболического рангового распределения особей в техноценозе (Н-распределение) имеет вид [1]:
W = A / r β (1)
где W – ранжируемый параметр особей; r – ранговый номер особи (1,2,3….); А – максимальное значение параметра лучшей особи с рангом r =1, т.е. в первой точке; β – ранговый коэффициент, характеризующий степень крутизны кривой РР (для техноценозов 0,5 < β < 1,5 [3]).
Если ранжируется какой-либо параметр ценоза, то РР называется ранговым параметрическим. Подчинённость сообщества особей закону ГРР (1) – главный признак ценоза, но недостаточный. Кроме этого признака, ценозы, в отличие от других сообществ, имеют общую среду обитания, а его объекты включены в борьбу за ресурсы.
В.И. Гнатюком разработан метод РА для оптимизации технических систем-ценозов [3]. Возможности практического использования РА в педагогике описаны Р.В. Гуриной (http://www.gurinarv.ulsu.ru), а также разработана методика его применения в этой области [4]. Количество особей в ценозе определяет мощность популяции. Терминология пришла из биологии, из теории биоценозов. «Ценоз» – это сообщество. Термин биоценоз, введённый Мёбиусом (1877), лёг в основу экологии как науки. Б.И. Кудрин перенес понятия «ценоз», «особь», «популяция», «вид» а из биологии в технику: в технике «особи» – отдельные технические изделия, технические параметры, а многочисленную совокупность технических изделий (особей), РР которых выражается законом (1) называют техноценозом [1-3].
В социальной сфере «особи» – это люди, организованные в социальные группы (классы, учебные группы), тогда мощность популяции – это количество учащихся в группе. Школа – это тоже социоценоз, состоящий из особей – отдельных структурных единиц – классов. Здесь мощность популяции – количество классов в школе. Совокупность школ – это ценоз более крупного масштаба, где особью, структурной единицей данного ценоза является школа. В качестве ранжируемых параметров W в техноценозах выступают технические или физические параметры, характеризующие особь, например, размер, масса, мощность потребления, энергия излучения и т.д. В социоценозах, в частности педагогических ценозах, ранжируемые параметры – это успеваемость, рейтинг в баллах участников олимпиад или тестирования; число учащихся, поступивших в вузы и так далее, а ранжируемыми особями выступают сами учащиеся, классы, учебные группы, школы и так далее.
Исследования последних лет показали, что совокупности космических объектов многих систем (галактики, солнечная система, скопления галактик и т.д.) представляют собой ценозы (космоценозы, астроценозы) [5-8]. Однако, астроценозы отличаются от теноценозов и социоценозов тем, что человек не может влиять на из состояние, изменять и оптимизировать их. В космосе объекты жёстко связаны между собой силами тяготения, определяющими их поведение. Специфика астроценозов до конца не выяснена, метод РА применительно к астроценозам не разработан, что определило цель настоящего исследования. Цель разделилась на ряд задач:
1. Изучение метода РА, выяснение возможности применимости метода РА к астрофизическим системам-ценозам (т.е. в какой мере РА применим к астроценозам).
2. Пошаговое описание применения метода РА для астроценозов.
3. Апробация метода РА применительно к астрофизическим системам.
Метод РА
После изучения методики применения РА для техноценозов [1-3], были выделены её общие (универсальные) элементы, которые распространяются на все виды ценозов. Таким образом, метод РА включает следующие универсальные этапы-процедуры.
1. Выделение ценоза – совокупности объектов изучаемого сообщества (системы).
2. Выделение параметров ранжирования. Такими параметрами могут выступать масса, размеры объектов, стоимость, энергетическая надежность, процентное содержание элемтентов в составе исследуемого объекта, баллы ЕГЭ участников тестирования и т.д.
3. Параметрическое описание ценоза. Создание электронной таблицы (базы данных), содержащей систематизированную информацию о параметрах отдельных особей ценоза.
4. Построение табулированного эмпирического РР. Табулированное РР представляет собой таблицу из двух столбцов: параметров особей W выстроенных по рангу и рангового номера особи r (r = 1,2,3…). Первый ранг имеет особь с максимальным значением параметра, второй ранг имеет особь с наибольшим значением параметра среди остальных особей и т.д.
5. Построение графического эмпирического РР. График эмпирической ранговой кривой имеет вид гиперболы: по оси абсцисс откладывается ранговый номер r , по оси ординат – исследуемый параметр W, рис.1, а. Все данные берутся из табулированного РР.
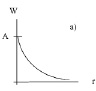
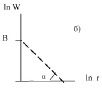
Рис. 1. Гипербола (а) и «спрямленная» гиперболическая зависимость в двойном логарифмическом масштабе (б); В = lnА
6. Аппроксимация эмпирических РР. Аппроксимация и определение параметров РР, как правило, проводится с помощью компьютерных программ, с их помощью задается доверительный интервал, находятся параметры кривой распределения А, В, также определяется коэффициент регрессии Rе (или Rе2 ), показывающий степень приближения эмпирической гиперболы к теоретической. При этом прорисовывается аппроксимационная идеальная кривая (а в случае необходимости – по обе стороны от нее – линии доверительного интервала).
7. Линеаризация ГРР: построение эмпирического РР в логарифмических координатах. Поясним процесс линеаризации зависимости (1). Прологарифмировав зависимость (1) W = А / r β , получаем:
lnW = lnА – β ln r (2)
Обозначив:
lnW = у; lnА = В = const; ln r = х, (3)
получаем (2) в виде:
у = В – β х . (4)
Уравнение (4) – это убывающая линейная функция (рис.1,б). Только по оси ординат откладывается lnW, а по оси абсцисс – lnr. Для построения линейного графика составляется таблица эмпирических значений lnW и lnr, по значениям которой строится график зависимости lnW(lnr) с использованием компьютерных программ.
Вручную коэффициент β определяется по формуле:
β = tg α = lnA : ln r ,
коэффициент А определяется из условия: r = 1, W1= А.
8. Аппроксимация эмпирической зависимости ln W (lnr) к линейной У = В – β х.
Эта процедура производится также с использованием компьютерных программ; далее следует нахождение параметров β, А, определение доверительного интервала, определение коэффициента регрессии Rе (или Rе2), выражающего степень приближения эмпирического графика ln W (ln r) к линейному виду. При этом вырисовывается апроксимационная прямая.
9. Оптимизация ценоза (для био, – техно, – социоценозов).
Процедура оптимизации системы (ценоза) состоит в совместной работе с табулированным и графическим распределениями и сравнении идеальной кривой с реальной, после чего делают вывод: что практически нужно сделать в ценозе, чтобы точки реальной кривой стремились лечь на идеальную кривую. Чем ближе эмпиричекая кривая распределения приближается к идеальной кривой вида (1), тем устойчивее система. Этап оптимизации включает следующие процедуры (действия) [3].
• Теоретическая часть: совместная работа с табулированным и графическим РР:
- нахождение аномальных точек и искажений по графику;
- определение их координат и их идентификация с реальными особями по табулированному распределению;
Практическая часть: работа с реальными объектами ценоза по его улучшению:
- анализ причин аномалий и поиск способов их устранения (управленческих, экономических, производственных и т.д.);
- устранение аномалий в реальном ценозе.
Оптимизация техноценозов по В.И. Гнатюку осуществляется двумя путями [3]:
1. Номенклатурная оптимизация – целенаправленное изменение численности ценоза, устремляющее реальное РР по форме к идеальному (1). В биоценозе-стае это изгнание или уничтожение слабых особей, в учебной группе это отсев неуспевающих, в техноценозе – избавление от хлама, перевод отработанной техники в разряд металлолома.
2. Параметрическая оптимизация – целенаправленное улучшение параметров отдельных особей, приводящее ценоз к более устойчивому, эффективному состоянию. В педагогическом ценозе – учебной группе (классе) – это работа с неуспевающими – улучшение их показателей успеваемости, в техноценозе – замена старой техники улучшенными образцами.
Как указывалось выше, процедура оптимизации 9 неприменима к астроценозам. Изучая их ГРР, можно лишь извлечь ту или иную полезную научную информацию о состоянии астроценоза, тем самым расширив представления об астрономической картине Мира. Каков характер отклонений в реальных ГРР объектов астрофизических ценозов от идеального Н-распределения и на что они указывают? На графиках ГРР объектов систем-астроценозов обнаружены 2 вида искажений:
I. Несколько точек выпадают из доверительного интервала ГРР или гипербола искажена (наличие «горбов», «впадин», «хвостов» (рис. 2, а).
II. Резкий излом логарифмической прямой lnW (lnr), разделяющий её на 2 отрезка (под углом друг к другу или со смещением по оси у).
На рис 2, а, б – графики РР спутников Сатупа с искажениями первого вида.
В силу несовершенства измерительной техники или методов астрономических измерений из всех 62 спутников Сатурна есть сведения о массах 19 спутников и о диаметрах 45 спутников. Из графиков хорошо видно, что в системе с большим количеством особей (рис.2,б) эмпирические точки, отражающие размеры спутников лучше ложатся на логарифмическую прямую., что указывает на более адекватную информацию о полноте системы. Сказанное позволяет утверждать, что применение РА дает возможность прогнозировать наличие недостающих объектов в космических системах.
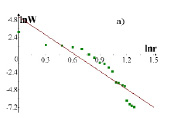
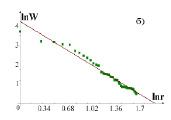
Рис. 2. Ранговое распределение спутников Сатурна в двойном логарифмическом масштабе ln W = f(ln r); r –ранговый номер спутника; а) РР 19 спутников по известным массам; б) РР спутников в той же системе с большим количеством особей – 45 спутников по известным диаметрам
При изучении графических РР астроценозов выяснено, что первый вид искажений может свидетельствовать о том, что:
• некоторые объекты не принадлежат данному астроценозу (системе, классу);
• измерения параметров объектов астроценоза не точны;
• недостаточно сведений о полноте астрофизической системы-ценоза. При этом, чем полнее система, тем больше коэффициент регрессии.
Второй вид искажений свидетельствует о следующем.
Если наблюдается резкий излом на графике спрямления, это означает, что система состоит из двух подсистем. Подобный случай представлен графиками рис. 3, 4. При этом, на графике W (r) острый излом образуется двумя «наползающими друг на друга» гиперболами (рис. 3, а), при этом этот излом не всегда так ярко выражен, как на графике в двойном логарифмическом масштабе (рис.3 б, 4, б). Чем меньше угол между линеаризованными отрезками на графике ln W (ln r), тем более выражен излом гиперболы на графике W (r).
На рис. 3, а, б изображены графики ГРР известных галактик по расстоянию от нашей Солнечной системы (всего 40 объектов).
Если наблюдается резкий излом на графике спрямления, это означает, что система состоит из двух подсистем. РА позволяет теоретически разделить систему галактик на два класса: периферийную (удалённую) группу –1 и местную (близлежащую) группу галактик – 2 , что соответствует астрономическим классификационным данным.
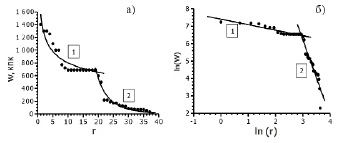
Рис. 3. Ранговое распределение галактик по расстоянию от Солнечной системы, где 1 – периферийная группа галактик, при этом Re=0,97; 2 – местная группа галактик, Re=0,86 ; W – расстояние Галактики, кпк; r – ранговый номер галактики. Всего 40 объектов. а) График W(r), Re=0,97; б) График ln W= f(ln r), Re=0,86
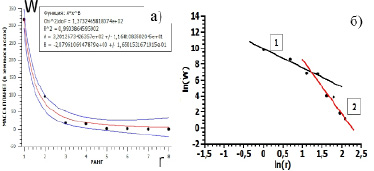
Рис. 4. РР масс планет Солнечной системы (в земных массах), где группа 1 – планеты гиганты (Юпитер, Сатурн, Уран, Нептун); 2 – планеты земной группы; W – масса планеты, М; r – ранговый номер планеты. Всего 8 объектов; а) График W(r), Re= 0,99; б) График ln W= f(ln r), для 1 – (планеты гиганты) Re = 0,86, для 2 также – Re = 0,86
Как известно из курса астрономии в нашей планетной системе выделяется 2 подсистемы: планеты-гиганты и планеты Земной группы. На рис. 4, а, б представлены ГРР планет Солнечной системы по массам. Заметим, что непосредственно на гиперболических РР изломы могут недостаточно явно просматриваться, и на них невозможно выделить подсистемы (рис.4, а), поэтому необходимо обязательное построение РР в двойном логарифмическом масштабе, на которых изломы ярко выражены (рис.4,б).
Используя справочники физических величин и Интернет-ресурс, были выполнены построения ГРР других астроценозов, подтверждающие вышесказанное. Аппроксимация проводилась с помощью программы QtiPlot.
Таким образом:
• рассмотрен и расписан пошагово метод РА для систем-ценозов по аналогии с техноценозами;
• определена специфика применения РА к астроценозам;
• определена возможность применения РА к исследованию астрофизических систем- ценозов в планах:
- идентификации подсистем в космических системах-ценозах; метод заключается в фиксации и изучении изломов линейных графиков ГРР в двойном логарифмическом масштабе;
- прогнозирования полноты астрофизических систем-ценозов;
• требуются дальнейшие исследования в данном направлении, подтверждающие сделанные выводы.
Библиографическая ссылка
Устинова К.А., Козырев Д.А., Гурина Р.В. РАНГОВЫЙ АНАЛИЗ КАК МЕТОД ИССЛЕДОВАНИЯ И ВОЗМОЖНОСТЬ ЕГО ПРИМЕНЕНИЯ К АСТРОФИЗИЧЕСКИМ СИСТЕМАМ // Международный студенческий научный вестник. 2015. № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14114 (дата обращения: 09.04.2025).

