Первая паровая машина в виде так называемого полного параллелограмма Уатта, была запатентована им в 1784г.[1]. Параллелограмм Уатта – есть шарнирный механизм для преобразования прямолинейного движения поршня 8 во вращательное движение кривошипа 1 (рис. 1). По формуле П.Л. Чебышева W = 3n – 2p5, где n число подвижных звеньев, а р5 – одноподвижных кинематических пар пятого класса, подвижность параллелограмма Уатта при n = 8 и p5 = 12 равна нулю, т.е. такой механизм теоретически неподвижен может двигаться лишь с принуждением.
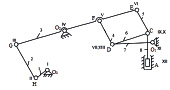
Рис. 1. Кинематическая схема паровой машины Уатта
В 2011году автором настоящей статьи был разработан метод коррекции подвижности плоских кинематический цепей, который был применен к параллелограмму Уатта. После введения дополнительного звена СВ и кинематической пары пятого класса В (рис. 2) подвижность системs стала равной единице.
Рис. 2. Кинематическая схема полного параллелограмма Уатта с дополнительным шатуном
Такой исправленный механизм был заявлен в 2013 году в Роспатент под названием «Полный параллелограмм Уатта с дополнительным шатуном». В 2014 году по предложенной схеме был выдан патент на изобретение [2].
Проведем кинематический анализ полного параллелограмма Уатта с дополнительным шатуном графо-аналитическим методом, т.е. построим план скоростей (рис. 3), задавшись движением кривошипа ОЗН, (VН). При этом скорость точки G (VG) относительно неподвижной стойки О2 определится из уравнений,
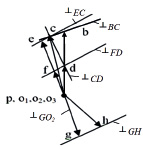
Рис. 3. План скоростей
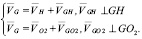
Скорости точек F и E определятся по свойству подобия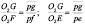 
, т.е. они пер пендикулярны О2G и равны 
.
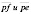Далее становится возможным найти скорости точек D, C и B.
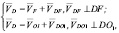
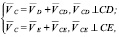
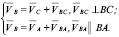
Таким образом, усовершенствованный полный параллелограмм Уатта имеет вполне корректное кинематическое разрешение. Решение этой задачи от поршня А к кривошипу ОЗН оказывается более сложным, однако оно существует, т.к. имеется доказательство обратного решения от ОЗН.
Библиографическая ссылка
Ковалева М.П. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПОЛНОГО ПАРАЛЛЕЛОГРАММА УАТТА С ДОПОЛНИТЕЛЬНЫМ ШАТУНОМ // Международный студенческий научный вестник. – 2015. – № 5-5. ;URL: https://eduherald.ru/ru/article/view?id=14065 (дата обращения: 21.12.2024).