Существующие в настоящее время математические модели вычислительных систем (ВС) не пригодны для исследования ВС с виртуализацией, из-за отсутствия возможности комплексно рассматривать не только потоки информации внутри модели, но и учитывать при этом изменения конфигурации самой модели в зависимости от случайных факторов – программно-аппаратных сбоев, так и заданных схем реконфигурирования системы, что характерно для ВС с виртуализацией.
К современным ВС и системам хранения предъявляются высокие требования:
- адаптируемость к быстро меняющимся задачам;
- гарантия заданного уровня производительности приложений;
- обеспечение требуемого уровня масштабируемости;
- простота эксплуатации и обслуживания;
- стоимость владения должна быть минимизирована.
Наиболее эффективным путем удовлетворения перечисленных требований является использование ВС с виртуализацией. Создание, верификация и анализ возможностей применения математических моделей ВС с виртуализацией ресурсов в образовательном процессе в качестве доступного инструмента для исследования ВС с виртуализацией, а также применения их реализаций – виртуальных серверов на практике, обуславливает актуальность и практическую ценность проводимого исследования.
Анализ публикаций показывает, что в мировой и отечественной практике для решения задач проектирования зачастую используются аналитические методы, требующие для своей реализации меньше вычислительных ресурсов и позволяющие решать как задачи анализа, так и задачи оптимизации параметров [3]. Причем получаемые средние значения характеристик модели, обычно не более чем на 10-15% отличаются от реальных, что вполне приемлемо при инженерных исследованиях.
В представленной работе для расчетов используется метод замкнутых стохастических систем массового обслуживания (СМО), математический аппарат которого уже разработан, но рассчитан на моделях с фиксированными параметрами [2]. В моделях ВС с виртуализацией необходимо учитывать возможность распределения процессорной мощности физического процессора, начиная от 10% с шагом в 1% прямо во время работы [4], см. рис. 1. Поэтому метод был адаптирован для задания и изменения числа каналов обслуживания в СМО в виде доли мощности канала обработки. В том случае, если заданное число каналов в СМО равно 1 – при расчете такая СМО считается одноканальной, иначе многоканальной.
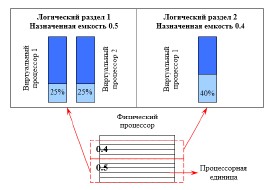
Рис. 1. Разделение процессорной мощности
Из-за модификации метода, потребовалось вычислять выражения со степенью с дробным показателем и дробным факториалом, для этого ряд формул был заменен на вычисления приближенных значений. Так, например, вычисление факториала заменено формулой Стирлинга [6], что позволило применить существующий метод расчета для моделей ВС с виртуализацией.
В рамках данного исследования в моделях предполагается наличие пула свободных ресурсов или пула виртуальных серверов – доноров, поскольку моделируется один виртуальный сервер в каждом случае, а не хост-платформа целиком.
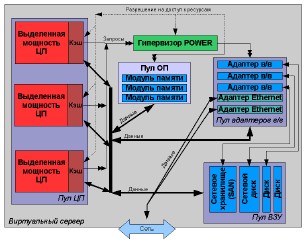
Рис. 2. Структурная схема виртуального сервера
Для реализации свойств адаптивности в моделях были использованы триггеры, которые отслеживают и корректируют мощность канала обработки в отдельно взятых СМО в зависимости от заданных условий [1], которые задаются непосредственно перед расчетом модели, путем назначения диапазона изменений и события срабатывания. В реальных ВС тот же самый функционал обеспечивается заданием политики управления ресурсами для менеджера управления ресурсами (PLM), см. рис. 3.
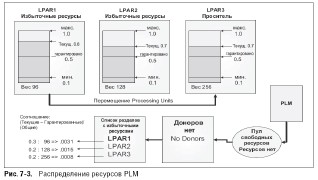
Рис. 3. Распределение ресурсов PLM
Также в модели задается вероятность сбоя в виде триггера псевдослучайных сбоев, который создает события времени выполнения модели и позволяет моделировать отказ тех или иных устройств в модели ВС. Эти события проявляются, как резкое сокращение мощности канала обработки в какой-либо СМО до минимального значения равного 0,1. Совсем исключить СМО, в которой произошел сбой, из модели не представляется возможным, поскольку это влечет за собой изменение размера матрицы передач, что в свою очередь исказит всю собранную до момента сбоя статистическую информацию. Для абстрагирования от привязки и измерения количества тактов процессоров для выполнения той или иной задачи, в моделях используются условные единицы времени обслуживания, задаваемые при расчетах, с учетом экспериментально полученных данных о времени обработки заявки с заданной трудоемкостью.
Отличительной особенностью разработанных моделей является возможность задания ресурсов в процентном соотношении. Адаптивные модели выгодны еще и тем, что в процессе выработки решения об изменении конфигурации используется информация, поступающая как от самой модели, так и от исследователя, в виде схем принятия решения [5]. В ходе исследования были получены простые и легко изменяемые модели для анализа. Число заявок в модели равное 8 и 16 было выбрано экспериментальным путем, исходя из количества СМО в моделях, а также времени расчета модели.
Пример зависимости коэффициента загрузки от числа заявок в модели показан на рис. 4.

Рис. 4. Динамика коэффициента загрузки от роста числа заявок
Оптимизировать модели можно по следующим параметрам:
1) коэффициент загрузки, который показывает эффективность использования ресурса;
2) среднее время пребывания заявки в сети, поскольку, справедливо считать, что чем производительнее система, тем меньше среднее время пребывания заявки в сети или тем меньше время реакции ВС на запрос.
В ходе экспериментов с моделями было выявлено, что для оптимизации – минимизации среднего времени пребывания заявки в сети, необходимо временно увеличить выделенную процессорную мощность до 3,36. При этом коэффициент загрузки процессоров снижается, поскольку заявки начинают обрабатываться параллельно. Соответственно после обработки ресурсы могут быть возвращены обратно в пул свободных ресурсов. С помощью варьирования параметров ЦП, ОП и других компонентов модели, были получены следующие графики динамики коэффициента загрузки как отдельно по СМО, так средней по модели, см. рис. 5 а и 5 б.

Рис. 5 а

Рис. 5 б
На графиках видно влияние доступности дополнительных ресурсов ЦП: при изначально высокой доступности ресурсов снижаются временные затраты на обработку заявок, но при этом также уменьшается эффективность использования этих ресурсов. Таким образом, результаты исследования свидетельствуют о том, что оптимизация «на лету» при наличии пула свободных виртуальных ресурсов, позволяет наиболее эффективно решать задачу, возложенную на ВС, так и наиболее эффективно использовать аппаратные ресурсы, при условии их аренды в ситуациях с пиковой загрузкой, тем самым позволяет снизить общие затраты на аппаратные ресурсы.
Верификация моделей является важным этапом и была выполнена экспериментально, путем создания виртуального сервера на хост-платформе IBM System P и измерением его динамических характеристик. Для генерации нагрузки на сервере, другими словами имитации выполнения заявок по аналогии с моделями, использовалась утилита Stress. Для сбора статистики о работе виртуального сервера использовалась утилита NMON.
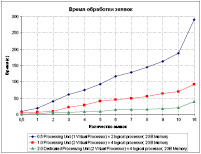
Рис. 6. Время обработки заявок
Максимальный результат по скорости обработки заявок достигается, когда число виртуальных процессоров равняется числу потоков в программе или заявке. Средняя скорость обработки заявок соответственно по трем конфигурациям равняется: 0,053, 0,141, 0,483 (заявок/сек). Сравнение результатов показывает схожее поведение модели и реальной системы, как по характеристикам загрузки, так и по использованию ресурсов, а также наглядно продемонстрировала эффект адаптивности к нагрузке, что в свою очередь свидетельствует о корректности использования разработанных моделей для изучения и моделирования ВС с виртуализацией. При этом есть и некоторые различия, которые объясняются различием в распределении входного потока заявок в моделях или пакета задач в реальной системе.
Результатами проведенных исследований являются:
1) Способ адаптации математического аппарата теории массового обслуживания для расчета моделей ВС с виртуализацией, который позволяет использовать проверенный временем математический аппарат с небольшой модификацией для совершенно другого типа ВС.
2) Тестовые модели ВС для различного вида нагрузок, которые были верифицированы экспериментальным путем, что позволило наглядно показать одинаковую динамику модели и виртуального сервера и доказать достоверность моделей.
3) Проведен анализ возможностей применения разработанных моделей и их реализаций – виртуальных серверов, что освещает важный аспект применения полученных результатов на практике и указывает возможные пути дальнейшего развития по теме моделирования в области виртуализации, в связи с выявленными недостатками технологии.
С практической точки зрения, реализацией моделей являются виртуальные сервера, которые во многих случаях гораздо удобнее использовать, нежели традиционные полностью аппаратные решения.
Библиографическая ссылка
Валова О.О., Мартышкин А.И. РАЗРАБОТКА И ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ С ВИРТУАЛИЗАЦИЕЙ // Международный студенческий научный вестник. 2015. № 3-2. ;URL: https://eduherald.ru/ru/article/view?id=12472 (дата обращения: 06.04.2025).

